Solutii In Elemente de contur

2.5.1. Metoda elementelor de contur.Principii de baza.Metoda directa.

Formularea directa si indirecta a metodei elementelor de contur este ilustrata pentru ecuatiile diferentiale cu derivate partiale de tip Poisson, Laplace si Helmholtz din cauza simplitatii aplicarii. De altfel aceste ecuatii au multiple aplicatii in practica inginereasca: problemele de potential (campul de temperatura, curgerea fluidelor, electrostatica si mecanica solidelor deformabile, torsiunea) si propagarea undelor.

Tehnica de rezolvare consta in transformarea ecuatiilor cu derivate partiale, ce descriu comportarea campului necunoscut in interiorul si pe frontiera domeniului, intr-o ecuatie integrala numai cu valori pe contur care este in continuare discretizata. Valorile in punctele interioare domeniului se determina plecand de la valorile de pe contur. Deoarece toate aproximatiile numerice sant efectuate numai pe contur, dimensiunea problemei este redusa cu o unitate, sistemul de ecuatii algebrice obtinut fiind de o dimensiune mult mai redusa decat cel rezultat din alte metode numerice: metoda elementelor finite, a diferentelor finite, etc.

Fie domeniul cu conturul S divizat in si .

Se considera ecuatia Poisson

in , (2.5.1.1)

cu conditile de contur:

pe , pe (2.5.1.2)

Pentru problema pusa, se scrie ecuatia rezidului ponderat,

(2.5.1.3)

Integrand prin parti de doua ori expresia (2.5.3), rezulta ecuatia itegrala de contur:

(2.5.1.4)

Formularea directa a metodei elementelor de contur consta in utilizarea functiei pondere w, in ecuatia (2.5.1.4) a solutieei fundamentale a ecuatiei Laplace, ,

(2.5.1.5)

fiind functia delta Dirac, fiind potentialul in punctul x corespunzator unui potential unitar aplicat in punctul .

Introducand in (2.5.1.4), pentru un punct apartinand domeniului , (fig. 2.5.1.1) se obtine:

care, tinand cont de proprietatea de filtrare a functiei Dirac, se transforma in:

(2.5.1.6)

Ecuatia integrala (2.5.1.6) leaga potentialul in punctul de valorile functiilor u si q de pe contrur. Pentru un domeniu izotop, solutia fundamentala a ecuatiei (2.5.1.5) este : v.fig.(2.5.1.1)

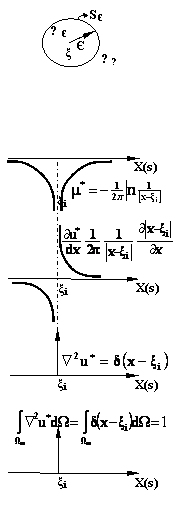
bidimensional

tridimensional, in care este distanta dintre punctele de observatie x si de aplicare a potentialului unitar

Solutiile (2.5.1.7) satisfac identic ecuatia (2.5.1.5), scrisa, respectiv, in coordonate polare si sferice, in orice punct, cu exceptia cazului unde solutia fundamentala este singulara, figura 2.5.1.2. In acest punct, se demonstreaza cu teorema de divergenta (fig. 2.5.1.1)

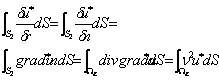
ca:

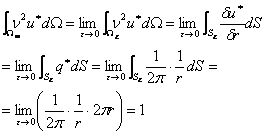
Sunt posibile urmatoarele trei localizari ale potentialului unitar:

-interior domeniului-

-exterior domeniului -S

-pe contur-

Pentru interior domeniului este valabila ecuatia (2.5.1.6) iar pentru exterior domeniului, relatia (2.5.1.6) se poate scrie:

(2.5.1.8)

ecuatie care nu reprezinta nuclee singulare. In virtutea alegerii punctelor de actionare a potentialului unitar, ecuatia matriceala rezultata ca urmare a discretizarii ecuatiei integrale (2.5.1.8) poate sa nu aiba o diagonala dominatasi deci devine dificila in rezolvare. De asemenea nu este evidenta nici o posibila alegere optima a pozitiei punctelor .

Pentru localizat pe contur, ecuatia (2.5.1.6) se scrie:

(2.5.1.9)

unde este un coeficient care depinde de forma conturului pe care este situat . Coeficientul c se poate determina cu expresia (2.5.1.6) , facand ca sa tinda spre conturul S. Se considera, astfel, punctul drept centrul unui cerc a carui raza tinde spre zero (fig 2.5.1.3,a).

Rezulta :

Daca se considera cele doua situatii posibile: se obtine acelasi rezultat. Daca, de exemplu :, apartine partii de contur , atunci, prima integrala a membrului doi din ecuatia (2.5.1.6) are forma:

(2.5.1.2.5)

Prin trecere la limita si considerand un contur regulat, neted, ,si

Interpretarea geometrica a acestei treceri la limita este ilustrata in figura (2.5.1.3,b).

In aceste conditii relatia (2.5.1.2.5) devine:

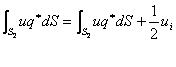(2.5.1.11)

Pentru a doua integrala din primul membru al expresiei (2.5.1.6), limita este:

astfel ca pentru o portiune de contur

(2.5.1.12)

Prin luarea in consideratie a ecuatiilor (2.5.1.11) si (2.5.1.12), ecuatia (2.5.1.6) pentru punctul situat pe un contur regulat, neteted, are forma urmatoare:

Daca in conturul nu este regulat, coeficientul va avea diferite valori depinzind de procesul de trecere la limita descris (in cazul din fig 2.5.1.4, ).

Rezumand cele expuse, ecuatia integrala pe contur are forma :

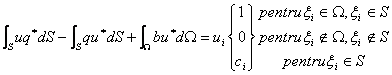(2.5.1.14)

2.5.2.Metoda indirecta.

Ecuatia Poison (2.5.1.11) impreuna cu conditiile de contur (2.5.1.2) se rezolva cu metoda indirecta, cand se distribuie pe contur valorile lui (distribuite de surse) sau de(distributie de dipoli) cu o densitate nedeterminata. Aceste distributii satisfac conditiile de contur.

Formulareaindirecta se stabileste plecand de la formulare directa ce se refera atat la problema interioara cat si la cea exterioara. Pentru aceasta, in afara domeniului se considera si domeniul complementar, (fig. 2.5.2.1).

Se defineste an problema interioara cu variabila u si in . Problema exterioara cu variabila . Pentru problema interioara sant valabile ecuatiile (2.5.1.14). Pentru problema exterioara se tine seama ca normala este diriijata spre interiorul lui , astfel incat se scriu urmatoarele ecuatii:

(2.5.2.1)

Prin substituirea relatiei (2.5.2.1) in (2.5.1.14) pentru , se obtine:

(2.5.2.2)

Se impune pentru cele doua variabile u si pe conturul S conditia si se introduce substitutia . Ecuatia (2.5.2.2) ia forma:

(2.5.2.3)

unde este densitatea de distributie necunoscuta a lui u pe contur.

Daca se procedeaza ca si in cazul expresiei (2.5.2.1), punctul tinde spre conturul S.

Potentialul unitar, u, se determina cu relatia (2.5.2.3), in timp ce se obtine printr-un proces de trecere la limita:

(2.5.2.4)

Ecuatiile (2.5.2.3) definesc o formulare sursa, indirecta. Pentru determinarea lui se impun conditiile de cuntur,

pe

si pe .

Cunoscand , potentialul in punctele interioare se calculeaza cu ajutorul expresiei(2.5.2.4). Ca o alternativa la conditia pe contur, se poate pune conditia deechilibru, Se introduce notatia

si din relatia (2.5.2.1) rezulta ecuatia:

(2.5.2.5)

in care sete densitatea de distributie necunoscuta a lui .

Analog cazului precedent, cand punctul tinde spre , in integrala pe S din formula (2.5.2.5) apare un moment singular care inlaturat, se obtine:

Derivata pe directie normala la frontiera, este:

(2.5.2.7)

Ecuatiile (2.5.2.6) si (2.5.2.7) definesc formularea (dipol) indirecta.

Densitatea se determina prin impunerea conditiilor pe contur,

pe ,

pe ,

cunoscand , potentialul in punctele interioare se caalculeaza din expresia (2.5.2.6).

2.5.3.Discretizarea ecuatiilor integrale pe contur.

Pentru rezolvarea numerica a ecuatiilor integrale pe contur se discretizeaza conturul in elemente finite, segmente de dreapta sau curbe, denumite elemente de contur. Se utilizeaza elemente de contur constante, liniare, patratice, de ordin superior, izoparametrice. Puntele unde se considera valorile necunoscute se numesc noduri. In fig. 2.5.3.1 este reprezentat modul de discretizare a conturului unui domeniu plan cu diferite tipuri de elemente de contur iar in fig. 2.5.3.2 - diferite moduri de variatii ale functiilor de interpolare pentru elementele de contur in cazurile bidimensional si tridimensional.

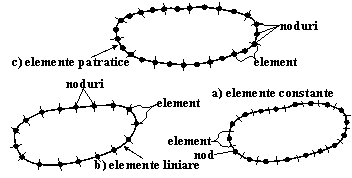Fig.2.5.3.1

2.5.3.1.Elemente de contur constante.

Pentru acest tip de elemente de contur, nodurile sunt considerate in mijlocul fiecarui segment. Conturul este discretizat in N elemente din care sunt considerate apartinand portiunii iar portiunii lui .

In ecuatiile integrale pe contur(2.5.1.14), se considera ca valorile lui u si q sunt constante pe fiecare element si egale cu valorile lor in nodul din mijloc. In fiecare element valoarea uneia dintre cele doua variabile, u sauq este cunoscuta si se admite soluaia ecuatiei Laplace (). Sollutia fundamentala (potentialul unitar) este aplicat in si , respectiv, rezulta .

Pentru simplificarea notatiilor, nu se mai scrie.

Fig.2.5.3.3

Ecuatia (2.5.1.14) discretizata are forma

(2.5.3.1)

fiind lungimea elementului j. Ecuatia (2.5.3.1) reprezinta relatia dintre nodul i in care se aplica solutia fundamentala (potentialul unitar) si toate elementele j (inclusiv cele pentru care i=j) de pe contur (fig. 2.5.3.3). cum valorile lui u si q sunt constante pe fiecare element, ele pot fi scoase in afara integralelor din ecuatia (2.5.22), obtinandu-se :

Integralele leaga nodul i cu elementul j pe care se calaculeaza.

Aceste integrale se noteaza . Similar, integralele sunt denumite .

Ecuatia (2.5.3.2) se rescrie:  (2.5.3.3)

In cazul in care se defineste   (2.5.3.4)

Ecuatia (2.5.3.3) ia forma :  (2.5.3.5)

sau, in forma matriceala: . (2.5.3.6)

Cele N, valori ale lui u si valori ale lui q sunt necunoscute pentru S.

Rezulta un sistem algebric cu N necunoscute, care se ordoneaza n mod corespunzator, obtinandu-se forma canonica (2.5.3.7)

In expresia (2.5.3.7), este vectorul necunoscutelor corespunzatoare lui u si q, in membrul secund fiind marimile cunoscute ale potentialului si fluxului.

Dupa rezolvarea sistemului (2.5.3.7) toate valorile poentialului si fluxului q pe contur sunt cunoscute, valorile lor an punctele interioare domeniului, determinandu-se cu relatia (2.5.1.14)-fig. 2.5.3.4- care, in forma discretizata, este:

Marimile fluxurilor interne se calculeaza prin derivarea ecuatiiei (2.5.1.14):

in care sunt coordonatele , e=1,2 pentru probleme tratate in spatiul bidimensional, e=1,2,3 pentru cele tratate in spatiul tridimensional.

Inegralele si se pot calcula utilizand cuadratura sau cubatura GAUSS simpla pentru toate elementele (exceptand cazul cand potentialul unitar actioneaza pe elementul de contur care se considera, i=j :

unde este lungimea elementului iar este ponderea asociata integrarii numerice in punctul k. Functiile si sunt evaluate in acelasi punct.

Lungimea este divizata la doi deoarece formulele de integrare numerica sunt date in mod obisnuit pentru intervalul .

Sunt suficiente patru puncte de integrare Gauss pentru a obtine precizia ceruta in probleme bidimensionale. Integralele corespunzatoare elementelor singulare se calculeza cu cuadraturi de ordin superior.

In cazul particular al elementelor de contur constante, integralele si pot fi calculate analitic.

De exemplu, termenul este identic nul din cauza ortogonalitatii dintre normala la element si contur,

Formularea indirecta (sursa) se poate deasemenea exprima in forma matriceala plecand de la ecuatiile (2.5.2.6) si (2.5.2.7).

Discretizand conturul in elemente se obtine:

(2.5.3.2.5)

Diferenta dintre aceasta formulare si cea directa este acea ca matricile G si H sunt necuplate iar termenii diagonali ai lui H sunt in loc de . Ecuatiile (2.5.3.2.5) se mai pot scrie:

(2.5.3.11)

Ecuatiile (2.5.3.11) se aplica tuturor punctelor de pe contur cu conditiile:

in puncte pe in puncte pe .

Sistemul final de ecuatii este:

in care necunoscutele cuprinse in vectorul sunt intensitatiile sursa.

2.5.3.2.Elemente de contur liniare.

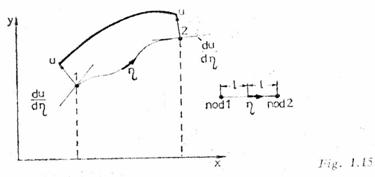
In acest caz nodurile sunt luate in punctele de intersectie a elementelor, iar u si q au o variatie linara pe elementul de contur (fig. 2.5.3.5) . Valorile lui u si q intr-un punct oarecere al elementului depind liniar de valorile modale si de doua functii de interpolare liniare,

(2.5.3.12)

Cordonata adimensionala este egala cu iar functiile si sunt date de expresiile: (2.5.3.13)

Se considera din nou ecuatiia integrala pe contur (2.5.1.14). Integrala pe elementul de contur, segment de dreapta, j, din membrul stang al ecuatiei (2.5.14) se scrie :

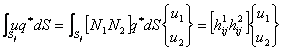(2.5.3.14)

unde:

Coeficientii de influenta definesc interactiunea dintre punctul i considerat si nodul k al elementului j. Integrala din membrul drept al ecuatiei (2.5.1.14) se exprima sub forma:

unde

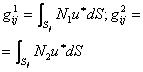
Fig.2.5.3.5

Pentru a scrie ecuatia discreta corespunzatoare nodului i se insumeaza contributiile celor doua elemente de contur alaturate, (j-1) si j, intr-un singur termen, definandu-se astfel coeficientul nodal.

Rezulta ecuatia: . (2.5.3.16)

unde fiecare termen este egal cu teermenul al termenului j-1 insumat cu termenul al elementului j pentru o numerotare orara.

In mod asemanator se procedeaza pentru .

In fig. 2.5.3.5 se stabilesc elementele geometrice necesare pentru calculul coeficientilor din (2.5.3.14) si (2.5.3.15).

Cand punctul de observatie apartine elementului de contur pe care se efectueaza integrarea, coeficientul,

El este nul intotdeauna deoarece:.

Coeficientii din (2.5.3.15) se pot obtine sub forma analitica. Totusi trebuie considerate urmatoarele cazuri limita:

-punctul de observatie coincide cu nodul 1 al elementului de contur, fig. 2.5.3.6. In acest caz rezulta:

-punctul de observatie coincide cu nodul 2 al elementului de contur (fig. 2.5.3.6).

In acest caz se obtin relatiile:

Pentru elemente de contur care nu contin punctul de observatie, integralele care dau coeficientii de influenta sunt (cu notatiile geometrice din fig. 2.5.3.5)

2.5.3.3.Elemente de contur patratice si de ordin superior.

Aceste tipuri de elemente sunt frecvent utilizate pentru reprezentarea mai buna a geometriei corpului. Ele nu prezinta dificultati deosebite in calcul, dar pentru aplicarea lor este necesara transformarea coordonatelor carteziene in cele curbilinii. Se considera conturul curb din fig. 2.5.3.5 si elementul de contur din fig. 2.5.3.7 functiile u si q se exprima, in functie de coordonata astfel:

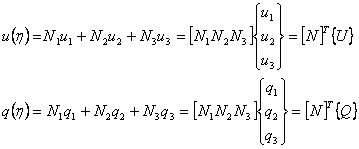(2.5.3.17)

unde

Integralele pe un element j sunt similare celor din cazul elementului de contur liniar.

Astfel,integrala marimii u este:

(2.5.3.19)

si similar pentru q. Evaluarea integralelor cere utilizarea jacobianului deoarece N, sunt functii de si integralele sunt luate pe conturul S.

Pentru o problema bidimensionala, jacobianul este: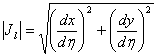 (2.5.3.20)

si (2.5.3.21)

Substituind (2.5.3.21) in (2.5.3.19) se obtine integrala: .

Care se calculeaza numeric.

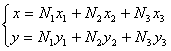
Consideratii similare sunt valabile si pentru integralele referitoare la q. Pentru calculul transformarii (2.5.3.20) trebuie sa se exprime variatiile coordonatelor x si y pe contur in functie de . Pentru elementele de contur izoparametrice ele sunt scrise in acelasi fel ca pentru u si q (geometria si variatia functiilor de interpolare este aceeasi

,

si fiind coordonatele nodului in sistemul global.

Se pot considera de asemenea si elemente de contur de ordin superior.

De exemplu, se poate obtine o variatie cubica pentru u si q considerand patru noduri pe element (fig. 2.5.3.8).

In acest caz:

(2.5.3.22)

unde

Se poate de asemenea defini variatia cubica a functiei u (in acelasi mod fiind considerata si pentru q si coordonatele x si y) luand drept necunoscute functia si derivatele ei in cele doua noduri extreme (fig. 2.5.3.9)

Astfel,

si

Metoda Reciprocitatilor.

2.5.4.1. Metoda Reciprocitatilor .

In formulare directa pentru ecuatia Poisson din (2.5.1.1), in afara integralelor pe contur exista si integrala pe domeniu,

(2.5.4.1)

Pentru rezolvarea acesteia exista maai multe posibilitati. Una dintre ele consta in divizarea domeniului in elemente finite, denumite si celule in metoda elementelor de contur, reteaua lor fiind mult mai rara decat metoda propriu-zisa a elementelor finite (fig 2.5.4.1).

Integrala numerica are forma :

in care sunt ponderi de integrale, iar functia este evaluata in cele k puncte de integrare, N, este numarul de elemente finite in care domeniul 1 a fost divizat iar - suprafata fiecaruia dintre ele, b, fiind valabila pentru fiecare pozitie a solutiei fundamentale in i. Sistemul de ecuatii pentru N noduri, in forma matriceala, este:

(2.5.4.3)

valori ala ale lui u si valori ale lui q fiind cunoscute pe contur.

Ecuatia (2.5.4.3) se poate aduce la forma canonica (2.5.3.8). Dupa ce valorile lui u si q au fost determinate pe contur, se poate calcula u in orice punct din interiorul domeniului cu relatia:

O alta cale de rezolvare a integralei pe domeniul (2.5.4.1) este transformarea acesteia intr-o integrala pe contur a unei functii b armonice in, folosind a doua formula a lui GREEN.

A treia posibilitate este cea oferita de metoda reciprocitatii duale si metoda reciprocitatii multiple.

2.5.4.2. Metoda Reciprocitatii Duale. (MRD)

Aceasta metoda (MRD) a fost introdusa de Nardini si Brebbia pentru rezolvarea problemelor de elasto-dinamica. Ea reprezinta o cale generalizata de constructie a solutiilor particulare si este utilizata pentru considerarea fortelor mastice, pentru probleme neliniare si tranzitorii-hiperbolice si parabolice.

In metoda reciprocitatii duale se considera ca functia b poate fi scrisa sub forma:

(2.5.4.5)

in care sunt coeficienti numerici necunoscuti, j sunt diferite puncte de pe contur sau din domeniu denumite "poli".

Functiile sunt de acelasi tip pentru toate aceste puncte. Se defineste solutia particulara corespunzatoare functiei de exemplu:

(2.5.4.6)

se obtine prin derivarea solutiei particulare in ipotezele de mai sus, ecuatia (2.5.1.14) ia forma:

(2.5.4.7)

fiecare termen din membrul drept al ecuatiei se integreaza prin parti obtinand numai integrale de contur (fiecare termen j implica o solutie particulara localizata in polul j) si expresia (2.5.4.7) ia forma:

Aceasta relatie contine numai integrale de contur dar in membrul drept exista un sir de termeni, fiecare dintre ei reprezentand efectul solutiei particulare localizata in polul j. Dupa discretizarea obisnuita in metoda elementelor de contur a ecuatiei (2.5.4.8), rezulta sistemul:

sau

unde

sunt matrici (M este numarul de puncte in care functia j a fost aplicata, N - numarul obisnuit de necunoscute pe contur iar L - numarul de puncte interioare, M=N + L). Coloanele acestor matrici reprezinta valorile functiilor u si q in diferite noduri, in cazul cand functia actiomeaza intr-un nod j. Coficientii sunt in relatie cu valorile functiei in punctele considerate prin (2.5.4.11)

in care este o matrice , inversabila iar - un vector care include marimile functiei in poli, ale carei elemente sunt valorile in toate punctele pentru fiecare pozitie j a functiei f. Din relatia (2.5.4.11) se obtine:

Se poate scrie (2.5.4.9) in forma:

(2.5.4.12)

Matricele sunt functii de geometria problemei pozitia nodurilor si polilor, tipul de interpolare, iar solutiile particulare.

Cea mai importanta problema in metoda reciprocitatii duale este alegerea functiilor de interpolare . Dupa o serie de experimente numerice, Brebbia si Nadini au propus folosirea functiilor "conice" de tipul distantei intre punctele de aplicatie ale functiei si un punct dat, x:

Acesta conduce la o functie pentru operatorul Laplace de forma:

In plus, acesti autori recomanda adaugarea unei constante alese corespunzator pentru completitudine. Aceasta poate fi inclusa prin functia care conduce la urmatoarea solutie particulara pentru ecuatia Laplace .

Pentru probleme axial simetrice Wrobel, Brebbia si Telles au propus functia:

in care este dinstanta de la diferiti poli la axa de revolutie iar R - distanta de la un punct de pe S la aceeasi axa.

Functiile sunt de acelasi tip ca si pentru analiza tridimensionala.

2.5.4.3.Metoda Reciprocitatii Multiple.

Metoda reciprocitatii multiple este o noua metoda pentru transformarea integralelor de domeniul in integrale pe contur. Are urmatoarele carecteristici care sand similare cu metoda reciprocitatii duale, insa in loc de a aproxima termenul sursa printr-un sir de functii de coordonate se introduce un sir de functii depinzand de solutiile fundamentale. Acest sir cuprinde un sistem de solutii fundamentale de ordin superior care permit aplicarea identitatii lui Green fiecarui termen al sirului. Ca rezultat, metoda conduce la limita la formarea exacta pe contur a problemei.

Se consideri din nou cazil ecuatiei Poisson (2.5.1.1). Integrala pe domeniu (2.5.4.1) se transforma intr-o serie de integrale echivalente de contur. Pentru aceasta se introduce o noua functie legata de solutia fundamentala u* a ecuatiei Laplace (2.5.1.5) prin formula:

Integrala pe domeniu (2.5.4.1) se exprima prin formula:

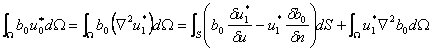(2.5.4.13)

cum functia sursa este cunoscuta, se poate obtine analitic si deci se poate defini o noua functie.

Integrala de domeniu in membrul drept al relatiei (2.5.4.13) poate fi scrisa intr-o forma similara dezvoltarii precedente:

Se poate acum calcula o functie astfel incat:

si procedeul continua.

Astfel, procedeul poate fi generalizat prin introducerea a doua siruri de functii definite prin urmatoarea formula de recurenta:

(2.5.4.14)

Integrala de domeniu se exprima astfel:

(2.5.4.15)

Introduncand (2.5.4.14) in (2.5.4.1) se obtine o ecuatie integrala cu valori numai pe contur:

In forma discretizata expresia (2.5.4.16) are forma:

(2.5.4.17)

unde in afara matricelor obisnuite de influenta notate aici cu si apar matricele din folosirea solutiilor fundamentale de ordin superior. Vectorii contin functia si derivatele ei in raport cu normala in nodurile de pe contur. S-a demonstrat convergenta rapida a seriei intr-un mare numar de cazuri practice.

In cazul cand operatorul Laplace este scris in coordonate cilindrice, functia are forma:

r fiind dinstanta dintre puncte. Coeficientii se obtin din urmatoarele relatii de recurenta:

Pentru j=0 rezulta solutia fundamentala clasica .