3.1. Definitie. Fie sirul de numere
reale ![]() si sirul
sumelor partiale
si sirul
sumelor partiale
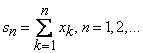
Perechea ![]() se numeste serie
de numere reale si se noteaza
se numeste serie
de numere reale si se noteaza
![]() sau
sau ![]() sau
sau ![]() (1)
(1)
Termenii sirului ![]() se numesc termenii seriei
se numesc termenii seriei ![]() ,
iar
,
iar ![]() se numeste termenul
general al acestei serii.
se numeste termenul
general al acestei serii.
a)
Daca sirul ![]() are limita
are limita ![]() (finita), vom scrie
(finita), vom scrie
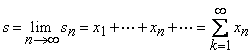 (2)
(2)
si spunem ca seria ![]() este convergenta
avand suma egala cu
este convergenta
avand suma egala cu ![]() ,
in caz contrar, seria este divergenta (deci,
atunci cand sirul
,
in caz contrar, seria este divergenta (deci,
atunci cand sirul ![]() nu are limita sau are limita
nu are limita sau are limita ![]() ).
).
b)
Daca
seria ![]() este convergenta,
atunci seria
este convergenta,
atunci seria ![]() se numeste
absolut convergenta.
se numeste
absolut convergenta.
3.2. Propozitie. Daca seriile ![]() si
si ![]() sunt serii convergente iar
sunt serii convergente iar ![]() ,
atunci seriile
,
atunci seriile
![]() si
si ![]() sunt convergente si avem
sunt convergente si avem
1).![]() 2).
2).![]() .
.
3.3. Propozitie. Daca seria ![]() este convergenta atunci termenul general
este convergenta atunci termenul general ![]() converge
la zero.
converge
la zero.
Reciproc nu este adevarat
Demonstratie. Convergenta seriei este echivalenta cu
convergenta sirului sumelor partiale ![]() .
Deci, exista
.
Deci, exista ![]() ,
,
![]() .
Atunci din
.
Atunci din ![]() ,
prin trecere la limita, deducem ca
,
prin trecere la limita, deducem ca ![]() .
.
Observatie. Afirmatia din propozitia 3.3 reprezinta o conditie necesara de convergenta a unei serii. Daca aceasta conditie nu este verificata atunci seria este divergenta.
De exemplu, seria armonica generalizata
![]() este divergenta deoarece sirul sumelor
partiale
este divergenta deoarece sirul sumelor
partiale ![]() desi, termenul general al seriei
desi, termenul general al seriei ![]() ,
cand
,
cand ![]() .
.
3.4. Propozitie. Daca seria ![]() este convergenta, atunci
seria
este convergenta, atunci
seria ![]() este convergenta
este convergenta
Reciproc
nu este adevarat. De exemplu,
seria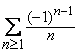 este convergenta, avand suma egala
cu
este convergenta, avand suma egala
cu ![]() ,
in timp ce seria modulului termenilor este seria armonica care este divergenta
(vezi, exemplul 2).
,
in timp ce seria modulului termenilor este seria armonica care este divergenta
(vezi, exemplul 2).
Criterii de convergenta (pentru serii cu termeni reali oarecare)
3.5. Criteriul lui Cauchy Seria
de numere reale ![]() este
convergenta daca si numai daca se verifica conditia
este
convergenta daca si numai daca se verifica conditia
![]() astfel incat
astfel incat 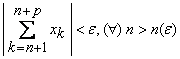 si
si ![]() . (3)
. (3)
Demonstratie. Demonstram implicatia Þ ". Deoarece seria este convergenta, atunci sirul sumelor partiale, ![]() , este un sir de numere reale convergent,
deci este sir Cauchy si avem
, este un sir de numere reale convergent,
deci este sir Cauchy si avem
![]() astfel incat
astfel incat ![]() ,
,
ceea ce este echivalent cu conditia din enuntul teoremei.
Demonstram implicatia inversa ("![]() ").
Conditia din enunt arata ca sirul
").
Conditia din enunt arata ca sirul ![]() este un sir Cauchy de numere reale, deci este
convergent. Asadar, seria numerica este convergenta.
este un sir Cauchy de numere reale, deci este
convergent. Asadar, seria numerica este convergenta.
Exemplu 1. Fie seria ![]() .
Termenul general al sirului sumelor partiale este dat de relatia
.
Termenul general al sirului sumelor partiale este dat de relatia
![]() .
.
Pentru a
stabili natura seriei date, potrivit criteriului lui Cauchy, este suficient sa
aratam ca sirul sumelor partiale este sir Cauchy de numere reale. Fie ![]() ,
oarecare. Atunci pentru orice
,
oarecare. Atunci pentru orice ![]() si
si ![]() suficient de mare putem scrie
suficient de mare putem scrie
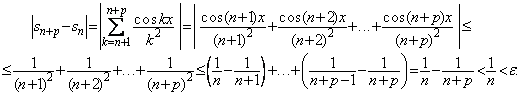
Deci, sirul sumelor partiale este sir Cauchy si In consecinta seria este convergenta.
Exemplu 2. Seria armonica ![]() este divergenta.
este divergenta.
Aratam ca sirul sumelor partiale nu este sir Cauchy. Intr-adevar, avem
![]() ,
, ![]() .
.
Pentru ![]() rezulta ca
rezulta ca ![]() si deci, sirul sumelor partiale
si deci, sirul sumelor partiale ![]() nu este sir Cauchy.
nu este sir Cauchy.
Asadar, seria este divergenta.
3.6. Criteriul lui Abel . Fie seria numerica
![]()
Daca sunt verificate conditiile
![]() este un sir de numere reale pozitive
convergent la zero;
este un sir de numere reale pozitive
convergent la zero;
![]() a.i. pentru
orice
a.i. pentru
orice ![]() sa avem
sa avem 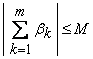 ,
,
![]() (altfel spus, sirul sumelor partiale asociat seriei
(altfel spus, sirul sumelor partiale asociat seriei ![]() este marginit
este marginit
atunci seria ![]() este convergenta
este convergenta
Demonstratie Notam cu ![]() ,
atunci putem scrie
,
atunci putem scrie
![]()
Vom arata ca sirul sumelor partiale asociat seriei ![]() este un sir Cauchy, deci este convergent.
este un sir Cauchy, deci este convergent.
Un calcul simplu ne conduce la urmatoarele evaluari:
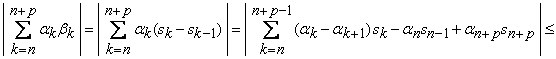
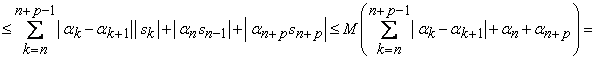
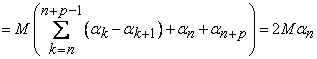 .
.
Deoarece sirul ![]() ,
cand
,
cand ![]() , atunci pentru
, atunci pentru ![]() a.i.
a.i. ![]() avem
avem
![]() .
Asadar, rezulta
.
Asadar, rezulta ![]() si orice
si orice ![]() .
.
Observatie. Acest criteriu nu da conditii necesare de convergenta adica, exista serii convergente care nu verifica conditiile din criteriul lui Abel (vezi, exercitiul 3).
O consecinta directa a criteriului lui Abel este urmatorul criteriu :
3.7. Criteriul lui
Leibniz Daca sirul de numere reale ![]() este
descrescator la zero (
este
descrescator la zero (![]() ,
,
![]() ),
atunci seria
),
atunci seria ![]() este convergenta
este convergenta
Observatie. Criteriul lui Abel este cunoscut sub numele "Criteriul de convergenta Abel-Dirichlet".
3.8. Definitie. Fie
seriile de numere reale ![]() si
si ![]() .
Seria
.
Seria ![]() ,
cu termenul general
,
cu termenul general
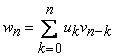
se numeste produsul celor doua serii.
3.9. Propozitie. Daca seriile de numere reale![]() si
si ![]() sunt
absolut convergente, atunci
sunt
absolut convergente, atunci
seria produs 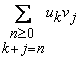 este absolut convergenta
este absolut convergenta
Demonstratie. Deoarece seriile ![]() si
si ![]() sunt absolut convergente, atunci exista
sunt absolut convergente, atunci exista
![]() , a.i.
, a.i. 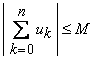 si
si 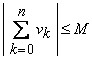 oricare ar fi
oricare ar fi ![]() .
.
Consideram sirul sumelor partiale asociat seriei ![]() ,
unde
,
unde 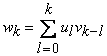 .
Avem
.
Avem
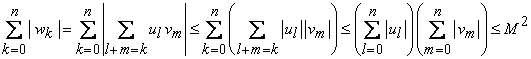
de unde se deduce ca seria produs ![]() este absolut convergenta.
este absolut convergenta.
Exercitiul . Aratati ca urmatoarele serii
i ![]() ii).
ii). ![]()
verifica criteriul lui Abel, deci sunt convergente.
Exercitiul . Aratati ca seria alternanta ![]() verifica criteriul lui Leibniz. Aceasta serie este
convergenta si are suma egala cu
verifica criteriul lui Leibniz. Aceasta serie este
convergenta si are suma egala cu ![]() .
.
Exercitiul . Exista serii convergente care nu verifica criteriul lui Abel-Dirichlet. Astfel in seria,
![]() ,
,
permutand primul termen cu al doilea, al treilea termen cu al patrulea, etc. rezulta seria
![]() .
.
Seria ![]() este convergenta pentru
este convergenta pentru ![]() (din criteriul Leibniz).
(din criteriul Leibniz).
Daca ![]() ,
atunci seria
,
atunci seria ![]() este divergenta si in acest caz spunem ca
seria
este divergenta si in acest caz spunem ca
seria ![]() este semiconvergenta.
este semiconvergenta.
Daca ![]() ,
atunci seria
,
atunci seria ![]() este convergenta si deci seria
este convergenta si deci seria ![]() este
absolut convergenta.
este
absolut convergenta.
Daca ![]() ,
atunci seria
,
atunci seria ![]() este divergenta.
este divergenta.
Vom arata ca seria ![]() este convergenta odata cu seria
este convergenta odata cu seria ![]() si
cele doua serii au aceeasi suma.
si
cele doua serii au aceeasi suma.
Fie ![]() si
si ![]() , sirurile sumelor partiale asociate
celor doua serii. Atunci,
, sirurile sumelor partiale asociate
celor doua serii. Atunci,
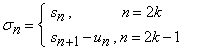 si
si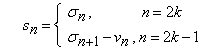 si deci, seriile au aceeasi suma.
si deci, seriile au aceeasi suma.
Seria ![]() este convergenta pentru
este convergenta pentru ![]() ,
totusi, ea nu verifica conditiile criteriului lui Abel-Dirichlet, deoarece
orice alegere am considera pentru sirul
,
totusi, ea nu verifica conditiile criteriului lui Abel-Dirichlet, deoarece
orice alegere am considera pentru sirul ![]() din criteriul mentionat, totusi,
din criteriul mentionat, totusi, ![]() nu este monoton.
nu este monoton.
Exercitiul . Seria ![]() este convergenta intrucat verifica conditiile
criteriului lui Leibniz. Aratati ca suma seriei este egala cu
este convergenta intrucat verifica conditiile
criteriului lui Leibniz. Aratati ca suma seriei este egala cu ![]() .
.
Avem
identitatea: ![]() ,
,
![]() .
.
Sirul sumelor
partiale 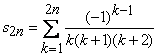 se
poate scrie sub forma
se
poate scrie sub forma
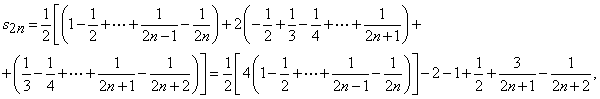
de unde
rezulta ca ![]()
Exercitiul
Aratati ca seria ![]() este convergenta si are suma egala cu
este convergenta si are suma egala cu ![]() .
.
Exercitiul . Fie ![]() .
Seria geometrica
.
Seria geometrica ![]() este convergenta daca si numai daca
este convergenta daca si numai daca ![]() .
In cazul cand
.
In cazul cand ![]() ,
suma seriei este egala cu
,
suma seriei este egala cu ![]() .
.
Solutie. Daca ![]() ,
atunci termenul general al seriei nu converge la zero si deci, seria nu este
convergenta. Daca
,
atunci termenul general al seriei nu converge la zero si deci, seria nu este
convergenta. Daca ![]() ,
atunci
,
atunci ![]() si sirul sumelor partiale are suma
si sirul sumelor partiale are suma 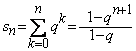 .
.
De aici deducem ca suma seriei este egala cu
![]()
Serii cu termeni pozitivi
3.10. In cele ce urmeaza vom considera numai serii cu termeni pozitivi,
![]() .
.
In acest caz,
daca 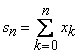 este sirul
sumelor partiale al seriei date, atunci putem scrie
este sirul
sumelor partiale al seriei date, atunci putem scrie
![]() ,
oricare ar fi
,
oricare ar fi ![]() ,
,
de unde rezulta ca sirul ![]() este
crescator. Deducem ca seria
este
crescator. Deducem ca seria ![]() va fi convergenta daca sirul
va fi convergenta daca sirul
sumelor partiale ![]() este marginit, adica,
este marginit, adica, ![]() a.i.
a.i. 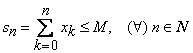
3.11. Criteriul I. Fie ![]() si
si ![]() doua serii cu termeni pozitivi astfel
incat exista
doua serii cu termeni pozitivi astfel
incat exista ![]() cu proprietatea
cu proprietatea ![]() .
.
i) Daca
seria ![]() este convergenta, atunci
este convergenta, atunci ![]() este convergenta
este convergenta
ii) Daca
seria ![]() este
divergenta, atunci seria
este
divergenta, atunci seria ![]() este
divergenta
este
divergenta
Demonstrtie Fie ![]() a.i.
a.i. 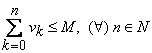 . Din relatiile
. Din relatiile
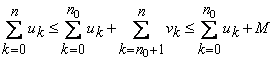 ,
,
rezulta ca sirul sumelor partiale 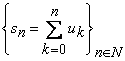 este marginit si deci seria
este marginit si deci seria ![]() este convergenta.
este convergenta.
3.12. Criteriul II. Fie ![]() si
si ![]() doua serii cu termeni pozitivi. Daca
doua serii cu termeni pozitivi. Daca ![]() a.i. sa se verifice conditiile
a.i. sa se verifice conditiile
![]() ,
,
![]()
atunci:
i). daca seria ![]() este convergenta atunci seria
este convergenta atunci seria ![]() este convergenta
este convergenta
ii). daca
seria ![]() este
divergenta atunci seria
este
divergenta atunci seria ![]() este divergenta
este divergenta
Demonstratie Relatia din enunt arata ca pentru orice ![]() ,
,
![]() fixat, avem
fixat, avem
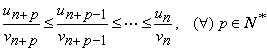
Fie 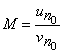 , atunci avem
, atunci avem ![]() pentru
pentru ![]() si
oricare ar fi
si
oricare ar fi ![]() .
Deducem ca
.
Deducem ca ![]() si atunci
si atunci ![]() , de unde rezulta afirmatiile din enunt.
, de unde rezulta afirmatiile din enunt.
3.13. Criteriul III. Fie ![]() si
si ![]() , doua serii cu termeni pozitivi a.i.
, doua serii cu termeni pozitivi a.i. ![]()
i). Daca ![]() ,
atunci cele doua serii au aceeasi natura.
,
atunci cele doua serii au aceeasi natura.
ii). Daca
![]() si seria
si seria
![]() este convergenta, atunci
seria
este convergenta, atunci
seria ![]() este convergenta
este convergenta
iii).Daca
![]() si seria
si seria ![]() este divergenta, atunci
seria
este divergenta, atunci
seria ![]() este divergenta
este divergenta
Demonstratie. Acest criteriu cu limita decurge din criteriul I.
i). Deoarece ![]() si
si ![]() ,
atunci din definitia limitei, pentru
,
atunci din definitia limitei, pentru ![]() suficient de mare, putem scrie
suficient de mare, putem scrie ![]() a.i.
a.i.
![]()
Daca 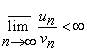 , atunci
, atunci ![]() .
Cum
.
Cum ![]() ,
atunci avem
,
atunci avem ![]() .
.
Deoarece 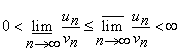 , atunci seriile
, atunci seriile ![]() si
si ![]() au
aceeasi natura.
au
aceeasi natura.
ii). Fie ![]() si
si ![]() a.i.
a.i. ![]() pentru orice
pentru orice ![]() .
Avem
.
Avem ![]() pentru
pentru ![]() .
Cum
.
Cum ![]() convergenta atunci rezulta ca
convergenta atunci rezulta ca ![]() convergenta.
convergenta.
iii). Daca ![]() ,
atunci putem scrie
,
atunci putem scrie ![]() ,
pentru orice
,
pentru orice ![]() ,
fixat si
,
fixat si ![]() .
Cum
.
Cum ![]() divergenta atunci rezulta ca
divergenta atunci rezulta ca ![]() divergenta.
divergenta.
Exemple:
Seria ![]() este divergenta.
este divergenta.
Intr-adevar, definim ![]() si
si ![]() .
Atunci, avem
.
Atunci, avem ![]() . Din criteriul I de comparatie nu putem trage concluzii asupra convergentei
seriei. Cu ajutorul criteriului III, obtinem
. Din criteriul I de comparatie nu putem trage concluzii asupra convergentei
seriei. Cu ajutorul criteriului III, obtinem
![]() ,
deci seriile
,
deci seriile ![]() si
si ![]() au
aceeasi natura, ultima serie fiind divergenta ( !).
au
aceeasi natura, ultima serie fiind divergenta ( !).
Exercitii
(a). Studiati natura urmatoarelor serii :
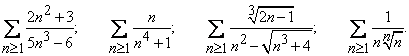 .
.
(b). Determinati suma seriei ![]()
Indicatie. Putem scrie identitatea ![]() unde, prin identificare, gasim
unde, prin identificare, gasim ![]() si
si ![]() .
Atunci termenul general al seriei devine
.
Atunci termenul general al seriei devine
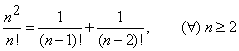
si, prin urmare,
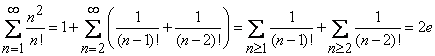 .
.
(c). Studiati natura seriei ![]() .
.
Solutie. Daca ![]() atunci obtinem seria armonica
atunci obtinem seria armonica ![]() .
.
In inegalitatea evidenta
![]() , (2.4)
, (2.4)
daca substituim, succesiv, ![]() obtinem ca subsirul
obtinem ca subsirul ![]() al sirului sumelor partiale
al sirului sumelor partiale![]() ,
este nemarginit superior:
,
este nemarginit superior:
![]()
Asadar, sirul sumelor partiale are limita infinita si deci, seria este divergenta.
Observatie. Inegalitatea (2.4) arata ca sirul sumelor
partiale asociat seriei nu este sir Cauchy. Intr-adevar, daca alegem ![]() ,
deducem
,
deducem
![]() , pentru orice
, pentru orice ![]()
si atunci din criteriul general al lui Cauchy obtinem ca seria este divergenta.
Daca ![]() ,
atunci termenii corespunzatori ai seriei considerate sunt mai mari decat
termenii seriei armonice care este divergenta. Potrivit criteriului I de
comparatie rezulta ca seria
,
atunci termenii corespunzatori ai seriei considerate sunt mai mari decat
termenii seriei armonice care este divergenta. Potrivit criteriului I de
comparatie rezulta ca seria ![]() este divergenta.
este divergenta.
Daca ![]() ,
vom pune
,
vom pune ![]() ,
unde
,
unde ![]() .
Analog inegalitatii (2.4), avem inegalitatea
.
Analog inegalitatii (2.4), avem inegalitatea
![]() , (2.5)
, (2.5)
Procedand ca mai sus, obtinem
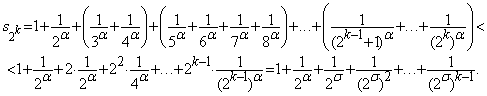
Rezulta ca sumele partiale ale seriei considerate sunt majorate de numarul constant
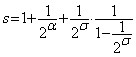
si deci, seria este convergenta.
(ii). Criterii de convergenta (pentru serii cu termeni pozitivi
3.14. Criteriul raportului (criteriul lui d'Alembert[5]).
Fie seria ![]() si
si ![]() respectiv
respectiv
 , atunci
, atunci
i) Daca ![]() ,
atunci seria
,
atunci seria ![]() este
convergenta.
este
convergenta.
ii) Daca ![]() ,
atunci seria
,
atunci seria ![]() este divergenta.
este divergenta.
iii) Daca ![]() ,
atunci seria poate fi oricum ( in acest caz nu putem decide natura
,
atunci seria poate fi oricum ( in acest caz nu putem decide natura
seriei
Demonstratie. Analizam cazul i). Fie ![]() si
si  .
Atunci oricare ar fi
.
Atunci oricare ar fi ![]() ,
exista
,
exista
![]() a.i.
a.i. ![]() .
Daca notam cu
.
Daca notam cu ![]() ,
atunci rezulta
,
atunci rezulta
![]()
Un calcul simplu arata ca ![]() si pentru orice
si pentru orice ![]() .
Deoarece seria
.
Deoarece seria ![]() este convergenta, din criteriul I de
comparatie deducem ca seria data este convergenta.
este convergenta, din criteriul I de
comparatie deducem ca seria data este convergenta.
Observatie. Din inegalitatea ![]() ,
folosind notatia
,
folosind notatia 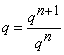 atunci putem scrie inegalitatile
atunci putem scrie inegalitatile 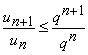 ,
oricare ar fi
,
oricare ar fi ![]() .
Atunci, din criteriul II de comparatie, tinand seama ca seria
.
Atunci, din criteriul II de comparatie, tinand seama ca seria ![]() este convergenta (fiind suma progresiei
geometrice cu ratia
este convergenta (fiind suma progresiei
geometrice cu ratia ![]() ),
rezulta ca seria
),
rezulta ca seria ![]() este convergenta.
este convergenta.
Observatie. Daca ![]() a.i.
a.i. ![]() oricare ar fi
oricare ar fi ![]() ,
atunci si limita superioara
,
atunci si limita superioara 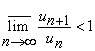 si deci, seria
si deci, seria ![]() este convergenta.
este convergenta.
3.15. Criteriul radacinii lui Cauchy. Fie seria ![]() si
si ![]() ,
atunci
,
atunci
i)
Daca ![]() ,
atunci seria
,
atunci seria ![]() este
convergenta.
este
convergenta.
ii)
Daca ![]() ,
atunci seria
,
atunci seria ![]() este
divergenta.
este
divergenta.
iii)
Daca ![]() ,
atunci cu acest criteriu nu se poate
preciza natura seriei.
,
atunci cu acest criteriu nu se poate
preciza natura seriei.
Demonstratie. Prin
ipoteza ![]() a.i.
a.i. ![]() si deci,
si deci, ![]() ,
de unde rezulta ca seria
,
de unde rezulta ca seria ![]() este
majorata de seria convergenta
este
majorata de seria convergenta ![]() ,
deci este convergenta .
,
deci este convergenta .
3.16. Criteriul lui Raabe si Duhamel. Fie seria ![]() ,
,
![]() si fie
si fie 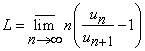
i)
Daca ![]() ,
atunci seria
,
atunci seria ![]() este
convergenta.
este
convergenta.
ii)
Daca ![]() ,
atunci seria
,
atunci seria ![]() este divergenta.
este divergenta.
iii)
Daca ![]() ,
atunci cu acest criteriu de convergenta
nu putem decide natura seriei date.
,
atunci cu acest criteriu de convergenta
nu putem decide natura seriei date.
Demonstratie. i). Fie 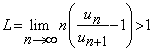 si
si ![]() oarecare, dar fixat. Atunci exista
oarecare, dar fixat. Atunci exista ![]()
a.i. 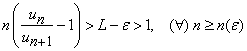 si deci
si deci ![]() .
.
Deducem relatiile
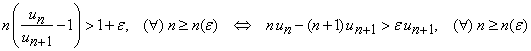
Fie ![]() si
si ![]() .
Atunci, pentru
.
Atunci, pentru ![]() fixat, avem
fixat, avem
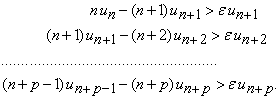
Insumand aceste relatii, dupa reducerea termenilor asemenea, obtinem
![]() .
.
Prin urmare,
pentru orice ![]() si orice numar natural
si orice numar natural ![]() ,
obtinem
,
obtinem
![]() fixat.
fixat.
De aici
deducem ![]() ,
,
![]() fixat, care arata ca seria
fixat, care arata ca seria ![]() este convergenta.
este convergenta.
ii). Daca ![]() ,
fie
,
fie ![]() a.i.
a.i. ![]() .
Exista
.
Exista ![]() a.i.
a.i. 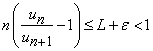 si
deci,
si
deci, ![]() .
.
Ultimele relatii pot fi scrise sub forma echivalenta
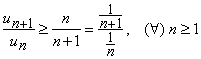
si cum seria ![]() este divergenta, atunci rezulta ca seria
este divergenta, atunci rezulta ca seria ![]() este divergenta.
este divergenta.
Exemplul 1. Fie seria ![]() .
Utilizand unul din criteriile de convergenta studiate, aratati ca seria este
convergenta.
.
Utilizand unul din criteriile de convergenta studiate, aratati ca seria este
convergenta.
Solutie. Notam cu ![]() termenul general al seriei date. Din criteriul
raportului, deducem
termenul general al seriei date. Din criteriul
raportului, deducem
![]()
Prin urmare, cu criteriul raportului, nu putem decide natura seriei. Vom aplica, in continuare, criteriul lui Raabe si Duhamel.
Avem
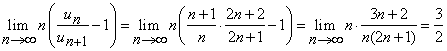
Deci, seria ![]() este convergenta.
este convergenta.
3.17. Criteriul
integral Maclaurin-Cauchy. Fie ![]() ,
o functie continua care ia valori pozitive (
,
o functie continua care ia valori pozitive (![]() ,
,
![]() )
si este monoton descrescatoare pentru
)
si este monoton descrescatoare pentru ![]() ,
,
![]() ,
fixat. Presupunem ca seria numerica
,
fixat. Presupunem ca seria numerica ![]() are termenul general
are termenul general ![]() ,
,
![]() (
unde
(
unde![]() este valoarea functiei
este valoarea functiei ![]() pentru
pentru ![]() ),
deci are forma
),
deci are forma  .
.
Deoarece ![]() este continua pe
este continua pe ![]() ,
atunci
,
atunci ![]() admite primitive pe acest interval. Fie
admite primitive pe acest interval. Fie ![]() o primitiva a functiei
o primitiva a functiei ![]() pe
pe ![]() .
Atunci
.
Atunci ![]() este
derivabila si
este
derivabila si ![]() .
Asadar, functia
.
Asadar, functia ![]() creste
odata cu
creste
odata cu ![]() si deci exista limita
si deci exista limita ![]() ,
finita sau infinita.
,
finita sau infinita.
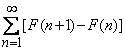 este convergenta. Vom compara aceasta serie cu
seria
este convergenta. Vom compara aceasta serie cu
seria exista ![]() a. i.
a. i. ![]() ,
,
![]() ,
,
![]() , (*)
, (*)
care arata ca
seriile ![]() si
si 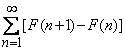 au aceeasi natura, adica, ambele
convergente.
au aceeasi natura, adica, ambele
convergente.
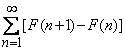 este divergenta si
este divergenta si3.18. Observatie. Criteriul integral MacLaurin-Cauchy se bazeaza pe
compararea seriei numerice cu termenul general ![]() cu integrala
improprie a functiei
cu integrala
improprie a functiei ![]() ,
unde
,
unde ![]() .
.
are limita finita
(sau infinita) cand ![]() ;
vom scrie :
;
vom scrie : ![]() .
.
Demonstratie. Datorita ipotezei putem scrie relatiile
![]() si
respectiv
si
respectiv ![]() .
.
|
Figura 1 |
Fie 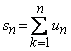 sirul sumelor partiale asociat seriei date.
Atunci
sirul sumelor partiale asociat seriei date.
Atunci ![]() este sir crescator si avem
este sir crescator si avem
![]() , (6)
, (6)
deci, integrala ![]() este convergenta
este convergenta
![]() sirul sumelor partiale
sirul sumelor partiale ![]() este convergent.
este convergent.
Exemplul 1. Fie seria 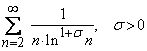 .
Deoarece
.
Deoarece ![]() ,
,
![]() vom alege
vom alege ![]() .
Atunci avem
.
Atunci avem 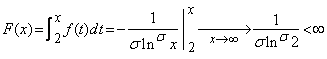 si deci, seria este convergenta.
si deci, seria este convergenta.
Exemplul 2. Fie seria 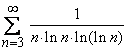 .
Vom alege
.
Vom alege ![]() .
Atunci
.
Atunci ![]() , cand
, cand ![]() .
Asadar, seria este divergenta.
.
Asadar, seria este divergenta.
Exemplul 3. Consideram seria armonica generalizata (seria zeta a lui B.Riemann)
![]()
Alegem ![]() .
Atunci seria
.
Atunci seria ![]() si integrala
si integrala ![]() ,
cand
,
cand ![]() ,
au aceeasi natura. Avem
,
au aceeasi natura. Avem
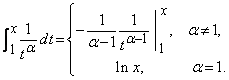
Daca ![]() atunci integrala este convergenta si deci
seria converge catre functia
atunci integrala este convergenta si deci
seria converge catre functia ![]() ,
,
![]() .
.
|
Figura 2. |
Potrivit relatiilor
(2.6) rezulta ca intre integrala si seria ![]() ,
,
![]() putem
scrie relatiile(vezi, fig.2):
putem
scrie relatiile(vezi, fig.2):
![]()
unde ![]() este sirul sumelor partiale al seriei
este sirul sumelor partiale al seriei ![]() .
Asadar, avem
.
Asadar, avem
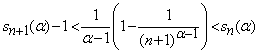 . (7)
. (7)
Din prima inegalitate
(7) deducem inegalitatea ![]() si in consecinta, sunt verificate inegalitatile:
si in consecinta, sunt verificate inegalitatile:
![]() . (8)
. (8)
Daca ![]() ,
din inegalitatea (8), prin trecerea la limita cand
,
din inegalitatea (8), prin trecerea la limita cand ![]() ,
obtinem
,
obtinem
![]() . (9)
. (9)
3.20. Observatie. (i). Pentru ![]() ,
suma seriei armonice
,
suma seriei armonice ![]() ,
care este o serie cu termeni pozitivi, tinde la infinit.
,
care este o serie cu termeni pozitivi, tinde la infinit.
(ii). Seria ![]() este divergenta si
este divergenta si ![]() .
.
(iii). Dubla inegalitate (9) arata ca ![]() .
.
3.21. Observatie. (i). Fie seria ![]() .
.
Daca ![]() ,
atunci seria
,
atunci seria ![]() este absolut convergenta. Daca
este absolut convergenta. Daca ![]() ,
seria este convergenta (din criteriul lui Leibniz, rezulta ca seria
,
seria este convergenta (din criteriul lui Leibniz, rezulta ca seria ![]() este convergenta pentru
este convergenta pentru ![]() )
si avem
)
si avem
![]()
Se verifica usor relatia
![]() .
Atunci
.
Atunci ![]() .
Deoarece
.
Deoarece
![]()
atunci obtinem ca functia ![]() este continua in
este continua in ![]() .
.
(ii). Pentru valori particulare ale parametrului ![]() pot fi cunoscute valorile functiei
pot fi cunoscute valorile functiei ![]() .
De exemplu,
.
De exemplu,
seria ![]() este convergenta si are suma egala cu
este convergenta si are suma egala cu ![]() ;
;
seria ![]() este convergenta si are suma egala cu
este convergenta si are suma egala cu ![]() .
.
3.22. Observatie. (i). Fie seria ![]() .
.
Daca ![]() ,
atunci seria
,
atunci seria ![]() este convergenta. Se verifica usor relatia
este convergenta. Se verifica usor relatia
![]() . (10)
. (10)
Avem
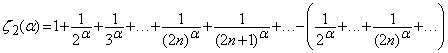 .
.
Atunci,
din (10), obtinem ![]() .
.
(ii). Pentru
valori particulare ale parametrului ![]() pot fi cunoscute valorile functiei
pot fi cunoscute valorile functiei ![]() .
.
De exemplu, seria ![]() este convergenta. Folosind observatia (3.21),
deducem ca suma sa este egala cu
este convergenta. Folosind observatia (3.21),
deducem ca suma sa este egala cu ![]() .
.
Analog obtinem ca seria convergenta ![]() are
suma egala cu
are
suma egala cu ![]() .
.
Calculul aproximativ al unor sume
3.19. Practic, cand nu putem calcula exact suma
unei serii convergente, ![]() ,
atunci putem aproxima suma
,
atunci putem aproxima suma ![]() prin
prin ![]() ,
pentru
,
pentru ![]() suficient de mare. In astfel de aproximari
putem determina valorile lui
suficient de mare. In astfel de aproximari
putem determina valorile lui ![]() astfel ca eroarea absoluta de aproximarea
astfel ca eroarea absoluta de aproximarea ![]() sa fie mai mica decat o anumita valoare
sa fie mai mica decat o anumita valoare ![]() ,
data:
,
data:
![]()
Analizam situatiile:
(a). Fie seria alternanta ![]() ,
unde
,
unde  (din criteriul lui Leibniz seria este
(din criteriul lui Leibniz seria este
convergenta), avand suma partiala
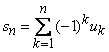
Atunci
![]()
Observam ca sirul ![]() este crescator, iar sirul
este crescator, iar sirul ![]() este descrescator si, cum
este descrescator si, cum
![]()
atunci, putem
scrie ![]() ,
de unde rezulta marginirea acestor siruri. Asadar, avem
,
de unde rezulta marginirea acestor siruri. Asadar, avem ![]() si
si ![]() .
.
Cu ajutorul acestor relatii, obtinem evaluarile
![]()
In consecinta, inlocuind suma ![]() a seriei prin
a seriei prin ![]() ,
facem o eroarea mai mica decat primul termen neglijat, eroarea fiind prin lipsa
daca
,
facem o eroarea mai mica decat primul termen neglijat, eroarea fiind prin lipsa
daca ![]() sau prin adaus daca
sau prin adaus daca ![]() .
Deci, valoarea absoluta a erorii este mai mica decat primul termen neglijat si
vom scrie
.
Deci, valoarea absoluta a erorii este mai mica decat primul termen neglijat si
vom scrie
![]()
De exemplu, daca dorim sa calculam suma seriei
alternate a lui Leibniz, ![]() ,
cu trei zecimale exacte (
,
cu trei zecimale exacte (![]() )
obtinem
)
obtinem ![]() .
.
Deci, insumand primii ![]() termeni ai seriei obtinem
termeni ai seriei obtinem ![]() cu trei zecimale exacte (
cu trei zecimale exacte (![]() 0.693).
0.693).
(b). Fie seria cu termeni pozitivi ![]() .
.
Presupunem ca seria este convergenta si fie ![]() ,
suma seriei. De asemenea, presupunem ca exista
,
suma seriei. De asemenea, presupunem ca exista ![]() a.i.
a.i. ![]() ,
pentru
,
pentru ![]() .
Inlocuind suma
.
Inlocuind suma ![]() a seriei cu suma partiala
a seriei cu suma partiala ![]() putem evalua restul care se obtine sub forma
putem evalua restul care se obtine sub forma
![]()
Asadar, eroarea care se face cand inlocuim suma
seriei cu sirul sumelor partiale ![]() este
este
![]()
De exemplu, daca dorim sa calculam valoarea aproximativa a numarului ![]() cu
trei zecimale exacte, atunci putem sa calculam suma seriei
cu
trei zecimale exacte, atunci putem sa calculam suma seriei ![]() cu trei zecimale exacte. Avem
cu trei zecimale exacte. Avem
![]() , pentru
, pentru ![]()
si deci, ![]() .
Alegem cel mai mic numar natural a.i.
.
Alegem cel mai mic numar natural a.i. ![]() .
Gasim,
.
Gasim, ![]() si deci,
si deci, ![]() .
Asadar
.
Asadar ![]() .
.
Augustin Louis Cauchy (1789-1857), matematician
si mecanician francez, care impreuna cu Gauss a dominat matematica din prima
jumatate a secolului al XIX-lea. A publicat peste 789 de memorii cu subiecte
din matematica, mecanica, astronomie, fizica. A fost unul din fondatorii
analizei matematice; Membru al Academiei Franceze de Stiinte, profesor la
In seria armonica ![]() , fiecare termen
al seriei, incepand cu al doilea, reprezinta media armonica a doi termeni succesivi.
Fie numerele
, fiecare termen
al seriei, incepand cu al doilea, reprezinta media armonica a doi termeni succesivi.
Fie numerele ![]() ; numarul
; numarul ![]() este media armonica a
lui
este media armonica a
lui ![]() si
si ![]() , daca
, daca ![]() .
.
Niels Henrik Abel (1802-1829), matematician norvegian In 1824 stabileste imposibilitatea rezolvarii prin radicali a ecuatiilor generale de gradul cinci Este creatorul teoriei functiilor eliptice
Gottfried Wilhelm Leibniz (1646-1716). matematician si filozof german. Primul presedinte al Academiei de Stiinte din Berlin (la infiintarea careia a contribuit (1700)). Membru in Royal Society din Londra si al Academiei din Paris. Ca matematician a fost autodidact, a inventat calculul diferential (1676). A a studiat lucrarile lui Pascal, Descartes si Huygens. Fondatorul primei reviste stiintifice, Acta Eruditorum (1682). A inventat o masina de calcul.
Jean le Rond d'Alembert (1717-1783), filozof
si matematician francez. Are numeroase cercetarile in mecanica, acustica si
astronomie. In 1743 publica Traité de
dynamique care contine teorema cunoscuta sub numele de Principiul lui d'Alembert: "fortela pierdute ![]() aplicate unui sistem
de puncte materiale supus la legaturi, formeaza un sistem de forte in
echilibru". Acest principiu constitue o metoda de rezolvare a problemelor de
dinamica, numita metoda cinetico-statica. In 1768 a utilizat criteriul de convergenta pentru serii cu termeni
pozitivi, criteriu care ii poarta numele, iar in algebra a enuntat pentru prima
data teorema fundamentala a algebrei.
Propune o metoda de rezolvare a sistemelor de ecuatii diferentiale si studiaza
primul exemplu de ecuatie cu derivate partiale.
aplicate unui sistem
de puncte materiale supus la legaturi, formeaza un sistem de forte in
echilibru". Acest principiu constitue o metoda de rezolvare a problemelor de
dinamica, numita metoda cinetico-statica. In 1768 a utilizat criteriul de convergenta pentru serii cu termeni
pozitivi, criteriu care ii poarta numele, iar in algebra a enuntat pentru prima
data teorema fundamentala a algebrei.
Propune o metoda de rezolvare a sistemelor de ecuatii diferentiale si studiaza
primul exemplu de ecuatie cu derivate partiale.
|