La trigonométrie dans le triangle rectangle est bien utile pour calculer des angles et des longueurs mais hélas, elle se limite aux angles aigus. De plus, les angles que nous avons manipulés jusqu'à maintenant − appelés angles géométriques − ne sont pas orientés ce qui pose un problème pour tous les phénomènes de rotation.
Comment décrire par exemple, le mouvement d'une planète qui tourne sur son orbite ?
Ce genre de questions a conduit les mathématiciens et physiciens à redéfinir et élargir la notion d'angle puis de sinus e 959h74j t de cosinus. C'est ce que nous allons aborder avec ce chapitre !
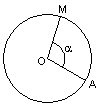 Le cercle ci-contre a pour
rayon 1 : On l'appelle cercle trigonométrique.
Le cercle ci-contre a pour
rayon 1 : On l'appelle cercle trigonométrique.
Complétons le tableau ci-dessous :
|
Mesure de a en degrés | |||||||
|
Longueur de l'arc |
p |
Nous voyons donc que la longueur de l'arc permet de "mesurer" l'angle a
Définition : La mesure d'un angle a en radian est donc la longueur de l'arc qu'il intercepte dans le cercle trigonométrique.
Pourquoi utiliser les radians plutôt que les degrés ?
Car ils permettent de simplifier la plupart des formules et des calculs ou les angles interviennent !
Par exemple, dans le secteur angulaire de rayon R ci-dessous, on a :
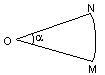 = R a
= R a
Aire = R a
 2) Angles orientés
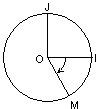
2) Angles orientésDans la figure ci-contre, combien y a-t-il de points M tels que
Pour placer M sans ambiguïté comme ci-contre, nous pouvons orienter cet angle et l'écrire : ( (Ici nous avons tourné dans le sens indirect pour aller de I vers M)
 3) Les différentes mesures d'un
même angle
3) Les différentes mesures d'un
même angleImaginons que l'on enroule une droite graduée comme une ficelle autour du
cercle trigonométrique. Chaque graduation x de la droite va donc correspondre
à un point M du cercle et donc aussi à un angle orienté (
D'après ce qui précède, on peut écrire : ( ) = x radians.
Remarque :
Pourquoi ne pas faire plusieurs tours autour du cercle ?
Correspondant à chaque point du cercle, il y aura alors autant de valeurs de x que de tours!
|
|
Plaçons par exemple les points associés aux réels − On constate que ces trois réels sont associés au même point et sont donc autant de mesures du même angle orienté ( On remarque de plus que On voit donc que si k Z alors 2kp correspond toujours à un nombre entier de tours complets et le nombre − + 2kp sera encore une mesure de l'angle orienté ( |
Bilan :
Tout angle orienté a une infinité de mesures équivalentes : x, x + 2p, x − 2p, x + 4p, x + 2kp
La mesure principale d'un angle est l'unique mesure de cet angle appartenant à ]−p p
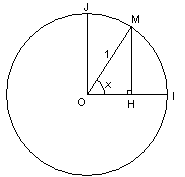 Exprimer les coordonnées du
point M ci-contre en fonction de x :
Exprimer les coordonnées du
point M ci-contre en fonction de x :
xM
yM
Dans le cercle trigonométrique C muni du repère orthonormé (O,
x étant un réel quelconque, on appelle cos x et sin x les coordonnées du point M de C associé à x
Pour tout x de R
< cos x < et −1 < sin x <
cos² x + sin² x = 1
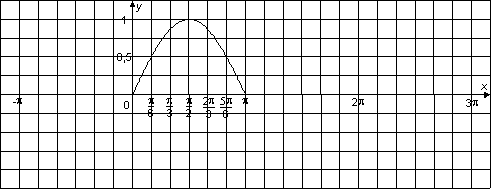
Pour tout x de R, sin (− x) =
En déduire la parité de la fonction sinus
puis, sans calculatrice, compléter ci-dessous sa représentation graphique sur [−p
Pour tout x de R, x et x + 2p sont deux mesures du même angle donc sin (x + 2p
On dit alors que la fonction sinus est périodique de période 2p
Sans calculatrice, en déduire ci-dessous sa représentation graphique sur [p p
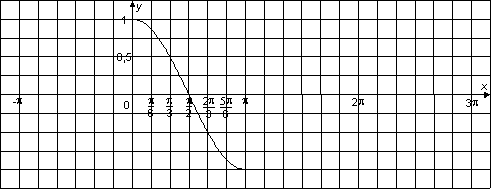
Pour tout x de R, cos (− x) =
En déduire la parité de la fonction cosinus
puis, sans calculatrice, compléter ci-dessous sa représentation graphique sur [−p
Pour tout x de R, x et x + 2p sont deux mesures du même angle donc cos (x + 2p
On dit alors que la fonction cosinus est périodique de période 2p
Sans calculatrice, en déduire ci-dessous sa représentation graphique sur [p p
|