Numerical calculations in C

Numerical calculations in C.

Well, we have a beautiful window with nothing in it. Blank. It would look better if we would draw something in it isn't it? By the way, this is an introduction to C, not to windows.

What can we draw?

Let's draw a galaxy. In his wonderful book "Computers Pattern Chaos and Beauty", Clifford A. Pickover writes:

<<

We will approximate a galaxy viewed from above with logarithmic spirals. They are easily programmable in a computer, representing their stars with just dots. One arm is 180 degrees out of phase with the other. To obtain a picture of a galactic distribution of dots, simply plot dots at (r,q ) according to:

r₁ = e^{[q tan f}

r₂ = e^{[(p q) tan f}

where r1 and r2 correspond to the intertwined spiral arms. The curvature of the galactic arms is controlled by f which should be about 0.2 radians for realistic results. In addition, 0 < q < 1000 radians. For greater realism, a small amount of random jitter may be added to the final points.

>>

He is kind enough to provide us with a formal description of the program in some computer language similar to BASIC. Here it is:

Algorithm: How to produce a galaxy.

Notes: The program produces a double logarithmic spiral. The purpose of the random number generator is to add jitter to the distribution of stars.

Variables:

in = curvature of galactic arm (try in = 2)

maxit = maximum iteration number

scale = radial multiplicative scale factor

cut = radial cutoff

f = final cutoff

Code:

loop1: Do i = 0 to maxit;

theta = float(i)/50;

r = scale*exp(theta*tan(in));

if r > cut then leave loop1;

x = r * cos(theta)+50;

y = r * sin(theta)+50;

call rand(randx);

call rand(randy);

PlotDotAt(x+f*randx,y+f*randy);

end

loop2: Do i = 0 to maxit;

theta = float(i)/50;

theta2 = (float(i)/50)-3.14;

r = scale*exp(theta2*tan(in));

if r > cut then leave loop2;

x = r * cos(theta)+50;

y = r*sin(theta)+50;

call rand(randx);

call rand(randy);

PlotDotAt(x+f*randx,y+f*randy);

end

This are quite clear specs. Much clearer than other "specs" you will find in your future career as programmer. So let's translate this into C. We can start with the following function:

void DrawGalaxy(HDC hDC,double in,int maxit,double scale,double cut, double f)

for (int i = 0; i <= maxit; i++)

We translate both loops into two for statements. The exit from those loops before they are finished is done with the help of a break statement. This avoids the necessity of naming loops when we want to break out from them, what could be quite fastidious in the long term.

I suppose that in the language the author is using, loops go until the variable is equal to the number of iterations. Maybe this should be replaced by a strictly smaller than. but I do not think a point more will do any difference.

Note the cast of i (double)i. Note too that I always write 50.0 instead of 50 to avoid unnecessary conversions from the integer 50 to the floating-point number 50.0. This cast is not necessary at all, and is there just for "documentation" purposes. All integers when used in a double precision expression will be automatically converted to double precision by the compiler, even if there is no cast.

The functions exp and tan are declared in math.h. Note that it is imperative to include math.h when you compile this. If you don't, those functions will be assumed to be external functions that return an int, the default. this will make the compiler generate code to read an integer instead of reading a double, what will result in completely nonsensical results.

A break statement "breaks" the loop.

This statement means

r = (r*cos(theta)) + 5 and NOT

r = r * (cos(theta)+CENTER;

In line 8 we use the rand() function. This function will return a random number between zero and RAND_MAX. The value of RAND_MAX is defined in stdlib.h. If we want to obtain a random number between zero and 1, we just divide the result of rand() by RAND_MAX. Note that the random number generator must be initialized by the program before calling rand() for the first time. We do this in WinMain by calling

srand((unsigned)time(NULL));

This seeds the random number generator with the current time.

We are missing several pieces. First of all, note that CENTER is

#define CENTER 400

because with my screen proportions in my machine this is convenient. Note that this shouldn't be a #define but actually a calculated variable. Windows allows us to query the horizontal and vertical screen dimensions, but. for a simple drawing of a spiral a #define will do.

The function PlotPixelAt looks like this:

void PlotDotAt(HDC hdc,double x,double y,COLORREF rgb)

The first argument is an "HDC", an opaque pointer that points to a "device context", not further described in the windows documentation. We will speak about opaque data structures later. A COLORREF is a triple of red, green, and blue values between zero (black) and 255 (white) that describe the colors of the point. We use a simple schema for debugging purposes: we paint the first arm black (0,0,0) and the second red (255,0,0).

In event oriented programming, the question is "which event will provoke the execution of this code"?

Windows sends the message WM_PAINT to a window when it needs repainting, either because its has been created and it is blank, or it has been resized, or when another window moved and uncovered a portion of the window. We go to out MainWndProc function and add code to handle the message. We add:

.

case WM_PAINT:

dopaint(hwnd);

break;

We handle the paint message in its own function. This avoids an excessive growth of the MainWndProc function. Here it is:

void dopaint(HWND hwnd)

We call the windows API BeginPaint, passing it the address of a PAINTSTRUCT, a structure filled by that function that contains more information about the region that is to be painted, etc. We do not use it the information in it, because for simplicity we will repaint the whole window each time we receive the message, even if we could do better and just repaint the rectangle that windows passes to us in that parameter. Then, we call the code to draw our galaxy, and inform windows that we are done with painting.

Well, this finishes the coding. We need to add the

#include <math.h>

#include <time.h>

at the beginning of the file, since we use functions of the math library and the time() function to seed the srand() function.

We compile and we obtain:

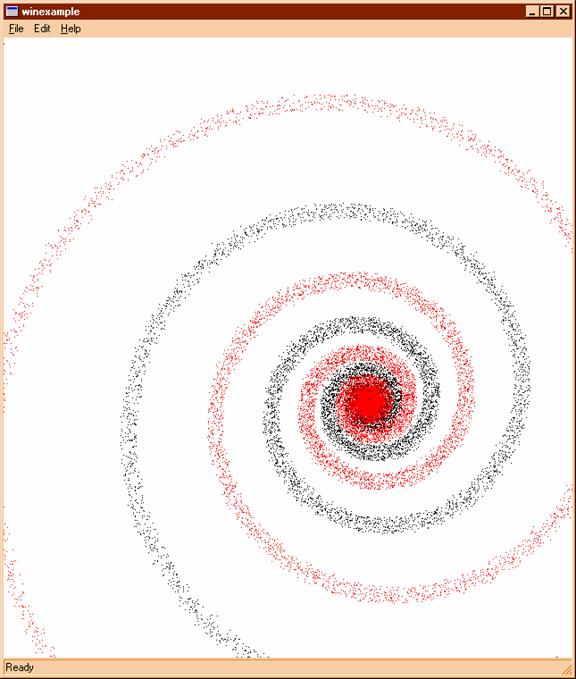
It would look better, if we make a better background, and draw more realistic arms, but for a start this is enough.

There are many functions for drawing under windows of course. Here is a table that provides short descriptions of the most useful ones:

There are many other functions for setting color, working with rectangles, drawing text (TextOut), etc. Explaining all that is not the point here, and you are invited to read the documentation.

Summary:

C converts integer and other numbers to double precision when used in a double precision expression. This will be done too when an argument is passed to a function. When the function expects a double and you pass it an int or even a char, it will be converted to double precision by the compiler.

All functions that return a double result must declare their prototype to the compiler so that the right code will be generated for them. An unprototyped function returning a double will surely result in incorrect results!

Opaque data structures are hidden from client code (code that uses them) by providing just a void pointer to them. This way, the client code is not bound to the internal form of the structure and the designers of the system can modify it without affecting any code that uses them. Most of the windows data structures are used this way: an opaque "HANDLE" is given that discloses none of the internals of the object it is pointing to.