Analiza in curent alternativ a circuitelor

Analiza in curent alternativ a circuitelor

Daca , atunci si

()

Valoarea de varf a fazorului este aceeasi ca si valoarea de varf a formei de unda sinusoidale pe care o reprezinta. Similar cu valoarea efectiva: amplitudinea efectiva a fazorului va fi aceeasi cu amplitudinea efectiva a sinusoidei pe care o reprezinta.

In mod conventional reactantele elementelor L si C sunt valori reale pozitive cu dimensiuni de ohmi, astfel:

X

Y

L

Multiplicarea (inmultirea) logaritmilor prin adunare

Pentru a multiplica numerar avand aceeasi baza se scrie baza si se insumeaza logaritmii lor (exponentii):

. Aceasta obiectie a fost inlaturata prin trecerea la scala decibel (dB).

Belul si decibelul sunt simple modalitati de a exprima rapoarte intre marimi similar. Decibelul este definit ca fiind raportul a doua valori ale puterii electrice.

Ambele marimi ale raportului trebuie sa aibe aceeasi unitate de masura. Astfel, amplificarea amplificatorului din Fig. 1.11 o vom scrie:

Nivele absolute de putere - dBm si dBW

Intrucat scala decibel este foarte utilizata, a intrat in practica curenta utilizarea ei pentru a reprezenta nivelele absolute de putere. Pentru aceasta se utilizeaza ca referinta un nivel standard de putere, adica 1W (dBW) sau 1mW (dBm), conform tabelului de mai jos:

Aceste referinte de putere absoluta se defines ca:

In acest fel, o putere de 10W (10.000mW) se poate exprima ca +10dBW sau +40dBm. O putere de 0.1W se exprima ca -10dBW sau +20dBm. Semnul, in exprimare in dBW sau dBm este foarte important, pentru a evita interpretarile gresite.

1.9. Transferul puterii

Calculul transferului de putere

Dupa cum s-a aratat anterior, debitul instantaneu de putere este dat de relatia:

unde: sunt tensiunea respectiv curentul instantaneu.

Cu toate acestea, acest debit de putere poate reprezenta puterea care este disipata, adesea considerate ca debitul real de putere si puterea care curge sa se inmagazineze intr-o inductanta sau intr-o capacitate, pe care o numim putere imaginara.

Debitul valorii de putere este disipat sau daca se aplica la bornele unei antene, atunci este radiat in spatiu.

Debitul imaginar de putere intr-un circuit de curent alternativ curge inapoi si este stocata in conditiile unui ciclu de incarcare (stocare) cu energia de la varf la zero a unei inductante sau capacitati.

Cand se aplica unei antene, debitul de putere imaginara trece in energia stocata in campul apropiat al antenei.

Practic, suntem interesati mai mult in proiectarea unui sistem de debitul de putere reala. In cazul circuitelor de curent alternativ, puterea reala este data de relatia:

Asfel:

Consideram fazorii tensiune si curent V si I din Fig 1.12.

scaderea unghiurilor , determina diferenta . Fiind partea reala a produsului complex este necesara o multiplicare cu

Atunci:

Aceste expresii si extensiile lor la campurile si vor fi utile pentru exprimarea propagarii puterii in ghidurile de unda si in spatiul liber.

Transferul maxim de putere

In fig. 1.13 de mai jos este prezentata o sursa de tensiune alternativa cu impedanta interna , conectata la o impedanta la sarcina . In general ambele impedante pot fi complexe (au parte reala si parte imaginara).

, adica atunci cand in circuit nici o reactanta nu va reduce amplitudinea curentului I si cu aceasta si reducerea puterii transferate in sarcina.

Puterea de varf, , transformata in sarcina, va fi:

Deci, = amplitudinea de varf a tensiunii.

Prin urmare:

Facand numaratorul egal cu zero, pentru a stabili conditia pentru valoarea maxima a lui (panta zero a lui in raport cu

Nota: Transferul maxim de putere apare atunci cand impedanta de sarcina este egala cu impedanta complexa conjugata a generatorului.

Adica:

Puterea de varf maxima posibila a fi transferata in sarcina este:

In domeniul microundelor, un generator are o impedanta reala, notata cu . In acest caz puterea maxima de varf posibila, devine:

si va fi transferata pe o sarcina

Marimea este denumita tensiune posibila de la generator, deoarece, este tensiunea posibila pe sarcina in conditiile transferului maxim de putere.

Pierderi specifice

Pierderi prin insertie

Am constatat anterior ca transferul maxim de putere intre generator si sarcina apare atunci cand impedantele lor sunt complex conjugate una cu alta.

In practica, doar rareori se cunoaste impedanta echivalenta a sursei de test in domeniul microundelor. Una din masuratorile uzuale este aceea a pierderilor prin insertie, constand in urmatoarea procedura:

Un generator avand impedanta sursei este conectat la o sarcina (Fig. 1.14, a) si puterea transferata pe sarcina va fi notata cu . Apoi, intre generator si sarcina se interpune o retea cu doua porturi (diport) (Fig. 1.14, b), iar puterea transferata pe sarcina o vom nota cu . Pierderile prin insertie (PI) le definim astfel:

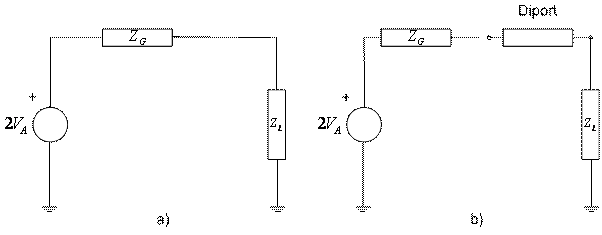
Fig. 1.14

Valoarea PI(pierderi prin insertie) este puternic dependenta de valorile lui si . Fara a cunoaste aceste valori, efectul insertiei diportului nu poate fi prezis cu acuratete. Daca diportul este pasiv (o retea pasiva) pierderile prin insertie pot cuprinde o gama de la 0dB (nu sunt pierderi) pana la o anumita valoare (o valoare pozitiva in dB). Dar nu este necesar sa fie asa. De exemplu, daca sarcina este 25 si impedanta generatorului 50, si daca diportul este un transformator cu pierderi mici, care sa creasca puterea transmisa sarcinii, rezultatul este o valoare de pierderi in dB, negativa sau amplificare in putere si aceasta va fi obtinuta cu un diport pasiv.

Pierderi in traductor

Perspectiva "de amplificare" si lipsa definirii impedantelor sursei si sarcinii in cazul metodei de masura a pierderilor prin insertie, conduce la specificarea unei alte metode de masura, numita pierderi in traductor (PT) definita astfel:

unde, este puterea posibila de la generator.

Daca puterea maxima care poate fi transferata pe sarcina, cu sau fara un diport pasiv, este , pierderile in traductor nu pot fi niciodata mai mici decat unitatea (totdeauna o valoare pozitiva, atunci cand este exprimata in dB). Atunci cand impedantele generatorului si sarcinii sunt complex conjugate una fata de alta, pierderile prin insertie si pierderile in traductor sunt egale. In general, generatorul si sarcina sunt adaptate pe impedanta a cablului de test care le leaga intre ele, satisfacand cerinta de complex conjugat.

In practica industriala, exista obiceiul de a efectua masurarea pierderilor prin insertie. Aceasta se datoreaza usurintei de a efectua masuratori prin substitutie. In primul rand, generatorul si sarcina utilizeaza o conectare speciala pentru a obtine PL1 si apoi substituind diportul se obtine PL2.

Daca generatorul si sarcina sunt adaptate pe o impedanta comuna se obtin aceleasi rezultate ca si prin metoda pierderilor in traductor.

Daca se efectueaza masurarea pierderilor prin insertie cu un analizor de retea, sursa si sarcina sunt in mod uzual rezistive si egale cu a sistemului de teste, respectandu-se cuvintele de la metoda masurarii pierderilor in traductor.

Pierderi determinate de o impedanta serie

Pierderile in traductor determinate de o impedanta serie Z, dispusa intre generatorul adaptat si sarcina, sunt determinate in mod curent de catre circuitele de comutare sau atenuare. (fig. 1.15)

Pierderile in traductor pot fi denumite izolatie atunci cand Z este mare astfel incat sa blocheze cresterea puterii pe sarcina, ca de exemplu in cazul unui intrerupator pus pe pozitia "off"(decuplat). Pierderile in traductor(sau izolatie), ca o functie de Z si se calculeaza astfel:

Inainte de instalarea impedantei Z, in conditiile cand generatorul si sarcina sunt adaptate, tensiunea la sarcina posibila va fi , numita si tensiune de linie, iar curentul prin sarcina, numit si curent de linie, va fi:

Prin introducerea impedantei Z, curentul se micsoreaza. Puterea transferata pe sarcina este proportionala cu patratul curentului prin sarcina:

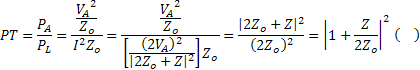
Daca impedanta normalizata, , pierderile pe traductor (izolatie) se va scrie:

Ex.: pentru 5Ω dispusa intre impedanta sursei de 50Ω:

Aceasta poate reprezenta "starea ON" (polarizarea directa) a unei diode PIN, in serie, in linia de transmisie, prevazuta pentru proiectare. Atunci cand diode este trecuta in starea blocata(polarizare inversa) aceasta poate avea o capacitate de exemplu de 0.2pF(starea off). La frecventa de 500MHz, pentru care reactanta diodei este 1590, vom avea izolatia traductorului

Pierderi determinate de o admitanta paralela

Un alt exemplu de pierderi in traductor este acela cand o admitanta este conectata in paralel intre generator si sarcina(fig. 1.16)

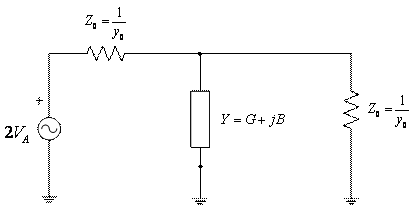
Fig. 1.16

Analogia este similara cu cazul impedantei conectate in serie, obtinandu-se:

unde, admitanta normalizata, y, este: