bare curbe

1. Sa se verifice eforturile unitare care se produc într-o bara curba de sectiune dreptunghiulara, având: b = 3 cm, h = 5 cm, R = 10 cm, solicitata de un moment încovoietor M = 125 kgm. Sa se compare rezultatul cu cel gasit prin aplicarea formulei lui Navier si sa se deseneze ambele diagrame de 18118i822s variatie a eforturilor unitare pe sectiune.

Rezolvare

Aplicând formula lui Navier, se gaseste:

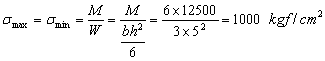
Pentru calculul barei curbe se determina excentricitatea e cu formula:

Se aplica formulele:

A = b x h = 3 x 5 = 15 cm²

d₁ = h/2 - e = 2,5 - 0,208 = 2,292 cm

d₂ = h/2 + e = 2,5 - 0,208 = 2,708 cm

R₁ = R - h/2 = 10 - 2,5 cm

R₂ = R + h/2 = 10 + 2 = 12,5 cm

Reprezentând grafic variatia efortului unitar în figura 1, se obtine linia

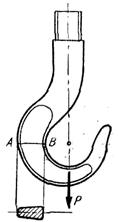dreapta CD prin calculul aproximativ de la barele drepte si hiperbola ENF daca se aplica metoda de calcul exact pentru barele curbe. Eroarea care se comite prin calculul aproximativ este:

Figura 1 Figura 2

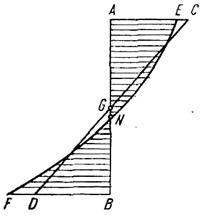
2. Un cârlig de macara are forma din figura 2, sectiunea fiind trapezoidala, cu bazele rotunjite. Forta care solicita cârligul este P = 1000 kgf. Daca dimensiunile sectiunii AB sunt B = 4 cm, b = 2 cm, h = 6 cm, R₁ = 3 cm, se cere sa se calculeze efortul unitar maxim si minim care se naste în sectiune. În sectiunea periculoasa AB, momentul încovoietor are valoarea maxima M = PR, iar forta axiala N = P.

Rezolvare

Raza exterioara este:

R₂ = R₁ + h = 3 + 6 = 9 cm.

Aplicând formula din tabele, se obtine:

Pe de alta parte, pozitia centrului de greutate este:

Excentricitatea axei neutre este:

E = GN = (R₁ + e₂) - r = 3 + 2,666 - 5,153 = 0,513 cm.

Celelalte marimi sunt:

d₁ = r - R₁ = 2,153 cm

d₂ = h - d₁ = 3,847 cm

M = PR = 1000 x 5,666 = 5666 kgcm

R = R₁ + e₂ = 5,666 cm

A = 18 cm².

Se aplica formulele:

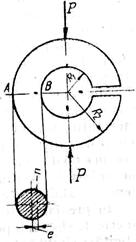
3. Sa se calculeze eforturile unitare care se produc în fibrele extreme ale sectiunii AB a inelului din figura 3, cunoscând ca: R₁ = 40 mm, R₂ = 140 mm, P = 2000 kgf.

Rezolvare

D = R₂ - R₁ = 100 mm

Pozitia axei neutre este:

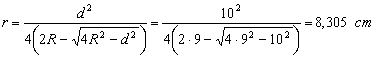
e = R - r = 9 - 8,305 = 0,695 cm.

În sectiunea considerata, eforturile sunt:

M = -PR = - 2000 x 9 = - 18000 kgcm

N = - P = - 2000 kgf.

Având:

A = 78,5 cm² , d₁ = d/2 - e = 4,305 cm , d₂ = d/2 + e = 5,695 cm,

Se afla eforturile unitare: