CALCULUL VALORILOR LIMITA A PARAMETRILOR DE DIAGNOSTICARE

CALCULUL VALORILOR LIMITA A PARAMETRILOR DE DIAGNOSTICARE

Pentru a demonstra metodica de desfasurare a calculului de determinare a valorii limita a parametrilor de diagnosticare, in continuare se va prezenta un exemplu de calcul prin care se urmareste determinarea valorilor limita ale vascozitatii uleiului din motor, la 100 ^oC, folosita ca parametru de d 141j97b iagnosticare. Se stie ca vascozitatea uleiului creste cand filtrele de aer si ulei sunt imbacsite si se reduce cand pompa de benzina permite scapari de benzina in carter sau arderea este incompleta.

Masurandu-se vascozitatea cinematica a uleiului la 58 de vehicule s-a colectat un numar egal de valori ale acestui parametru, care au fost ordonate in ordine crescatoare, ca prim pas de calcul: 4,2;4,6;6,9x2;7,3x2;7,4x3;7,6;7,7x4; 7,8x3; 8x3; 8,2x5; 8,3x3; 8,5x4; 9x2; 9,6; 9,7; 9,8x2; 10,1x4; 10,3x4; 10,6x5; 11x4; 11,3; 12,2; 12,6 (cSt); valoarea nominala a vascozitatii cinematice a uleiului este 8,0 cSt.

Al doilea pas il constituie restrangerea limitelor probelor, retinand probele cu frecventa cea mai mare, care se afla in intervalul 6,9..11,0 cSt si care contin si valoarea nominala. Numarul de valori s-a redus la N* = 53, astfel ca aplicand formula lui Stegers (relatia 1.3) se ajunge la urmatoarea valoare a intervalului histogramei:

ΔS = (11-6,9)/(1+3,3 lg 53) = 0,7

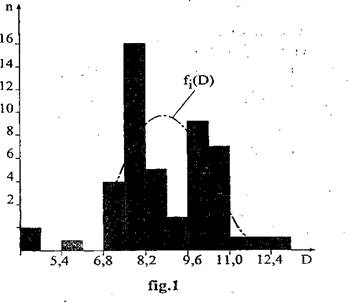
a carei constructie este prezentat in fig. 1.

In acest scop se calculeaza mai intai valorile medii pe interval ale parametrilor de diagno- sticare D_i

D_i = (D_K+1+D_K)/2

luand ca valori de calcul nivelurile vascozitatii de la inceputul intervalului D_K si cea finala D_K+1.

Se inscrie apoi in tabel numarul de probe pe interval, n_i^*, astfel incat

Σn_i^* = N^* = 53.

Se calculeaza densitatea pe interval f_i^*

f_i^* = n_i^*/N^*

produsele D^* = D_i f_i^* si suma lor care reprezinta valoarea medie a parametrului de diagnosticare D_m :

D_m = ΣD^* = Σ D_if_i.

1 - R (D) ,

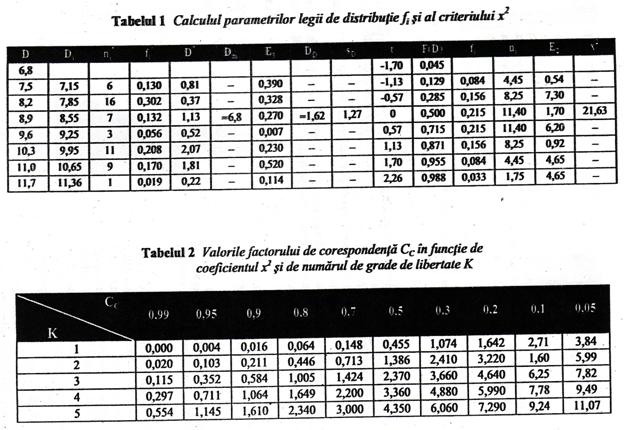
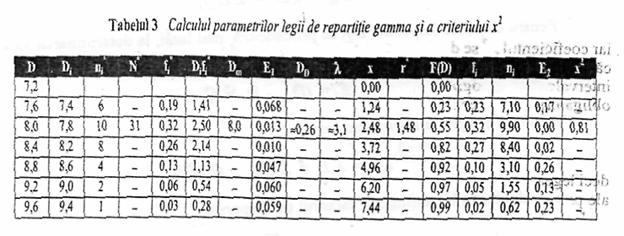
functia de probabilitate R (D) citindu-se in nomograma din fig.3, in functie de x in pśnetele respective, avand ca parametru marimea:

r^* = r-1 = [(D_m - D_o)² / D_D]- 1= λ (D_m - D₀)-1

□ ca si in cazul precedent, densitatea de repartitie se calculeaza prin diferente finite pentru intervalul k :

f_i = F (D_K+1) - F (D_K),

iar coeficientul x² se determina in mod analog. Folosind acelasi tabel 2 si cunoscand ea in cazul legii gamma din numarul de grade de libertate egal cu numarul de intervale ale histogramei (sase) trebuie sa se scada acelasi numar de legaturi obligatorii (trei), rezulta ca factorul de corespondenta are valoarea :

C_C ≥0,8>>0,3 ,

deci legea de repartitie stabilita poate fi folosita pentru determinarea valorilor limita ale parametrului de diagnosticare. .

Urmatorul pas consta in determinarea valorilor limita ale viscozitatii uleiului. in acest caz valoarea limita minima este egala chiar cu parametrul de deplasare:

D_{l min.} = D₀ = 7,2 cSt,

iar cea maxima, care corespunde probabilitatii P > 0.95, se calculeaza fie cu relatiile cunoscute din teoria probabilitatilor, fie, mai putin exact, cu relatia D_l = D_m ± 2√D_D gasindu-se astfel D_max = 9,0 cSt.

Daca se traseaza curba de repartitie integrata (fig.2), se observa ca din totalul masinilor testate 1% vor avea densitatea uleiului sub limita inferioara (adica vor prezenta defectiuni ale sistemului de alimentare), iar 56% vor avea filtrele de aer si ulei imbacsite.