CERCETAREA OPERATIONALA APLICATA IN EXPLOATAREA SI REPARAREA INSTALATIILOR ELECTROMECANICE DE LA BORDUL NAVELOR

CERCETAREA OPERATIONALA APLICATA IN EXPLOATAREA SI REPARAREA INSTALATIILOR ELECTROMECANICE DE LA BORDUL NAVELOR

1. Introducere

Exploatarea si repararea instalatiilor electromecanice navale este o activitate complexa datorita aplicarii celor mai noi realizari ale stiintei si tehnicii, utilizind in acest scop un aparat matematic specific (programe) si mijloace de calcul perfectionate. Avand in vedere cele mentionate, cercetarea operationala ocupa un rol important in realizarea obiectivului propus, respectiv buna functionare a instalatiilor electromecanice. Cercetarea operationala are la baza urmatoarele teorii:

-     444d31e      444d31e teoria deciziei,

-     444d31e      444d31e teoria programarii,

-     444d31e      444d31e teoria grafelor,

-     444d31e      444d31e teo­ria fenomenelor de asteptare,

-     444d31e      444d31e teoria uzurii.

O importanta deosebita in cercetarea operationala il au de asemenea:

-     444d31e      444d31e programarea liniara,

-     444d31e      444d31e programarea neliniara (patratica, hiperbolica),

-     444d31e      444d31e pro­gramarea stochastica,

-     444d31e      444d31e programarea dinamica.

2. Drumul critic in exploatarea si repararea instalatiilor electromecanice de la bordul navei

Drumul critic se reprezinta printr-un grafic retea, care sub forma unei scheme plane arata desfasurarea activi­tatilor si evenimentelor.

2.1. Activitati si evenimente

2.1.1.Activitati.

Pe graficul retea activitatea este reprezentata printr-o sageata orientata in sensul desfasurarii proceselor de intretinere si repa­ratii. O activitate reprezinta o parte distincta dintr-o activitate de exploatare sau reparare, un subproces precis determinat care consuma timp si eventual resurse. Activitatile care necesita timp, insa nu necesita consum de resurse, se numesc asteptari. Activitatile care nu necesita nici timp si nici re­surse si se introduc in graficul retea numai pentru a impune o anumita succesiune tehnologica a activitatilor sau pentru a introduce anumite con­ditii, se numesc activitati fictive si se considera ca au durata zero.

Activitatea care nu este precedata de alte activitati se numeste initiala iar activitatea care nu este urmata de nici o alta activitate se numeste finala.

Durata unei activitati se evalueaza in minute, ore, zile, saptamini, luni etc, in functie de gradul de detaliere a analizei structurii lucrarilor si de nivelul lor de realizare.

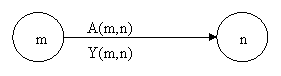In figura 1 se reprezinta o activitate. Prin A(m,n) scris in partea superioara a sagetii se noteaza activitatea, iar prin Y(m,n) scris in partea inferioara a sagetii se noteaza durata activitatii.

Fig.1. Reprezentare activitate

2.1.2.Evenimente.

Extremitatile sagetilor (nodurile retelei) se numesc evenimente si se reprezinta prin cercuri. Evenimentele reprezinta inceperea sau terminarea uneia sau a mai multor activitati. Ele delimiteaza, in functie de retea, ac­tivitatile. La un eveniment pot ajunge sau dintr-un eveniment pot sa plece una sau mai multe activitati, in functie de succesiunea tehnologica a acti­vitatilor.

Evenimentul care se afla la inceputul unei activitati se numeste eveniment precedent activitatii respective iar evenimentul care se afla la finele unei activitati se numeste eveniment urmator al activitatii respec­tive.

Evenimentul care nu are nici o activitate precedenta se numeste eve­niment final.

Fiecare eveniment se numeroteaza cu un numar ce se inscrie in inte­riorul cercului ce marcheaza evenimentul. Numerotarea se face incepandu-se de la evenimentul initial in sensul desfasurarii activitatilor de intre­tinere si reparare.

Reprezentarea grafica

Se utilizeaza urmatoarele metode:

-     444d31e      444d31e metoda graficului retea,

-     444d31e      444d31e me­toda diagramei de succesiune,

-     444d31e      444d31e metoda potentialelor,

-     444d31e      444d31e metoda matriciala.

Se numeste drum intr-un graf, o succesiune in activitati parcursa in sens direct, in care evenimentul final al fiecarei activitati coincide cu eve­nimentul initial al activitatii urmatoare.

2.2.1.Metoda graficului retea

In cadrul acestei metode se au in vedere urmatoarele conditii:

-     444d31e      444d31e activitatile se desfasoara intotdeauna intr-un singur sens, adica nici o activitate nu poate incepe decat dupa terminarea tuturor activitatilor precedente;

-     444d31e      444d31e in cazul in care doua sau mai multe activitati pleaca din acelasi eveniment si desfasurindu-se in paralel ajung la acelasi eveniment se introduc pentru evidentierea lor separata, activitati fictive (vezi fig. 2);

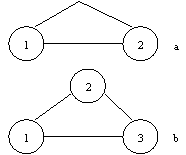
Fig.2.Reprezentarea unei activitati fictive

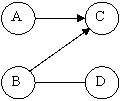
-     444d31e      444d31e in cazul in care inceperea unei activitati de reparatii C depinde de terminarea a doua activitati distincte A si B, in timp ce o alta activitate depinde de una dintre ele (de exemplu activitatea B) atunci interdependenta dintre ele se reprezinta ca in figura 3;

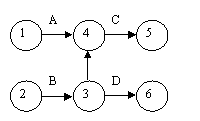
Fig. Interdependenta dintre doua activitati distincte A si B.

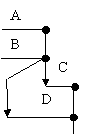
-     444d31e      444d31e cand in cazul repararii unui utilaj, exista activitati care pot fi in­cepute inainte de terminarea completa a unei activitati precedente, atunci, aceasta din urma se poate divide in mai multe parti, fiecare dintre aceste activitati fiind luate in considerare in graficul retea, ca activitati distincte. Aceasta afirmatie se prezinta in figura 4, in care activitatea A (de demontare a unei instalatii pe subansambluri), a fost divizata in patru subactivitati A₁ A₂, A₃, A₄ prin evenimentele si pentru a se putea repre­zenta corect inceperea activitatilor B, C si D;

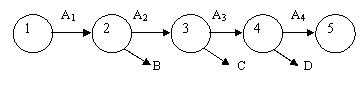
Fig.4. Divizarea unei activitati in mai multe subactivitati

-     444d31e      444d31e un grup de activitati poate fi comasat intr-o singura activitate in cazul cand acest grup porneste de la acelasi eveniment m si se termina cu un singur eveniment n (in figura 5a grupul de activitati B, C, D si F pornesc din evenimentul 2 si se termina in evenimentul 5, iar aceste activitati pot fi comasate intr-o singura activitate H, conform figurii 5b);

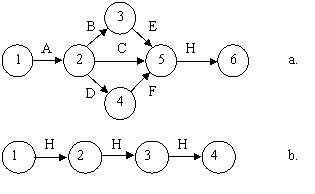
Fig.5. Comasarea unui grup de activitati intr-o singura activitate:

a. - comasarea activitatilor paralele B, E si D, F.

b. – graful echivalent de activitati serie

-     444d31e      444d31e un grup de activitati nu poate fi comasat atunci cind in evenimentele intermediare m si n, pleaca sau sosesc activitati care nu sosesc in eveni­mentul n, sau nu pleaca din evenimentul m ( in figura 6 nu este admisa comasarea activitatilor A, C, E, F si G, intrucat in evenimentul soseste H, care nu pleaca din evenimentul 1);

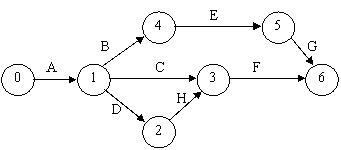
Fig.6. Graf de activitati la care comasarea acestora nu este admisa

-     444d31e      444d31e daca mai multe activitati pornesc dintr-un eveniment initial iar re­prezentarea unora dintre ele este dificila, se poate amplasa evenimentul initial si in alt loc, pe graficul retea, prin simbolizarea lui cu doua cercuri concentrice (fig. 7) avand numerotarea zero (simbolul evenimentu­lui initial);

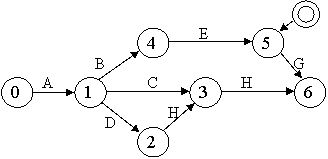
Fig.7.Graf de activitati la care amplasarea evenimentului

initial este in alt loc

-     444d31e      444d31e cand intr-un nod eveniment sosesc si pleaca mai multe activitati, acest nod eveniment indica concomitent terminarea tuturor activitatilor ce converg in nodul eveniment respectiv si inceperea activitatilor ce pleaca din acest nod ( in figura 8, nodul indica terminarea activi­tatilor C si E si inceperea activitatilor G si H);

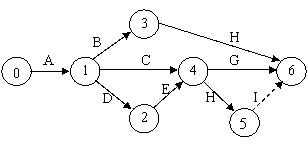
Fig.8. Graf cu noduri evenimente din care sosesc si pleaca

mai multe activitati

-     444d31e      444d31e pentru lucrari complexe se pot intocmi graficele retea partiale (sub-grafuri), care sunt apoi asamblate intr-un grafic retea complet al lucrarii. La asamblarea graficelor partiale trebuie sa se urmareasca ca stadiile de executie din graficele partiale sa corespunda cu stadiile din graficul retea complet. In acest mod, pot fi reprezentate printr-un singur grafic denumit retea sau graf. Graful, asa cum a fost denumit mai sus, este divergent daca pleaca de la un eveniment unic (inceputul unei activitati sau al primelor activitati simultane) si convergent cind are, un eveniment final unic (fi­nele ultimei activitati sau ultimelor activitati simultane), asa cum se poate vedea in figura 9.

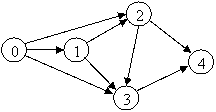
Fig.9. Graf cu activitati divergent-convergente

2.2.2.Metoda diagramei de succesiune

Aceasta constituie o metoda de reprezentare grafica a activitatilor si evenimentelor sub forma unor diagrame de succesiune, in care activitatile sint reprezentate prin segmente orizontale, iar evenimentele prin segmente verticale (fig. 10 a, b, c).

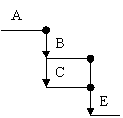
a. b. c.

Fig.10.Diagrame de succesiune

a.A conditioneaza realizarea B si C

b.A si B conditioneaza C si D

c.interconditionarea activitatilor A, B, C si D

2.2.Metoda potentialelor

In acest caz varfurile retelei simbo­lizeaza nu evenimente ci activitati, iar sagetile repre­zinta relatiile dintre activitati.

Fiecarei sageti ii este afectat un numar de unitati de timp care repre­zinta durata minima ce trebuie sa existe intre inceputurile a doua activi­tati legate. Astfel, in figura 11, a activitatea B, nu poate incepe decit dupa opt unitati de timp de la inceputul activitatii A, iar activitatea C, dupa noua unitati de timp din acelasi moment.

Reprezentarea tabelara a graficului din figura 12   Tabelul 1

Ca unitate de masura pentru durata unei activitati se poate adopta: minutul, ora, ziua, saptamina, decada etc.

Durata unei activitati se determina cu relatia:

1.

unde:

Y — este durata activitatii;

Q — cantitatea de lucrari (bucati, ore-norma etc);

n_m — numarul de muncitori din echipa de intretinere si reparatii; N_p — norma de productie;

K — indicele mediu de indeplinire a normei.

Cand activitatile nu pot fi evaluate analitic cu relatia (1), ele se apreciaza pe baza experientei.

Timpul total de realizare a unei lucrari nu poate fi inferior sumei duratelor operatiilor de pe drumul cel mai defavo­rabil.

Avand toate secventele posibile de activitati, incepind cu eve­nimentul initial al unui proces de lucru si terminind cu evenimentul final, una dintre aceste secvente este cea mai mare ca durata. Aceasta secventa (drum) poarta numele de drum critic. Celelalte secvente (drumuri) se numesc drumuri subcritice.