CONTRIBUTII PRIVIND IMBUNATATIREA CONSTRUCTIEI SI CRESTEREA PERFORMANTELOR PLATFORMELOR DE FORAJ MARIN AUTORIDICATOARE ROMANESTI

7.1.ANALIZA METODELOR DE CALCUL ALE PLATFORMELOR DE

Calculul static se aplica platformelor de foraj marin autoridicatoare care au o comportare liniar elastica si comporta doua aspecte: calcul global - pentru determinarea eforturilor din bare, respectiv calculul local - pentru determinarea repartizarii locale a tensiunilor.

 

7.1.2.CALCULUL STATIC

Structurile de rezistenta ale platformelor de foraj marin autoridicatoare pot fi modelate cu elemente de tip grinda dreapta cu rigiditati axiale, de încovoiere, forfecare si torsiune [8], [9] Astfel:

.1.2.2, calculul static global permite determinarea tensiunilor în elementele picioarelor departe de punctele singulare cum sunt îmbinarile tubulare (nodurile). Distributia tensiunilor în zona acestor îmbinari este complicata datorita în special geometriei specifice îmbinarilor tubulare, În vecinatatea cordonului de sudura se înregistreaza, în anumite puncte numite hot-spot, vârfuri de tensiuni care pot fi de pâna la 20 de ori mai mari decât nivelul mediu al tensiunilor din barele secundare ale îmbinarii (spre exemplificare vezi fig.7.2) [17],[148].

Calculul static local are drept scop determinarea distributiei tensiunilor în îmbinarile tubulare cele mai solicitate si aflarea vârfurilor acestor tensiuni.

Acest calcul poate fi efectuat prin trei metode metoda elementului finit; metoda elementului de frontiera; metoda factorilor de concentrare a eforturilor.

Metoda elementului finit porneste de la rezultatele calculului global (eforturile si deplasarile departe de punctele singulare) si foloseste o discretizare fina a îmbinarii tubulare în elemente finite volumice. Detalii asupra acestei metode sunt date în lucrarile [17] si [73]. La ora actuala exista numeroase programe de calculator bazate pe MEF care pot rezolva astfel de probleme.

Fig.7.2

Metoda elementului de frontiera, dezvoltata la Universitatea Southampton din Anglia în anii '70 ai secolului trecut, a fost extinsa la studiul concentrarii tensiunilor din intersectiile carcaselor cilindrice utilizate la tancurile de titei si la determinarea starii de tensiune dintr-o îmbinare de elemente tubulare [7],[17]. Metoda reduce problema tridimensionala la una bidimensionala cu avantaje importante în ceea ce priveste corectitudinea rezultatelor si mai buna reprezentare a conditiilor limita pe domenii infinite.

Metoda factorilor de concentrare a eforturilor (FCE) permite calculul rapid al vârfurilor de tensiune în punctele "hot-spot" prin multiplicarea tensiunilor nominale din bare cu factori de concentrare corespunzatori tipului de efort care le-a generat [17],[114],[120]:

s^E_max= FCE^E s_n^E

unde: FCE^E = factorul de concentrare a efortului, pentru efortul E,

s_n^E = tensiunea nominala din bara, aferenta efortului E.

, (7.7)

unde: [M] = matricea maselor, compusa din:

- masa picioarelor, corpului si instalatiilor sustinute de acesta;

- masa apei aditionale antrenata în miscare de deplasarea structurii;

- masa apendicilor (anozi de sacrificiu, depuneri de scoica si vegetatie pe picioare);

[C] = matricea de amortizare;

[K] = matricea de rigiditate;

= vectorii deplasarilor, vitezelor si acceleratiilor nodurilor structurii într-un sistem de axe fix;

= vectorul fortelor perturbatoare hidrodinamice reduse la nodurile structurii

Vectorul fortelor perturbatoare se poate determina cu relatia Morison [8], [13], [85]:

, (7.8)

în care: = vectorii viteza si acceleratie ale apei în nodurile deplasate ale structurii;

= vectorul vitezelor relative ale apei fata de structura.

Daca deplasarile nodurilor structurii sunt mici se pot aproxima vectorii cu vectorii . Notatiile: r, [C_D], [C_M], [A], [V], au aceeasi semnificatie ca în formula (7.2).

Folosind notatiile:

; ; ,

ecuatia (7.8) devine:

, (7.9)

în care vectorul fortelor perturbatoare va fi functie numai de t si , adica:

(7.10)

Ecuatia matriceala (7.10) este echivalenta cu un sistem algebric de "n" ecuatii cu necunoscutele constituite din deplasarile dinamice pe directiile GLD. Acest sistem poate fi rezolvat prin mai multe metode: metoda integrarii directe, metoda analizei modale, etc. Metoda integrarii directe devine incomoda atunci când n>1000 [25]. Rezolvarea sistemului (7.10) implica doua etape:

1) Aflarea raspunsului liber al structurii, care înseamna rezolvarea ecuatiei matriceale:

(7.11)

Calculul se rezuma la o problema clasica de vectori si valori proprii, în urma caruia rezulta matricea spectrala [W] si matricea modala [f]. Comparând perioada proprie fundamentala a vibratiilor de încovoiere ale structurii cu plaja de valori ale perioadei valurilor se pot obtine informatii asupra riscului aparitiei rezonantei în vibratia structurii datorita actiunii valurilor.

De remarcat ca în ingineria oceanica conditia de rezonanta este inacceptabila.

2) Aflarea raspunsului structurii la actiunea fortelor hidrodinamice se face printr-una din metodele descrise la §7.1.1. Se adopta modelul de val pe baza caruia se calculeaza vectorii . Sistemul (7.10) se integreaza prin metoda adoptata obtinând raspunsul dinamic .

7.1.3.2. Aspecte privind alcatuirea modelului structural

Indiferent de complexitate toate modelele structurale contin aceleasi elemente de baza, adica matricile [M], [C] si [K]. Deci, din punct de vedere matematic, formularea modelului structural înseamna crearea acestor matrice.

Pentru platformele de foraj marin autoridicatoare se pot adopta ca model structural:

modelul dinamic spatial, cu masele concentrate la un numar redus de noduri (fig. 7.3);

modelul dinamic spatial, cu masele concentrate la nodurile structurii reale.

Fig. 7.3

7.1.3.3. Metodele de calcul al raspunsului dinamic

I. Metoda determinista liniara

Se bazeaza pe urmatoarele ipoteze simplificatoare:

valurile marii sunt descrise de modelul liniar Airy [8], [114], [148];

efectul miscarii structurii asupra fortelor hidrodinamice este neglijabil;

componenta de rezistenta a fortelor hidrodinamice poate fi liniarizata.

În aceste ipoteze vectorul din ecuatia (7.7) va fi dat de formula liniarizata a lui Morison [8], [137]:

, (7.12)

în care reprezinta abaterea standard a procesului gaussian v(t) ce descrie câmpul de viteze al particulelor de apa din val [6], [10], [74].

Ecuatia matriceala (7.7), care permite calculul raspunsului dinamic al structurii exprimat în deplasari, devine:

, (7.13)

în care membrul drept este acum cunoscut la orice pas.

Deoarece componentele vectorilor sunt functii armonice de timp de forma:

, (7.14)

Având pulsatia valurilor, iar ecuatiile diferentiale (7.13) sunt liniare, solutia în regimul permanent de miscare va fi tot o functie armonica de timp având aceeasi pulsatie.

Rezolvarea sistemului (7.13) este relativ simpla în acest caz si se poate face prin doua metode:

metoda calculului în complex;

metoda calculului în domeniul de frecventa.

Raspunsul structurii obtinut astfel este unul în deplasari pe directiile gradelor de libertate. Daca se doreste un raspuns în tensiuni într-unul sau mai multe elemente, atunci vectorul se aplica structurii reale si folosind unul din programele de calcul static prin MEF (SAP 90, ALGOR, COSMOS, etc.) se determina variatia în timp a tensiunii din elementul analizat.

Calculul în complex porneste de la rescrierea componentelor excitatiei si raspunsului ca functii complexe de timp. Astfel:

componenta k a excitatiei, va fi scrisa sub forma , unde este amplitudinea complexa, iar este faza acestei forte în raport cu valul;

componenta k a raspunsului, se va scrie , unde este faza acesteia în raport cu valul.

În aceste conditii se poate scrie:

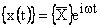; . (7.15)

Înlocuind (7.15) în (7.13) obtinem:

, (7.16)

Din care rezulta vectorul amplitudinilor complexe ale raspunsului:

, (7.17)

În care s-a notat cu [G] paranteza din ecuatia (7.16).

Amplitudinea complexa va fi data de relatia:

, (7.18)

în care: = determinantul matricei [G];

= conjugata complexa a lui;

= determinantul în care coloana k a fost înlocuita cu vectorul .

Daca , atunci , iar pentru orice k = 1...n

Calculul în domeniul de frecventa al raspunsului dinamic al platforme de foraj marin autoridicatoare la actiunea valurilor, considerata ca sistem dinamic liniar în acceptiunea "Teoriei sistemelor" [10] se bazeaza pe utilizarea functiilor de transfer:

, (k = 1, ., n) , (7.19)

unde , în care simbolizeaza transformata Laplace directa.

se obtine din rezolvarea sistemului algebric:

 

 

static) si coeficientii de amplificare dinamica "y" (prin analiza modala);

definirea datelor nodului, care a constat în stabilirea dimensiunilor, a eforturilor si coeficientilor y pentru fiecare nod; s-a tinut cont si de rezultatele masuratorilor de coroziune;

calculul deteriorarilor totale din valuri si vânt, cu programul NODOP (elaborat de autor), în ipoteza platformei noi si folosind expresii FCE si curbe S-N obtinute experimental;

evaluarea deteriorarilor efective medii anuale, cu programul VATEF (elaborat de autor);

stabilirea limitelor duratei de viata inferioara (DVI) si superioara (DVS) ale fiecarui nod;

stabilirea limitelor inferioare si superioare ale duratei de exploatare:

.

Calculul a scos la iveala diferente mari între DVI si DVS pentru nodurile care unesc bare aflate în zonele cu eforturi mari (zona de legatura "corp - picioare" si zona de sprijin pe fundul marii).

Plecând de la aceasta situatie Dima [29] face calculul de oboseala pentru o platforma noua tip "cantilever" pentru care propune noi sectiuni ale barelor în zonele cele mai solicitate, astfel:

în loc de

în loc de

Neajunsurile calculului constau în:

1) Folosirea modelului discret static în care doar un picior este discretizat spatial.

.1.5.4.Analiza calculelor efectuate de Spatoulas Grigorios

Lucrarea elaborata de Spatoulas Grigorios [101] cuprinde:

analiza stabilitatii statice a platformelor de foraj marin autoridicatoare.;

determinarea frecventelor si formelor proprii de oscilatie;

raspunsul dinamic la actiunea valurilor;

analiza dinamica a platformei si turlei aferente.

Analiza stabilitatii statice a constat în evaluarea sarcinii critice de flambaj, prin metoda elementelor finite, folosind programul COSMOS.

Discretizarea structurii s-a concretizat într-un model spatial care respecta structura reala.

Calculele s-au facut pentru doua situatii:

P.F.M.A. la cota minima (z = 69,247 m);

P.F.M.A. la cota maxima (z = 113,423 m).

În ambele situatii calculul a evidentiat ca nu exista pericol de pierdere a stabilitatii.

Determinarea frecventelor si formelor proprii de oscilatie

S-au determinat primele cinci moduri proprii de oscilatie, în cele doua situatii prezentate mai sus.

Datorita dimensiunilor apropriate ale corpului platformei frecventele proprii din primele doua moduri au valori foarte apropiate.

Raspunsul dinamic la actiunea valurilor

S-au facut urmatoarele ipoteze:

directia valurilor este înclinata la 40 fata de axa longitudinala a platformei;

s-au considerat doua tipuri de distributii din valuri:

- prima corespunde unui val activ timp de 4 secunde si timpul dintre doua valuri consecutive este de o secunda;

- a doua corespunde unui val care este activ timp de 4 secunde si timpul dintre doua valuri consecutive este de 5 secunde.

Ambele actiuni au fost considerate periodice, iar înaltimea valului a fost considerata de 5 m.

s-au admis aceleasi doua situatii pentru situatia platformelor de foraj marin autoridicatoare - cota minima z 70 m si maxima z 114 m.

În ambele cazuri s-a obtinut raspunsul dinamic în deplasari pentru punctele de îmbinare dintre picioare si platforma, cu luarea în considerare a primelor trei moduri de vibratie.

Dupa determinarea raspunsului dinamic în deplasari s-a analizat contributia fiecarui mod propriu de oscilatie în configurarea raspunsului dinamic final.

Analiza dinamica a platformei si turlei aferente evidentiaza diferentele care apar atât în frecventele proprii, cât si în raspunsul dinamic.

Neajunsurile calculului constau în:

1) La determinarea raspunsului dinamic la actiunea valurilor s-a considerat doar o directie de actiune a valului.

De asemenea s-a considerat un caz particular de val cu H = 5 m.

Tot în aceasta analiza nu s-a pus problema amortizarilor.

2) Nu s-au avut în vedere fortele date de vânt.

3) Rezultatele calculului dinamic dau deplasari foarte mici în cazul actiunii doar a valului (< 2 mm) ceea ce contravine evidentei si rezultatelor din [75].