![]() MEE2 Cap.2: Convertoare Analog-Numerice
MEE2 Cap.2: Convertoare Analog-Numerice
CONVERTOARE ANALOG-NUMERICE (CAN)
Fie o tensiune
U U ref
U ref
> poate fi reprezentata cu ajutorul unei
serii de puteri de forma:
U
U ref
i
bi
bi
i
înseamna ca U poate fi reprezentat, în principiu, exact, în raport cu Uref prin secventa binara (b b ) de lungime, n general, infinita.
În realitate semnalul trebuie aproximat astfel înc t sa poata fi reprezentat cu un
numar finit de biti.
1 Erori de cuantizare
Sunt doua posibilitati de aproximare:
- trunchiere;
- rotunjire.
Ca urmare a aproximarii respective rezulta o "eroare de cuantizare
Operatia de cuantizare pote fi realizata
cu pas constant cuantizare uniforma) sau
cu pas variabil cuantizare neuniforma)
n echipamentele de masura se foloseste practic în exclusivitate cuantizarea uniforma, de aceea ne vom referi numai la acest caz.
Erori n cazul aproximarii prin trunchiere
Se retin efectiv primii n biti
n
i
n
n i
U t U ref
i
bi DU
i
bi NDU
unde
DU Q n
n
U ref
reprezinta pasul de cuantizare, iar
i
N n i b
i
![]() MEE2 Cap.2: Convertoare Analog-Numerice
MEE2 Cap.2: Convertoare Analog-Numerice
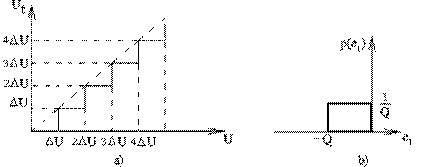
Fig . Eroarea de trunchiere
Eroarea de trunchiere este, evident, o aproximare prin lipsa (fig. 1a).
i
et U t U
U
ref
i b
are valorile extreme:
et max
i
i n
et min
U
ref
i b
U
n 1 U
ref
n
Q
i n
Se vor analiza caracteristicile statistice ale erorii, considerata ca o variabila aleatoare. Se presupune o densitate de probabilitate uniforma a erorii în intervalul -Q, ), (fig. b).
Valoarea medie:
0 Q
E et )
p(et
et det
et
Q
det
Q
Valoarea medie patratica:
e Q 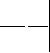
Q
e de t
Q
![]()
Varianta
t t t
Q
12 3 Q
2 2
n
s 2 E e
E e
E e 2 E e
Q Q Q
t t t
t t
12
ref
2 Erori n cazul aproximarii prin rotunjire
Fata de aproximarea prin trunchiere, în acest caz se mai aduna o unitate pe
pozitia cea mai putin semnificativa, daca primul bit neglijat,
valoarea rotunjita se poate exprima prin
bn ar fi fost 1.
![]() MEE2 Cap.2: Convertoare Analog-Numerice
MEE2 Cap.2: Convertoare Analog-Numerice
n i
n
U r U t DUbn 1 U ref
i
bi
bn
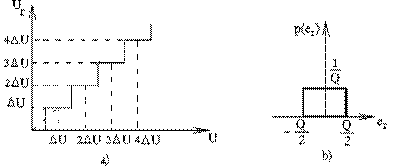
Fig. . Eroarea prin rotunjire
Caracteristica arata ca în figura 2a, în care se observa ca tranzitiile au loc de aceasta data la valorile DU DU 2 n DU
Spre deosebire de aproximarea prin trunchiere, valoarea rotunjita este uneori mai mare, alteori mai mica dec t cea exacta.
Eroarea de rotunjire va fi
b
er U r U
U ref
n
b
U ref
i b
U ref
n
i i
i b
Valorile ei extreme sunt
i n
i n
er max
U ref
n 1 Q
er min
U
ref
i
U
ref
n ) 1 Q
i n
Se va presupune o densitate de probabilitate uniforma n intervalul -Q
Q Rezulta urmatoarele valori medii
Q
E(er ) Q er der
Q
E e 2 )
![]() Q
Q
Q e de
e
r
Q
![]() Q
Q
r
Q
r r Q
Q
r r
![]() MEE2 Cap.2: Convertoare Analog-Numerice
MEE2 Cap.2: Convertoare Analog-Numerice
Observatii.
Eroarea de trunchiere se caracterizeaza printr-o valoare medie negativa, echivalenta cu o componenta continua suprapusa peste semnal, în timp ce eroarea de rotunjire are valoare medie nula.
Dispersiile sunt aceleasi n ambele cazuri.
2 Relatia de conversie
Valoarea trunchiata sau rotunjita se poate exprima n mod exact cu un numar n
de biti.
n cazul trunchierii,
![]()
![]()
N t
i
DU DU
n
n cazul rotunjirii,
N t n
n i b
i
bi
U r U
b N
DU DU
n r
i
n cazul
convertoarelor bipolare, daca limitarea
numarului de
biti este facuta
prin trunchiere si se utilizeaza codul binar deplasat":
1
U U ref n
2 N t
n i b
sau
DU
U
i
n
t
N
n 1 2 n b i b
DU
i
i
Daca limitarea numarului de biti este facuta prin rotunjire,
1
U U ref
2
bn 1
N r
n
i
2 n i b
U
DU
n
r n
i
n i
i
n
![]() N
N
2
b
2
1 b )
2 b b
DU
i
![]() MEE2 Cap.2: Convertoare Analog-Numerice
MEE2 Cap.2: Convertoare Analog-Numerice
Eroarea de cuantizare poate fi echivalata cu un zgomot suprapus peste
semnal este caracterizata de un set de parametrii statistici sunt nsa necesare ipoteze suplimentare referitoare la caracteristicile spectrale ale zgomotului. Vom accepta urmatoarele ipoteze:
zgomotul este alb, având densitatea spectrala de putere N w ) s , constanta n toata banda de frecventa. doua esantioane de zgomot luate
la momente diferite sunt necorelate
- zgomotul este independent fata de semnalul cuantizat.
Ambele ipoteze sunt discutabile. De exemplu:
în cazul unui semnal continuu, eroarea este constanta, deci componenta continua nu are un caracter de zgomot.
în cazul unui semnal aleator modelul este mai apropiat de realitate
t
3 Numar efectiv de biti
Practic, în cazul sistemelor de conversie, în afara zgomotului de cuantizare, datorat CAN, va exista si un zgomot analogic. Acesta provine
pe de o parte din zgomotul suprapus n mod inevitabil peste semnalul
de intrare si
pe de alta parte din zgomotul propriu al amplificatoarelor ce preced conversia.
a
Not nd cu s
varianta acestuia, rezulta ca varianta zgomotului total s 2 este:
s c t
2 s
a
s
Pentru caracterizarea raportului semnal/zgomot total în sistemele de conversie si prelucrare numerica a semnalelor se utilizeaza numarul efectiv de biti, nef. Pentru
a defini aceasta notiune se porneste de la expresia dedusa mai înainte a variantei
zgomotului de cuantizare
s
Q
c
U
![]() ref
ref
2 n
Se presupune ca se aplica la intrare un semnal sinusoidal ce ocupa toata gama convertorului, deci are amplitudinea si valoarea eficace date de :
asa încât
U U
ref
U ef
U ref
![]() 2 2
2 2
![]() MEE2 Cap.2: Convertoare Analog-Numerice
MEE2 Cap.2: Convertoare Analog-Numerice
2
2 U ef U ef
s
![]() c n
c n
2 n
Vom explicita n din relatia de mai sus:
ef n
n
U
, 4
2 U
n log
U ef
log
c
s
s c
4
s
S-a obtinut n acest fel o formula care da numarul de biti necesari pentru un convertor, astfel înc t sa se realizeze un raport semnal/zgomot de cuantizare impus.
nlocuind n relatia de mai sus varianta zgomotului de cuantizare cu varianta
zgomotului total, se obtine marimea numita numar efectiv de biti
U
n log
ef
log
s ![]()
t
![]() Rezulta deci ca numarul efectiv de biti al unui sistem de conversie real se poate defini ca fiind numarul de biti al unui sistem de conversie fara zgomot analogic, caracterizat
prin acelasi raport semnal/zgomot total ca si sistemul real. Relatia de definitie de
mai sus mai poate fi prelucrata n felul urmator
Rezulta deci ca numarul efectiv de biti al unui sistem de conversie real se poate defini ca fiind numarul de biti al unui sistem de conversie fara zgomot analogic, caracterizat
prin acelasi raport semnal/zgomot total ca si sistemul real. Relatia de definitie de
mai sus mai poate fi prelucrata n felul urmator
![]() U
U
2 2 2
ef s c
s a
nef
log 2
![]() s
s
s
log
log
U
s log
c a ef c
U
s
log
ef log
log
a
s
4
s
deci
c c
s
n n log
a
ef
s c
Se obtine astfel o legatura ntre numarul efectiv de biti al sistemului si numarul
de biti al convertorului analog-numeric. Termenul de sub logaritm arata cu c t scade numarul efectiv de biti fata de n, ca urmare a zgomotului analogic.
Evident, nef<n, cu atât mai mult cu cât
s a este mai mare fata de
s c . Ne
propunem sa reprezentam numarul efectiv de biti n functie de raportul zgomot analogic/semnal.
Se pot obtine reprezentari asimptotice utiliz nd urmatoarele aproximari:
c ![]()
MEE2 Cap.2: Convertoare Analog-Numerice
a
Pentrus
a
Pentru s
a
Pentru s
<< s
c
s
c
>> s
nef
nef
n
n log 4 n
![]() s U
s U
![]() s
s
![]() s
s
a ef
a
a
nef
n log 2 log
s
s
log
log
s
log
log
c c
c ef
nu mai depinde de n, astfel nc t marirea numarului de biti ai CAN nu mai conduce la o mbunatatire a numarului efectiv de biti al sistemului.
Graficul reprezent nd numarul efectiv de biti n functie de raportul zgomot analogic / semnal este dat în figura 3. Cu linie îngrosata sunt reprezentate caracteristicile asimptotice deduse mai sus
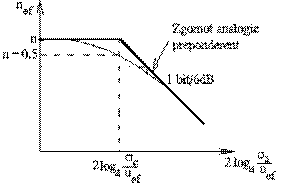
Fig. .Numarul efectiv de biti
Unele instrumente sunt prevazute cu diferite sisteme de prelucrare numerica
mediere, filtrare numerica) ce au drept efect mbunatatirea raportului s z la iesire fata de cel de la intrare. Rezulta ca urmare dupa aceste prelucrari un numar efectiv de biti mai mare decât cel al convertorului analog-numeric de la intrare. Acest câstig poate fi valorificat majorând numarul de biti cu care lucreaza etajele ce urmeaza, inclusiv convertorul numeric-analog de la iesire.
4 Principalele tipuri de convertoare analog numerice
Exista în prezent o mare varietate de scheme de conversie analog-numerica. Alegerea uneia din ele se face pornind de la principalele cerinte impuse în aplicatia concreta viteza, precizie, cost, consum, complexitate . Convertoarele utilizate n instrumentele de masura pot fi clasificate n doua mari categorii:
![]() MEE2 Cap.2: Convertoare Analog-Numerice
MEE2 Cap.2: Convertoare Analog-Numerice
CAN integratoare - lente, precise, ieftine - frecvent folosite n voltmetrele
numerice motiv pentru care vor fi prezentate n capitolul referitor la masurarea tensiunilor si a curentilor.
CAN neintegratoare - rapide, relativ scumpe si de regula mai putin precise dec t primele. Sunt preferate în cazurile în care principala cerinta este viteza, de exemplu n cazul osciloscopului numeric.
5 Convertoare analog-numerice neintegratoare
Pot fi mpartite n doua mari categorii:
cu reactie; - cu aproximari succesive;
- cu rampa n trepte
fara reactie ; - cu rampa liniara;
- paralel;
- serie;
- paralel-serie.
1 Convertoare cu aproximari succesive
Uin
COMP
_
T SC CC
D R A S
![]()
 Q ..Qn W
Q ..Qn W
![]() R M
R M
R E F
b ...bn
Uc C N A
Fig. . Convertorul cu aproximari succesive
RAS - registru de aproximari succesive
COMP - comparator;
CAN - convertor numeric analog
REF - sursa de referinta a CAN;
RM - registru de memorie.
![]() MEE2 Cap.2: Convertoare Analog-Numerice
MEE2 Cap.2: Convertoare Analog-Numerice
Mod de functionare:
Registrul de aproximari succesive este un bloc logic specific acestui tip de convertor. El functioneaza secvential, cu tactul aplicat la intrarea T
Pe intrarea SC start conversie) se aplica semnalul de comanda pentru începerea unui ciclu de conversie, iar D este o intrare de date.
Registrul de aproximari succesive genereaza pe iesirile
N dupa un anumit algoritm
Q Q n
numerele
Dupa primirea semnalului SC , pe frontul primului impuls de tact, se
pune bitul cel mai semnificativ Q 1 si Q i
,
pentru
i
Valoarea corespunzatoare a tensiunii Uc , generata de CAN, este aplicata
comparatorului si comparata cu tensiunea de intrare, Uin
Pe urmatorul tact, semnalul de la iesirea COMP, aplicat pe D, este memorat
n Q , ramânând astfel p na la sfârsitul ciclului de conversie, iar Q
Procesul continua pâna la epuizarea celor n biti. Sfârsitul conversiei este semnalizat prin semnalul conversie completa", CC 1.
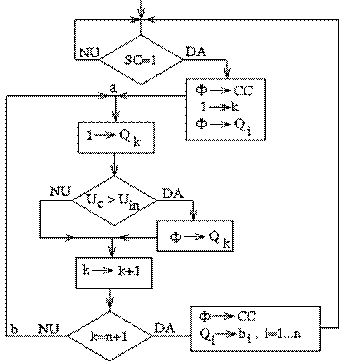
Fig. . Organigrama de functionare a convertorului
Operatiile cuprinse între punctele a si b se executa pe durata unui tact, ta-b =T
(ciclul de tact).
Un ciclu de conversie tCONV va avea minimum n tacte, tCONV = n T. Uneori se prevede un tact n plus pentru nregistrarea rezultatului final si initializari.
![]() MEE2 Cap.2: Convertoare Analog-Numerice
MEE2 Cap.2: Convertoare Analog-Numerice
O schema posibila de RAS: are la baza un registru de deplasare, RD, care
lucreaza pe frontul pozitiv al tactului CLK, deci pe frontul negativ al tactului T.
La fiecare tact, informatia de la iesirea unei celule se transfera n celula urmatoare.

![]()
![]() Fig. . Schema posibila de generare a RAS
Fig. . Schema posibila de generare a RAS
![]() Prima celula are drept intrare DRAS=INIT:
Prima celula are drept intrare DRAS=INIT:
![]() INIT
INIT
Se observa:
QR1 QR 2 QRn 1 S C Q R Q R Q Rn SC
va exista INIT 1 numai dupa golirea completa a registrului RD (Qi
i= n ) si aplicarea comenzii start conversie (SC=1).
daca INIT =0, în n 1 tacte registrul se goleste, oricare ar fi continutul lui initial. Rezulta ca în registru se poate afla în starea 1 cel mult o celula (una din iesiri). Unitatea se va deplasa, n continuare, dintr-o celula n alta, p na când registrul se goleste.
Pentru explicarea functionarii vom porni din momentul c nd INIT
Pe primul tact, secventa ) se aplica CNA rezultatul compararii se traduce prin semnalul COMP va fi memorat n bistabilul D aferent primului bit pe urmatorul front pozitiv starea acestui bistabil nu se va mai schimba pe durata ciclului de coversie
![]() MEE2 Cap.2: Convertoare Analog-Numerice
MEE2 Cap.2: Convertoare Analog-Numerice
Un interval de timp egal cu T, perioada tactului, este disponibil pentru
CNA si COMP. Evident, trebuie deci ca T>tCNA+tCOMP , unde tCNA este timpul de conversie al convertorului numeric-analog, iar tCOMP timpul de stabilire al comparatorului
Când unitatea ajunge n ultima celula (n ) a registrului, se seteaza un bistabil SR care genereaza semnalul CC. Frontul pozitiv al semnalului CC poate fi folosit pentru stocarea datelor într-un registru

Fig. . Functionarea schemei de generare a RAS
Convertorul prezentat este cu comparare nsumare) n tensiune. Privit ca un sistem cu reglare automata, el tinde sa minimizeze tensiunea de eroare aplicata
la intrarea comparatorului, deci sa aduca Uc la o valoare cat mai apropiata de
Uin. Lucrul acesta se poate realiza în limitele erorii de cuantizare.
Deoarece deseori sunt disponibile CNA rapide cu iesire n curent, exista si CAN
cu comparare însumare) n curent (fig. ). Conform ideii expuse mai înainte, sistemul va actiona n sensul de a minimiza tensiunea de eroare, deci
U in RI

Fig. 8. Convertoare cu comparare în curent
![]() MEE2 Cap.2: Convertoare Analog-Numerice
MEE2 Cap.2: Convertoare Analog-Numerice
Precizia acestui tip de convertor este determinata de
calitatea CNA,
precizia tensiunii de referinta, URef
calitatea comparatorului.
Timpul de conversie este dat de tCONV
n T
Frecventa de tact maxima este determinata de viteza CNA si a comparatorului.
Prin structura sa este adecvat realizarii sub forma integrata. Exista RAS-uri integrate, de exemplu AM 3 8 biti), AM 4 0 biti), dupa cum exista si convertoare complete ntr o capsula. n forma integrata, monolitica sau hibrida,
se realizeaza CAN de - 4 biti cu timpi de conversie cuprinsi de regula în domeniul ms
Exemple de asemenea convertoare produse de firma Analog Devices:
AD - convertor de 2 biti si timp de conversie ms
AD - convertor de 8 biti si timp de conversie
ms . O
particularitate a acestui circuit este faptul ca nu necesita semnal de tact. Acesta este realizat din semnalul de start conversie, trecut printr-
o linie de ntârziere, realizata cu porti logice, având atâtea sectiuni, câte impulsuri de tact sunt necesare pentru o conversie completa.
2 Convertoare cu rampa în trepte
Un convertor mai ieftin nlocuind registrul de aproximari succesive cu un bloc logic de control, (BLC) mult mai simplu (figura
Mod de functiobnare:
odata cu aplicarea comenzii start conversie' (SC), bistabilul SR trece în starea 1 si deschide poarta P ce permite accesul impulsurilor de tact catre numarator.
numaratorul ncepe sa numere pornind din starea , iar numarul respectiv este aplicat pe intrarile convertorului numeric-analog.
la iesirea conv. Numeric analog va rezulta deci o tensiune de forma unei rampe n trepte.
procesul continua pâna când tensiunea Uc depaseste nivelul Uin
in momentul c nd acest nivel a fost depasit, comparatorul trece în starea 1
si reseteaza bistabilul. se blocheaza poarta P si se opreste accesul impulsurilor de tact catre numarator. Totodata se semnaleaza sf rsitul
![]() MEE2 Cap.2: Convertoare Analog-Numerice
MEE2 Cap.2: Convertoare Analog-Numerice
![]() conversiei prin
semnalul
CC si
se transfera continutul numaratorului n
conversiei prin
semnalul
CC si
se transfera continutul numaratorului n
registrul de memorie RM (figura 10).
 CC S T
CC S T
S Se
R Q
COMP
CLK
CLR
N U M
Uin
Q ..Qn W
![]()
![]() R M
R M
R E F
b ...bn
Uc C N A
Fig. . Convertor cu rampa n trepte
Uc
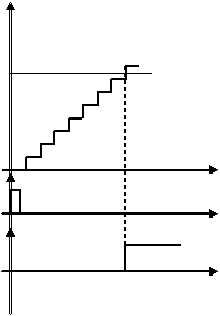 Uin
Uin
SC CC
Fig.10. Functionarea convertorului cu rampa n trepte
Timpul de conversie este dependent de tensiunea Uin, conform relatiei
tCONV
U in T
DU
![]() MEE2 Cap.2: Convertoare Analog-Numerice
MEE2 Cap.2: Convertoare Analog-Numerice
Valoarea maxima este de nT , deci creste exponential cu numarul de biti. Cum alegerea perioadei tactului T este supusa acelorasi restrictii ca în cazul convertorului cu aproximari succesive, rezulta ca în general, acest convertor este mai lent, mai simplu, deci mai ieftin si comparabil ca precizie cu convertorul cu aproximatii succesive.
3 CAN cu rampa liniara convertor tensiune-timp)
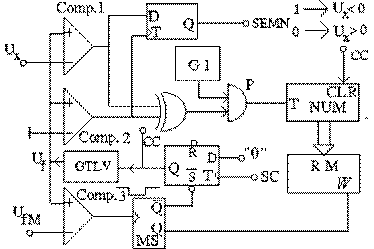
Fig. . CAN cu rampa liniara
Mod de functionare:
GTLV este un generator de tensiune liniar variabila comandat genereaza
o rampa liniara crescatoare ncep nd de la nivelul UfM, pe durata c t tensiunea de comanda are nivel logic 0.
Bucla formata de COMP3, MS si bistabilul D are rolul de a permite pornirea acestei tensiuni atunci când se aplica un front pozitiv pe intrarea SC, si oprirea, când s-a atins nivelul UfM
Panta TLV este m=UfM T
În figurile 12a si b sunt date formele de unda în cazurile U x <
si respectiv
![]() U x > . Din analiza acestora rezulta urmatoarele
concluzii:
U x > . Din analiza acestora rezulta urmatoarele
concluzii:
durata deschiderii portii P este n ambele cazuri data de
t p t
t
x ![]()
![]()
m 1 U
T U x
U
fM
deci circuitul efectueaza o conversie tensiune-timp
![]() MEE2 Cap.2: Convertoare Analog-Numerice
MEE2 Cap.2: Convertoare Analog-Numerice
- iesirea bistabilului D din partea superioara a schemei va avea nivel logic 0
daca tensiunea convertita este negativa si 1 daca aceasta este pozitiva, deci
ea indica semnul tensiunii
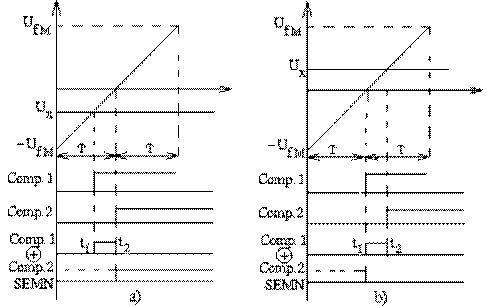
Fig . Formele de unda în cazurile U x <
si respectiv U x
>
n continuare problema se reduce la masurarea numerica a unui interval de timp
Numaratorul NUM numara impulsurile date de un generator de tact GI pe durata cât poarta P este deschisa.
Daca frecventa tactului este fr Tr, numarul de impulsuri contorizate de numarator pe durata deschiderii portii, tp este
![]() t p T
t p T
N x
Tr Tr
U x
U fM
La cap de scara
U CS
U fM pentru un convertor lucr nd cu n biti,
inclusiv bitul de semn
n
N xCS
Tr
Rezulta deci un timp de conversie tconv T n )Tr Frecventa tactului poate
fi mai mare decât în cazul convertoarelor cu reactie prezentate mai înainte, fiind limitata n principal de viteza de lucru a numaratorului. De exemplu, pentru
biti si fr MHz,
Tr ms rezulta
tconv
ms ms ceea ce
corespunde unui convertor cu performante medii în ceea ce priveste viteza.
![]() MEE2 Cap.2: Convertoare Analog-Numerice
MEE2 Cap.2: Convertoare Analog-Numerice
Rezolutia
deci este
DU x se obtine din
T DU x
Tr U fM
O rezolutia buna implica:
DU x
U fM
Tr
T
o frecventa de tact fr mare si
panta UfM T mica.
Precizia este determinata de:
liniaritatea tensiunii liniar variabile si precizia pantei acesteia;
precizia si stabilitatea frecventei fr
calitatea comparatoarelor COMP1,2.
4 CAN paralel
Convertoarele paralel sunt, din punct de vedere al conceptiei, cele mai simple si sunt totodata cele mai rapide. În figura 13 este prezentata schema unui asemenea convertor de trei biti.

Fig. . CAN paralel pe trei biti
Cu ajutorul divizorului format din cele 8 rezistoare se realizeaza tensiunile de prag pentru cele 7 comparatoare. Acestea sunt: Uref
Uref Uref. Se mai poate eventual utiliza un al optulea comparator,
av nd drept prag tensiunea / 1 U ref , cu scopul sesizarii depasirii.
![]() MEE2 Cap.2: Convertoare Analog-Numerice
MEE2 Cap.2: Convertoare Analog-Numerice
Semnalele de la iesirile comparatoarelor indica nivelul tensiunii n asa-numitul
"cod termometric", ineficient din punct de vedere al numarului de biti utilizati.
În consecinta va fi necesara o logica de decodare, care realizeaza trecerea la trei biti.
Precizia convertorului este determinata de calitatea comparatoarelor si de
precizia cu care sunt realizate pragurile. Aceasta din urma, este, la r ndul ei dependenta de precizia realizarii divizorului rezistiv
Dezavantajul major al schemei consta n numarul mare n 1), de
comparatoare de mare viteza . Aceasta implica si consumuri foarte mari.
Utilizând aceasta tehnica, se realizeaza n prezent convertoare de cel mult 6-8 biti, de viteza mare timpi de conversie de zeci de nanosecunde) utilizate pentru achizitia semnalului n osciloscoapele numerice, sistemele video, instalatii radar.
Ca exemplu, circuitul AD90 , produs de Analog Devices, este un convertor de
8 biti, cu o rata de conversie maxima de 0 Mesantioane/secunda.
5 CAN paralel-serie
Având n vedere complexitatea ridicata a convertoarelor paralel în cazul în care este necesar un numar mai mare de biti, se pot realiza combinatii de asemenea convertoare, fiecare lucrând pe maximum 4-5 biti.
O asemenea schema este data în figura 14, unde se realizeaza un convertor de
biti utiliz nd doua convertoare paralel de 4 biti. Primul CAN genereaza primii
biti cei mai semnificativi) ai rezultatului.

Fig . Realizarea unui convertor de 8 biti cu 2 convertoare paralel cu 4 biti
Valoarea cuantizata pe 4 biti este apoi aplicata unui CNA, si rezultatul este scazut din semnalul initial, evaluându-se în acest mod eroarea de cuantizare.
La efectuarea acestei scaderi, semnalul de intrare va trebui sa fie ntârziat cu un
timp egal cu timpul de conversie al primului CAN. Eventual, se poate renunta la
![]() MEE2 Cap.2: Convertoare Analog-Numerice
MEE2 Cap.2: Convertoare Analog-Numerice
aceasta ntârziere, daca se utilizeaza un circuit de esantionare-memorare la
intrare, care sa mentina semnalul aplicat la intrarea convertorului constant pe durata unei conversii.
n continuare, eroarea rezultata dupa prima conversie este si ea cuantizata n al
doilea convertor, care genereaza ultimii 4 biti ai rezultatului. n acest mod se obtine un convertor de 8 biti utiliz nd 0 de comparatoare, n loc de , c te ar
fi fost necesare în varianta paralel. Evident, si timpul de conversie va fi mai mare, el incluz nd de doua ori timpul necesar unui CAN, plus timpul de conversie al CNA
Un exemplu de asemenea convertoare este familia AD7820, 7821, convertoare
de 8 biti n doua etape, lucr nd la circa 1MHz. Un convertor mai rapid este
AD , lucr nd cu 9 biti, la o frecventa maxima de 30MHz
2 5 6 Convertoare de tip pipe-line
n general timpul de conversie al unui convertor analog numeric este definit ca intervalul de timp scurs din momentul esantionarii semnalului analogic pâna la generarea codului numeric corespunzator N.
n multe aplicatii ne intereseaza mai mult perioada cu care poate fi esantionat
semnalul, decât întârzierea cu care este generata iesirea. În schemele prezentate p na acum, cei doi timpi erau practic identici se poate prelua un nou semnal numai dupa ce s-a terminat prelucrarea semnalului precedent).
O categorie de convertoare de mare viteza utilizeaza principiul pipe-line"
bazat pe mai multe convertoare, prelucr nd simultan esantioane succesive ale semnalului. Pe aceasta cale se obtin convertoare cu o perioada de esantionare de câteva ori mai mica dec t timpul propriu-zis de realizare a unei conversii. Altfel spus, convertorul introduce o ntârziere mai mare dec t perioada de esantionare.
La limita, acestea pot fi convertoare de 1 bit (comparatoare), conform schemei
din fig.
Schema acestui convertor de n biti functioneaza în n tacte.
Cele n sectiuni ale convertorului sunt separate prin circuite de esantionare/ memorare (E/M). Acestea esantioneaza simultan semnalele prezente la intrarile lor
Primul CAN compara semnalul de intrare cu
U ref
![]() MEE2 Cap.2: Convertoare Analog-Numerice
MEE2 Cap.2: Convertoare Analog-Numerice
CNA care urmeaza preia bitul dat de CAN si genereaza, la rândul lui o
tensiune egala cu 0 sau cu
sau
U ref , dupa cum bitul de intrare are valoarea 0
Aceasta valoare se scade din semnal, iar reziduul" astfel obtinut se aplica
etajului urmator, care îl compara cu
U ref , si asa mai departe.
Ca urmare, la primul tact, n prima celula se obtine primul bit; la tactul al doilea se obtine în celula a doua bitul al doilea, iar în prima celula MSB al urmatorului esantion, si asa mai departe.

Fig. 15. CAN realizat cu comparatoare
Perioada tactului, determinata de timpul de conversie al unei celule, poate avea valori reduse.
Perioada de esantionare este data de acest tact, dar rezultatul referitor la o conversie se obtine la iesirea logicii de reordonare dupa n tacte
Configuratia de mai sus corespunde unui convertor de tip serie.
În figura 16 este data o schema în care se utilizeaza mai multe sectiuni de 4 biti
(configuratie paralel-serie).
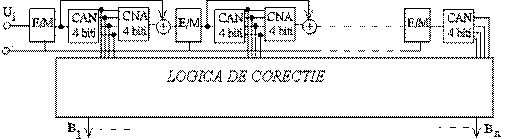
Fig. . CAN paralel serie
![]() MEE2 Cap.2: Convertoare Analog-Numerice
MEE2 Cap.2: Convertoare Analog-Numerice
Numarul total de biti obtinuti nu este totusi egal cu numarul de sectiuni
înmultit cu 4. Aceasta deoarece la fiecare din treptele ce urmeaza dupa
prima este necesara o operatie de corectie care consuma un bit.
Astfel, daca n schema din figura 6 se utilizeaza 3 sectiuni, numarul de biti obtinuti va fi +
Necesitatea operatiei de corectie rezulta
n primul r nd din faptul ca fiecare din sectiuni lucreaza cu aproximare prin trunchiere, asa încât reziduul sa fie n permanenta pozitiv, iar convertorul, n ansamblu, lucreaza cu aproximatie prin rotunjire.
în al doilea rând, fiecare din convertoarele paralel de 4 biti poate fi afectat de o eroare de nelinearitate, ce poate eventual depasi pasul de cuantizare. Eroarea respectiva poate fi corectata prin adaugarea bitului suplimentar.
Pentru a ilustra aceasta idee, sa consideram un convertor cu doua sectiuni, prima
de 4 biti, a doua de 5 biti. La iesirea primului CAN se obtine valoarea trunchiata
la 4 biti incluz nd nsa si o anumita eroare de neliniaritate. Not nd cu U valoarea exacta a semnalului de intrare, semnalul la iesirea primului CAN corespunde valorii
U t enl U et enl
unde
et <
reprezinta eroarea de trunchiere la 4 biti, iar
enl este eroarea de
neliniaritate a primului convertor. Dupa CAN, care are o precizie corespunzatoare unui convertor de 8 biti, se obtine prin scadere
U U et enl et enl
Dupa a doua conversie se obtine
et enl e
unde e ) reprezinta eroarea totala a convertorului al doilea. Prin adunarea celor doua rezultate se obtine
U et enl et enl e U e
Este posibil ca
et enl sa depaseasca nivelul
DU al primului convertor de
biti. De aceea, este necesar un bit suplimentar la a doua conversie, pentru a putea corecta eroarea primei conversii.
![]() MEE2 Cap.2: Convertoare Analog-Numerice
MEE2 Cap.2: Convertoare Analog-Numerice
Ca exemplu se poate da familia de convertoare AD , , , realizate
de Analog Devices. Acestea realizeaza o conversie de 2 biti utilizând trei sectiuni de 5 si 5 biti, la frecvente de esantionare maxime de - 0 MHz.
Combinatie de mai multe CAN lucr nd n paralel, decalat n timp
Exista cazuri c nd nici viteza realizata de un convertor paralel nu mai este suficienta. In asemenea cazuri pot fi utilizate combinatii de convertoare paralel lucr nd n paralel, dar cu intrarile decalate în timp. Un exemplu este reprezentat
de convertorul ultrarapid din osciloscopul numeric HP54 1 (Hewlett-Packard care realizeaza o frecventa de esantionare de1 GHz, deci un timp de conversie
de 1 ns figura

Fig . Convertorul din osciloscopul numeric HP
Se utilizeaza 4 convertoare foarte rapide paralel, cu o constructie mai speciala cu
![]() un timp
de conversie
de circa
TCONVi= 4 ns. Ele sunt precedate
de circuite
de esantionare memorare,
comandate
pe r nd
prin semnalele S
H i Acestea
esantioneaza semnalul pe durata cât se aplica pe intrarea de comanda nivel logic
un timp
de conversie
de circa
TCONVi= 4 ns. Ele sunt precedate
de circuite
de esantionare memorare,
comandate
pe r nd
prin semnalele S
H i Acestea
esantioneaza semnalul pe durata cât se aplica pe intrarea de comanda nivel logic
" si mentin la iesire valoarea memorata a semnalului pe durata c t semnalul de comanda este pe nivel ". Pentru a se realiza viteza necesara sunt realizate în tehnologia GaAs
Timpul de esantionare (starea S) s-a presupus inclus n TCONVi. În aceasta
situatie TCONV 5 TCONV i
![]() Cele 4 semnale S
H i cu perioada T sunt formate pornind de
la un tact de perioada
T si sunt decalate n timp, ca n figura
Cele 4 semnale S
H i cu perioada T sunt formate pornind de
la un tact de perioada
T si sunt decalate n timp, ca n figura
![]() MEE2 Cap.2: Convertoare Analog-Numerice
MEE2 Cap.2: Convertoare Analog-Numerice
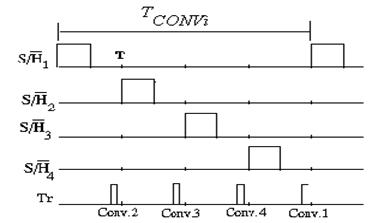
![]() Fig. 18. Realizarea
celor 4 semnale S H i
Fig. 18. Realizarea
celor 4 semnale S H i
Rezultatele obtinute la iesirile celor 4 convertoare sunt selectate pe r nd de
un multiplexor, ale carui semnale de selectie sunt comutate cu perioada T si retinute ntr un registru de stocare.
![]() Între semnalele S
H i si tactul din care sunt
formate acestea
vor
exista
niste mici întârzieri datorate timpilor de propagare. În plus, aceste întârzieri pot sa nu fie riguros egale.
Între semnalele S
H i si tactul din care sunt
formate acestea
vor
exista
niste mici întârzieri datorate timpilor de propagare. În plus, aceste întârzieri pot sa nu fie riguros egale.
Aceste variatii ale momentelor de esantionare pot provoca erori mari în amplitudine n cazul unor semnale cu viteza de variatie foarte mare (de frecventa mare). Pentru a evita aceasta sursa de erori se utilizeaza un circuit S/H comun, de foarte mare viteza, la intrare, comandat de un singur tact
(acela de perioada T). S Hi esantioneaza semnale retinute la momentele corecte de S/H, astfel încât eventualele decalaje în timp ale semnalelor S Hi
nu mai conteaza.
Varianta de achizitie bazata pe memorare analogica
O varianta ieftina si de o viteza relativ ridicata 0 Mesant/s) combina memorarea analogica la viteza mare, utilizând o memorie CCD (cu transfer de sarcina), urmata, de o conversie relativ lenta (convertor cu aproximari succesive) Vom avea în vedere, ca exemplu, sistemul de achizitie al osciloscopului
(Tektronix
ntr-un dispozitiv CCD semnalul este memorat prin intermediul sarcinii electrice
ce poate fi transferata de la intrare în celulele respective. Citirea se face prin transferul spre exterior a acestei sarcini. În cazul de fata se utilizeaza celule
![]() MEE2 Cap.2: Convertoare Analog-Numerice
MEE2 Cap.2: Convertoare Analog-Numerice
lucrând cu un tact cu 4 faze 4 porti)/ celula. Cu celulele respective se constituie
o arie ca n figura . Semnalul este mai înt i aditionat prin portile din grupul A.

Fig . Convertoare realizate cu dispozitive CCD
Acesta lucreaza n 6 tacte ca un registru de deplasare.
La fiecare tact principal, semnalul de intrare este esantionat si sarcina respectiva este introdusa în prima celula. Sarcina preexistenta n celula trece n 2 s.a.m.d.
Dupa 6 tacte informatia din celulele A este transferata n prima linie a zonei B.
În fine, dupa ce se umple si aceasta zona, sarcina din linia 3 a zonei B
este transferata n C.
Dupa umplerea memoriei informatia din C este extrasa cu un tact mai lent
si aplicata unui CAN cu aproximari succesive si stocata într-o memorie numerica.
Capacitatea totala de memorie este de 3 x 6 = 8 esantioane. Se utilizeaza doua asemenea dispozitive, rezultând o capacitate de 1056 esantioane de fapt utilizati pentru memoria de semnal sunt numai
|