Calculul erorilor de orientare a unei piese dupa doua suprafete cilindrice exterioare fata de o prisma fixa

valorile diametrelor celor doua suprafete cilindrice exterioare si unghiurile prismelor sunt diferite;

valorile diametrelor celor doua suprafete cilindrice exterioare sunt diferite, iar cele ale unghiurilor prismelor identice;

valorile diametrelor celor doua suprafete cilindrice exterioare, respectiv unghiurile prismelor sunt identice.

- diametrul suprafetei cilindrice exterioare S_1di si reprezinta dupa caz:

d_1min ; d₁ sau d_1max;

- diametrul suprafetei cilindrice exterioare S_2di si reprezinta dupa caz:

d_2min ; d₂ sau d_2max;

- distanta dintre axele celor doua suprafete cilindrice exterioare si reprezinta    dupa caz: A_min ; A sau A_max;

S_1di -e suprafata cilindrica exterioara S_1di si reprezinta dupa caz: S_1min ; S₁₀ sau S_1max;

S_2di - suprafata cilindrica exterioara S_2di si reprezinta dupa caz: S_2min ; S₂₀ sau S_2max.

Pentru determinarea operativa a valorilor coordonatelor ( si respectivsi ) si a erorilor de orientare a centrelor celor doua suprafete cilindrice exterioare ( si ), in baza relatiilor de calcul determinate mai sus, s-a elaborat un program de calcul pentru acestea (program care va fi prezentat la capitolul 5

Valorile calculate (rotunjite la trei zecimale) in cele trei ipoteze sunt trecute in figurile 3.26; 3.36 si 3.37, (au fost utilizate schemele si notatiile din figurile 3.21 … 3.25).

Din considerente de vizualizare sugestiva si o comparare usoara a graficelor s-a ales reprezentarea grafica color folosindu-se segmente de dreapta pentru unirea punctelor din grafic.

S-a ales aceasta reprezentare cu scopul de a putea urmari mai usor dispersia acestor coordonate fata de pozitia de referinta aleasa (pozitia 1) in variantele analizate si a permite totodata o analiza rapida a rezultatelor.

In continuare sunt prezentate detaliat erorile de orientare a unei piese dupa doua suprafete cilindrice exterioare fata de o prisma fixa in cele trei ipoteze propuse mai sus.

a) Diametrele celor doua suprafete cilindrice exterioare si unghiurile

prismelor au valori diferite.

Pentru piesa avuta in studiu (figura 3.7 prezentata la subcapitolul 3.2.3), in aceasta ipoteza, consideram urmatoarele valori:

Unghiurile prismelor sunt:

In baza relatiilor de calcul a valorilor coordonatelor ( si respectivsi ) si a erorilor de orientare a centrelor celor doua suprafete cilindrice exterioare ( si ) si introducad, in programul de calcul, valorile parametrilor de intrare pentru pozitiile extreme de orientare a pieselor (pozitii definite si analizate la subcapitolul 3.3.2), au rezultat valorile din figura 3.26 in baza carora au fost construite graficele din figurile 3.27; 3.28; 3.29; 3.30; 3.31 si 3.32.

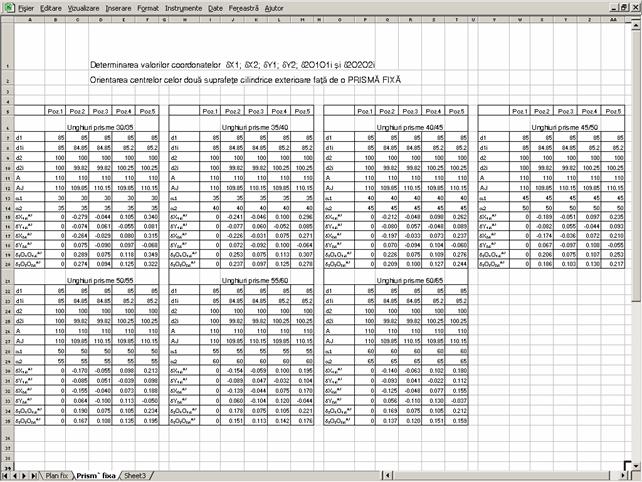
Fig.3.26. Imaginea ferestrei de lucru a calculatorului cu valorile coordonatelor si ale erorilor de orientare.

Unghiurile prismelor sunt variabile.

In figurile 3.27 … 3.32 sunt prezentate graficele pentru fiecare din coordonatele ( si respectivsi ) si pentru erorile de orientare a centrelor celor doua suprafete cilindrice exterioare ( si ) cu precizarea ca s-a dorit sa fie pusa in evidenta valoarea acestora fata de o pozitie de referinta (pozitia 1 care are valoarea egala cu 0).

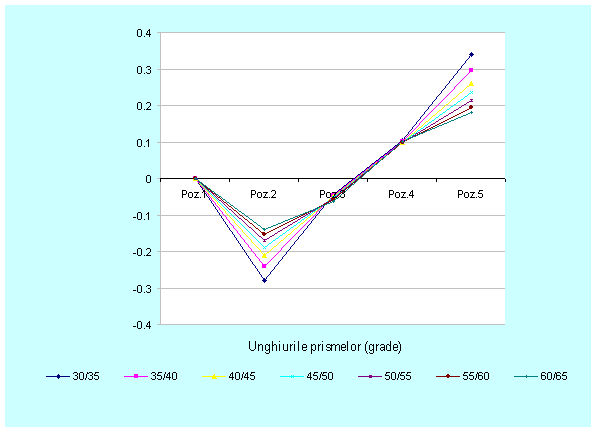
Fig. 3.27. Reprezentarea grafica a coordonatei .

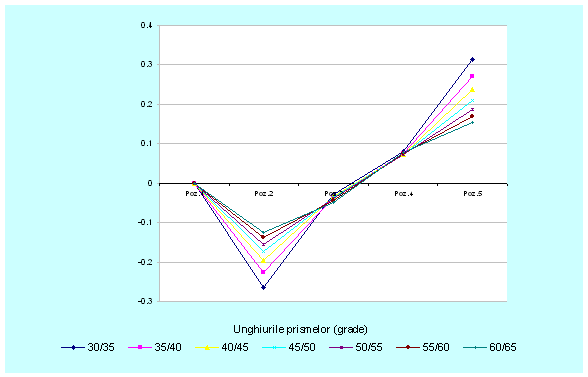
Fig. 3.28. Reprezentarea grafica a coordonatei

Din figurile 3.27 si 3.28 se observa ca valorile maxime ale coordonatelor respectiv pentru pozitiile omoloage au tendinta de descrestere odata cu cresterea unghiurilor celor doua prisme; valori mai mari se obtin in cazul pieselor executate la diametrele exterioare respectiv distanta dintre axe catre valoarea maxima.

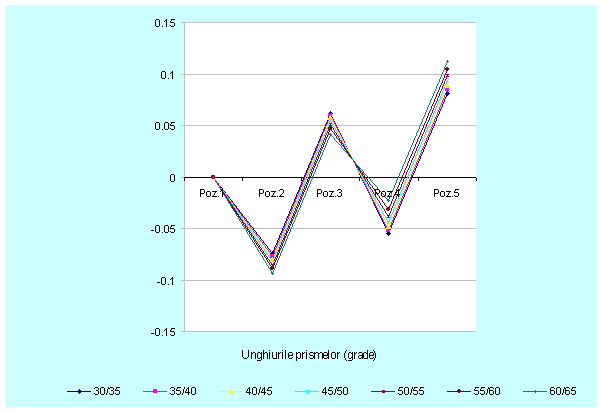
Fig. 3.29. Reprezentarea grafica a coordonatei

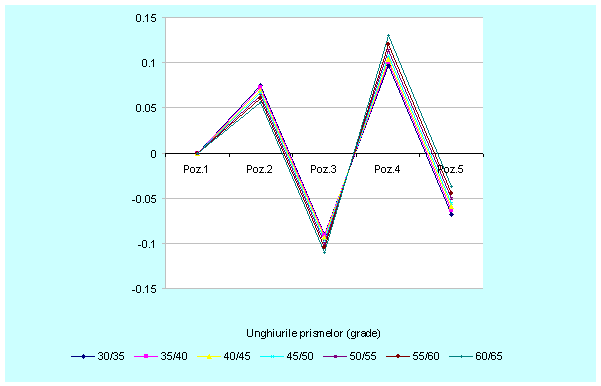
Fig. 3.30. Reprezentarea grafica a coordonatei.

Din figurile 3.29 si 3.30 rezulta ca valorile maxime ale coordonatelor respectiv pentru pozitiile omoloage au tendinta de crestere odata cu cresterea unghiurilor celor doua prisme; valori mai mari se obtin in cazul pieselor executate la diametrele exterioare respectiv distanta dintre axe catre valoarea maxima.

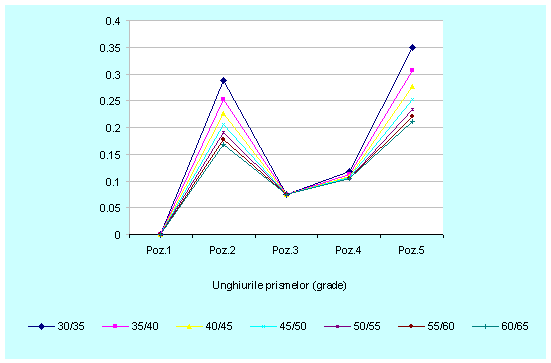
Fig. 3.31 . Reprezentarea grafica a erorii de orientare a centrului suprafetei S₁- .

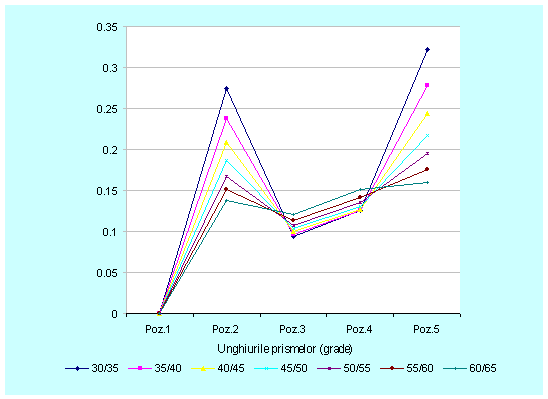
Fig. 3.32 . Reprezentarea grafica a erorii de orientare a centrului suprafetei S₂-.

Din figurile 3.31 si 3.32 rezulta ca valorile maxime ale erorii de orientare a centrelor celor doua suprafetei cilindrice exterioare respectiv pentru pozitiile omoloage au tendinta de descrestere odata cu cresterea unghiurilor celor doua prisme; valori mai mari se obtin in cazul pieselor executate la diametrele exterioare respectiv distanta dintre axe catre valoarea maxima.

In figura 3.33 sunt reprezentate, in plan, pozitiile extreme pe care le pot ocupa centrele celor doua suprafete cilindrice exterioare (O₁ respectiv O₂); pozitii care au fost reprezentate (la scara marita) in baza valorilor coordonatelor celor doua centre (valorile obtinute prin calcul care sunt trecute in figura 3.26).

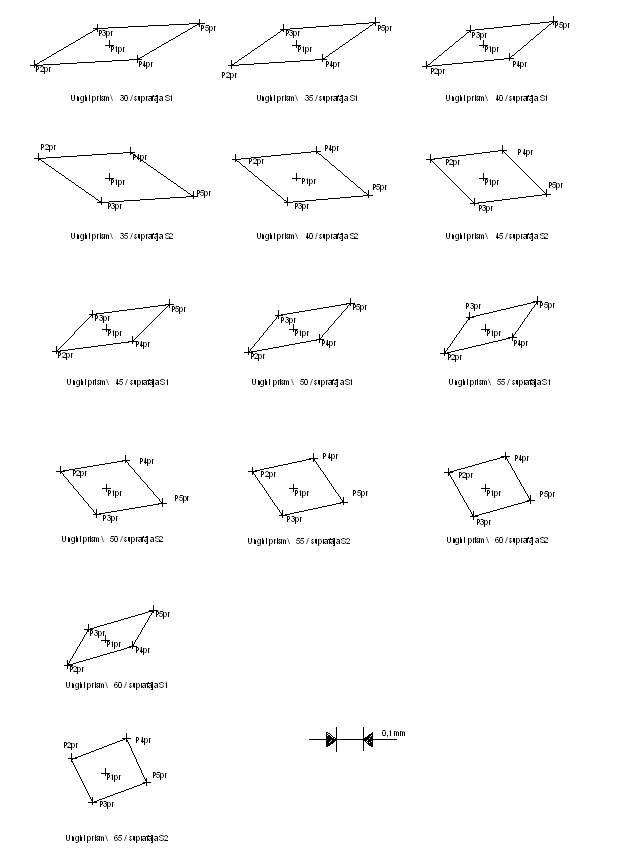
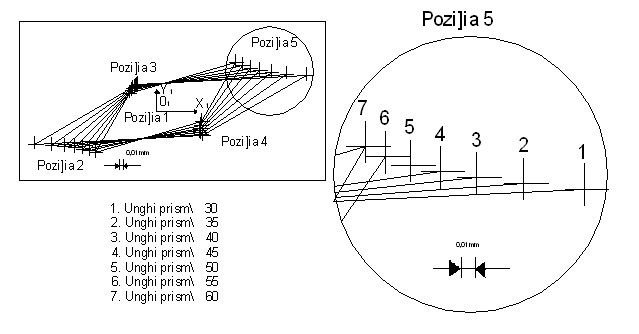
Fig. 3.34. Compararea pozitiilor pe care le poate ocupa centrul suprafetei cilindrice exterioare S₁ fata de o pozitie

de referinta (pozitia 1), la orientarea fata de o prisma fixa, in functie de variatia unghiurilor prismei.

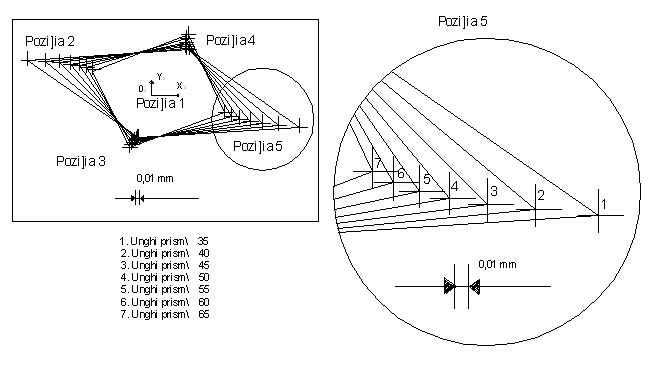
Fig. 3.35. Compararea pozitiilor pe care le poate ocupa centrul suprafetei cilindrice exterioare S_2difata de o pozitie

de referinta (pozitia 1), la orientarea fata de o prisma fixa, in functie de variatia unghiurilor prismelor.

Din figurile 3.33; 3.34 si 3.35 rezulta ca valorile maxime ale erorilor de orientare a centrelor celor doua suprafete cilindrice exterioare S_1di respectiv S_2di pentru pozitiile omoloage au tendinta de descrestere odata cu cresterea unghiurilor celor doua prisme.

b) Diametrelor celor doua suprafete cilindrice exterioare au valori diferite,

iar unghiurile prismelor au valori identice.

Pentru piesa propusa spre studiu (figura 3.7), in aceasta ipoteza, consideram urmatoarele valori:

Unghiurile prismelor sunt:

In baza relatiilor de calcul a valorilor coordonatelor ( si respectivsi ) si ale erorilor de orientare a centrelor celor doua suprafete cilindrice exterioare ( si ) si introducad, in programul de calcul, valorile parametrilor de intrare pentru pozitiile extreme de orientare a pieselor (pozitii definite si analizate la subcapitolul 3.3.2), au rezultat valorile din figura 3.36.

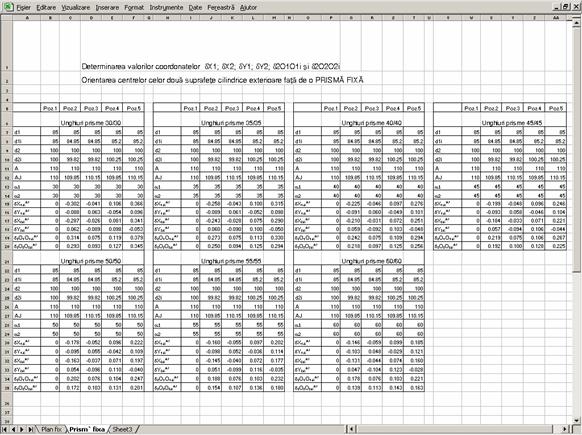
Fig.3.36. Imaginea ferestrei de lucru a calculatorului cu determinarea valorilor coordonatelor si ale erorilor de

orientare. Unghiurile prismelor sunt egale.

Din analiza valorilor prezentate in figura 3.18 se pot trage urmatoarele concluzii:

valorile maxime ale coordonatelor respectiv pentru pozitiile omoloage au tendinta de crestere odata cu cresterea valorilor unghiurilor celor doua prisme; valorile mai mari se obtin in cazul pieselor executate la diametrul exterior catre valoarea maxima;

valorile maxime ale erorilor de orientare a centrelor celor doua suprafete cilindrice exterioare respectiv pentru pozitiile omoloage au tendinta de descrestere odata cu cresterea valorilor unghiurilor celor doua prisme.

c) Diametrelor celor doua suprafete cilindrice exterioare si unghiurile prismelor au valori identice.

Pentru piesa propusa spre studiu (figura 3.7), in aceasta ipoteza, consideram urmatoarele valori:

Unghiurile prismei sunt:

In baza relatiilor de calcul a valorilor coordonatelor ( si respectivsi ) si ale erorilor de orientare a centrelor celor doua suprafete cilindrice exterioare ( si ) si introducad, in programul de calcul, valorile parametrilor de intrare pentru pozitiile extreme de orientare a pieselor (pozitii definite si analizate la subcapitolul 3.3.2), au rezultat valorile din figura 3.37.

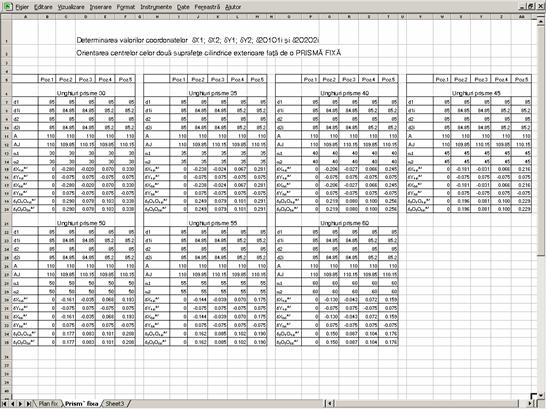
Fig.3.37. Imaginea ferestrei de lucru a calculatorului cu determinarea valorilor coordonatelor si ale erorilor de

orientare. Diametrele celor doua suprafete cilindrice exterioare si unghiurile prismelor au valori identice.

Din analiza valorilor prezentate in figura 3.37 se pot trage urmatoarele concluzii:

- valorile maxime ale coordonatelor respectiv pentru pozitiile omoloage

valorile coordonatelor respectiv pentru pozitiile omoloage sunt identice pentru ambele coordonate si raman constante odata cu cresterea unghiurilor prismelor;

valorile maxime ale erorilor de orientare a centrelor celor doua suprafete cilindrice exterioare respectiv pentru pozitiile omoloage sunt identice pentru ambele suprafete si are tendinta de descrestere.

3.3.4. Concluzii privind orientarea unei piese dupa doua suprafete cilindrice

exterioare fata de o prisma fixa.

A. Concluzii preliminare.

La aplicatiile facute pe piesa reprezentativa (figura 3.7) si in baza rezultatelor obtinute mai sus, pentru fiecare din cele trei ipoteze rezulta urmatoarele aspecte:

a) Diametrele celor doua suprafete cilindrice exterioare si unghiurile

prismelor au valori diferite.

Analizand valorile obtinute, pentru aplicatia facuta (figura 3.26; tabelele 3.5 si 3.6) si reprezentarile grafice (figurile 3.27; 3.28; 3.29; 3.30; 3.31; 3.32; 3.33; 3.34 si 3.35), pentru coordonatele ( respectiv si respectiv ) respectiv erorile de orientare a centrelor celor doua suprafete cilindrice exterioare ( respectiv _i) la orientarea pieselor dupa doua suprafete cilindrice exterioare fata de o prisma fixa pentru pozitiile analizate (poz. 2 … 5) raportate la pozitia de referinta (poz.1) la cresterea unghiurilor prismei rezulta:

Tabelul 3.5. Repartitia valorilor coordonatelor ;; si si ale erorilor de orientare

respectiv la orientarea fata de o prisma fixa (extras din figura 3.26).

Tabelul 3.6. Repartitia pozitiilor extreme ale centrelor celor doua suprafete cilindrice exterioare S_1di respectiv S_2di

la orientarea dupa doua suprafete cilindrice exterioare fata de o prisma fixa.

Concluzii:

Valoarea maxima a coordonatei are tendinta de descrestere cu cca. 93%;

Valoarea maxima a coordonatei are tendinta de descrestere cu cca. 106 %;

Valoarea maxima a coordonatei are tendinta de crestere cu cca. 32 %;

Valoarea maxima a coordonatei are tendinta de crestere cu cca. 29 %;

Valoarea maxima a erorii de orientare are tendinta de descrestere cu cca 65 %;

Valoarea maxima a erorii de orientareare tendinta de descrestere cu cca 102%;

Repartitia (aria acupata) centrelor celor doua suprafete cilindrice exterioare are tendinta de descrestere cu cca. 43%;

Perimetrul corespunzator pozitiilor extreme ale centrelor celor doua suprafete cilindrice exterioare are tendinta de descrestere cu cca. 38% .

b) Diametrele celor doua suprafete cilindrice exterioare au valori diferite,

iar unghiurile prismelor au valori identice.

Analizand valorile obtinute (figura 3.36 si tabelul 3.7), pentru aplicatia facuta, pentru coordonatele ( respectiv si respectiv ) respectiv erorile de orientare a centrelor celor doua suprafete cilindrice exterioare ( respectiv ) la orientarea pieselor dupa doua suprafete cilindrice exterioare fata de o prisma fixa pentru pozitiile analizate (poz. 2 … 5) raportate la pozitia de referinta (poz.1) la cresterea unghiurilor prismei rezulta:

Tabelul 3.7. Repartitia valorilor coordonatelor ;; si si ale erorilor de orientare

respectiv la orientarea fata de o prisma fixa (extras din figura 3.36).

Concluzii:

Din studiul efectuat se apreciaza ca:

Valoarea maxima a coordonatei are tendinta de descrestere cu cca 102 %;

Valoarea maxima a coordonatei are tendinta de descrestere cu cca 115 %;

Valoarea maxima a coordonatei are tendinta de crestere cu cca 22 %;

Valoarea maxima a coordonatei are tendinta de crestere cu cca 21 %;

Valoarea maxima a erorii de orientare are tendinta de descrestere cu cca 71%;

Valoarea maxima a erorii de orientare are tendinta de descrestere cu cca 112%.

c). Diametrele celor doua suprafete cilindrice exterioare si unghiurile

prismelor au valori identice.

Analizand valorile obtinute (figura 3.37 si tabelul 3.7), pentru aplicatia facuta, pentru coordonatele ( respectiv si respectiv ) respectiv erorile de orientare a centrelor celor doua suprafete cilindrice exterioare ( respectiv ) la orientarea pieselor dupa doua suprafete cilindrice exterioare fata de o prisma fixa pentru pozitiile analizate (poz. 2 … 5) raportate la pozitia de referinta (poz.1) la cresterea unghiurilor prismei rezulta:

Tabelul 3.8. Repartitia valorilor coordonatelor ;; si si ale erorilor de orientare

respectiv la orientarea fata de o prisma fixa (extras din figura 3.37).

Concluzii:

Pe baza celor prezentate rezultaca:

Valoarea maxima a coordonatelor respectiv este aceeasi pentru ambele coordonate si are tendinta de descrestere cu cca 111 %;

Valoarea maxima a coordonatei Y₁ respectiv Y₂ este identica pentru ambele coordonate si ramane constanta;

Valoarea maxima a erorii de orientare _O₁O_1i respectiv _O₂O_2i este identica pentru ambele suprafete si are tendinta de descrestere cu cca 93%.

B. Concluzii generale

Din analiza rezultatelor prezentate in figurile 3.26; 3.36 si 3.37 la orientarea unei piese dupa doua suprafete cilindrice exterioare fata de o prisma fixa se pot trage urmatoarele concluzii generale:

a)   Diferenta dintre valorile maxime ale erorilor de orientare a centrelor celor doua suprafete cilindrice exterioare respectiv pentru fiecare caz analizat (ipotezele a, b si c) ramane constanta (considerand valorile cu trei zecimale utilizate in costructia de masini) indiferent de marimea unghiurilor celor doua prisme;

b)   Diferenta dintre valorile maxime ale erorilor de orientare a centrelor celor doua suprafete cilindrice exterioare respectiv are tendinta de scadere pronuntata in cazul in care unghiurile prismelor au aceleasi valori (ipoteza b);

c)   Diferenta dintre valorile maxime ale erorilor de orientare a centrelor celor doua suprafete cilindrice exterioare respectiv in cazul in care cele doua suprafete cilindrice exterioare respectiv unghiurile celor doua prisme au valori egale este egala cu 0;

d)   Pentru valori ale unghiurilor celor doua prisme ( respectiv ) cuprinse in domeniul 40 … 50⁰ se obtin rezultate acceptate in practica in ceeace priveste valoarea erorilor de orientare a pieselor si permite utilizarea eficienta a robotilor industriali dotati cu dispozitive de preluare a pieselor avand o constructie simpla; nu este necesara in aceasta situatie dotarea robotilor cu dispozitive de apucare (dispozitive de complianta) care sa usureze preluarea pieselor orientate necorespunzator, fapt care ar conduce la costuri suplimentare; de asemenea pot fi realizate dispozitive pentru asamblarea foarte simple;

e)   Utilizarea rezultatelor privind determinarea erorilor de orientare servesc la alegerea solutiilor optime pentru realizarea dispozitivelor de alimentare cu piese din cadrul sistemelor automate de asamblare si poate constitui punctul de plecare la stabilirea solutiilor pentru elementele de orientare si apucare ale robotilor in cazul sistemelor de asamblare robotizate.

3.4. CONCLUZII GENERALE PRIVIND ORIENTAREA PIESELOR DUP| DOU| SUPRAFE}E CILINDRICE EXTERIOARE.

Pentru piesa reprezentativa (figura 3.7) propusa spre studiu s-au determinat valorilor coordonatelor ;;si respectiv ale erorile de orientare a centrelor celor doua suprafete cilindrice exterioare si respectiv si raportate la pozitia de referinta; valori determinate cu ajutorul relatiile de calcul a valorilor erorilor de orientare a centrelor celor doua suprafete cilindrice exterioare, in urmatoarele situatii:

- orientarea unei piese dupa doua suprafete cilindrice exterioare fata de un plan fix;

- orientarea unei piese dupa doua suprafete cilindrice exterioare fata de o prisma fixa.

Pentru a analiza comparativ influenta modului de orientare a unei piese dupa doua suprafete cilindrice exterioare in cele doua situatii in figura 3.38 sunt prezentate prin suprapunere la aceeasi scara pozitiile extreme ocupate de centrele celor doua suprafete, iar in baza concluziilor de la punctele 3.2.4 respectiv 3.3.4, a valorilor obtinute prin calcul la aplicatia facuta pe piesa reprezentativa la orientarea unei piese dupa doua suprafete cilindrice exterioare fata de un plan fix respectiv fata de o prisma fixa pentru cele trei ipoteze de lucru s-au intocmit tabelele 3.9; 3.10; 3.11; 3.12 si 3.13; rezulta:

a) Diametrele celor doua suprafete cilindrice exterioare si unghiurile

prismelor au valori diferite.

In tabelele 3.9; 3.10 si 3.11 s-au trecut valorile (utilizand mai multe zecimale) principalilor parametrii legati de orientarea unei piese dupa suprafetele cilindrice exterioare; aceasta pentru a putea pune in evidenta diferentele intre acestia pe anumite domenii de variatie ale diametrelor sau unghiurilor prismelor dupa cun urmeaza:

Tabelul 3.9. Repartitia valorilor coordonatelor ;;si si ale erorilor de orientare si

respectiv si raportate la pozitia de referinta la orientarea fata de un plan

fix comparativ cu orientarea fata de o prisma fixa.

Tabelul 3.10. Suprafata ocupata de pozitiile centrelor celor doua suprafete cilindrice exterioare S_1di respectiv S_2di la

orientarea dupa doua suprafete cilindrice exterioare fata de un plan fix comparativ cu orientarea fata

de o prisma fixa.

In figura 3.38 pentru comparare s-a reprezentat prin suprapunere la aceeasi scara pozitiile extreme pe care le pot acupa centrele celor doua suprafete cilindrice exterioare S_1di respectiv S_2di fata de pozitia de referinta (pozitia 1), la orientarea fata de un plan fix respective fata de o prisma fixa.

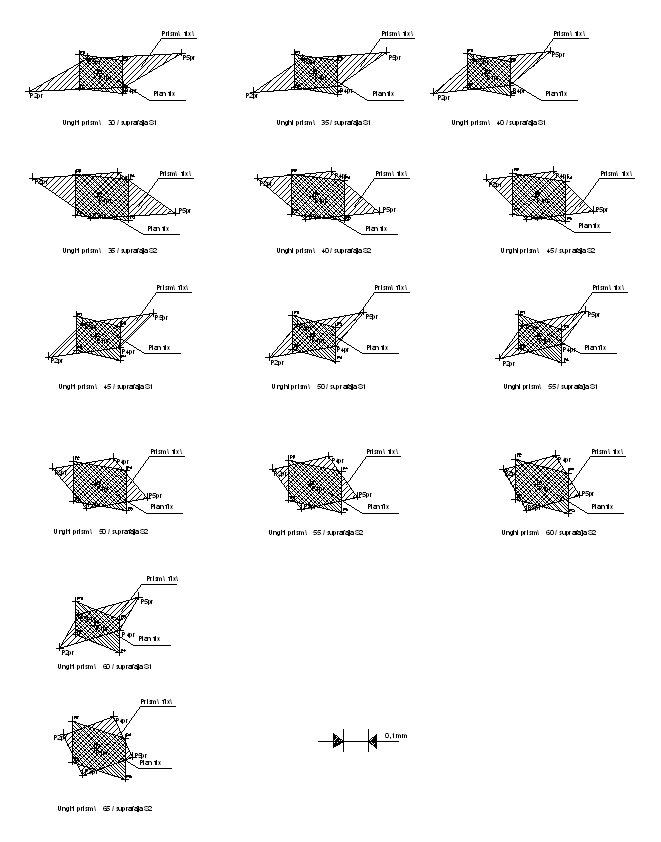
Fig 3.38. Comparare pozitiile pe care le pot acupa centrele celor doua suprafete cilindrice exterioare S_1di si S_2di.

Tabel 3.11. Perimetrul corespunzator pozitiilor extreme ale centrele celor doua suprafete cilindrice exterioare S_1di

respectiv S_2di la orientarea dupa doua suprafete cilindrice exterioare fata de un plan fix comparativ

cu orientarea fata de o prisma fixa.

Din analiza rezultatelor prezentate in tabelele 3.9; 3.10 si 3.11 si reprezentarile din figura 3.38 se pot trage urmatoarele concluzii

Valoarile maxime ale coordonatelor X₁ si X₂ au tendinta de crestere semnificativa in cazul orientarii fata de o prisma fixa comparativ cu orientarea fata de un plan fix la aceeasi valoarea a unghiurilor prismelor;

Valoarile maxime ale coordonatelor X₁ si X₂ au valori mai mari in cazul orientarii fata de o prisma fixa comparativ cu orientarea fata de un plan fix;

Valoarile maxime ale coordonatelor Y₁ si Y₂ au tendinta nesemnificativa de crestere sau descrestere (sub 2%) in cele doua cazuri;

Valoarile maxime ale erorilor de orientare O₁O_1i si O₁O_1i au tendinta de crestere semnificativa in cazul orientarii fata de o prisma fixa comparativ cu orientarea fata de un plan fix la aceeasi valoare a unghiurilor prismelor;

Valoarea maxima a erorilor de orientare O₂O_2i si O₂O_2i au tendinta de crestere la unghiuri mici ale prismelor si de descrestere la unghiuri mari ale prismelor;

La cresterea unghiurilor prismelor in cazul orientarii fata de o prisma fixa comparativ cu orientarea fata de un plan fix se manifesta o tendinta semnificativa de apropiere a valorilor coordonatelor, ale erorilor de orientare, ale ariei (suprafata ocupata de centrele celor doua suprafetelor) si perimetrului determinat de pozitiile extreme ale centrelor celor doua suprafete cilindrice exterioare.

b) Diametrele celor doua suprafete cilindrice exterioare au valori

diferite, iar unghiurile prismelor au valori identice.

In tabelul 3.12 s-au trecut valorile (cu multe zecimale) principalilor parametrii legati de orientarea unei piese dupa suprafetele cilindrice exterioare; aceasta pentru a putea pune in evidenta diferentele intre acestia pe anumite domenii de variatie ale diametrelor sau unghiurilor prismelor dupa cun urmeaza:

Tabelul 3.12. Repartitia valorilor coordonatelor ;;si si ale erorilor de orientare

si respectiv si raportate la pozitia de referinta la orientarea fata de un

plan fix comparativ cu orientarea fata de o prisma fixa.

Din analiza rezultatelor prezentate in tabelul 3.12 se pot trage urmatoarele concluzii

Valoarile maxime ale coordonatelor X₁ si X₂ au tendinta de crestere semnificativa in cazul orientarii fata de o prisma fixa comparativ cu orientarea fata de un plan fix la aceeasi valoarea a unghiurilor prismelor;

Valoarile maxime ale coordonatelor X₁ si X₂ au valori mai mari in cazul orientarii fata de o prisma fixa comparativ cu orientarea fata de un plan fix;

Valoarile maxime ale coordonatelor Y₁ si Y₂ au tendinta nesemnificativa de crestere sau descrestere (sub 1,5%);

Valoarile maxime ale erorilor de orientare O₁O_1i si O₁O_1i au tendinta de crestere semnificativa in cazul orientarii fata de o prisma fixa comparativ cu orientarea fata de un plan fix la aceeasi valoare a unghiurilor prismelor;

Valoarile maxime ale erorilor de orientare O₁O_1i si O₂O_2i au tendinta de crestere in cazul orientarii fata de o prisma fixa comparativ cu orientarea fata de un plan fix la aceeasi valoare a unghiurilor prismelor;

La cresterea unghiurilor prismelor in cazul orientarii fata de o prisma fixa comparativ cu orientarea fata de un plan fix se manifesta o tendinta semnificativa de apropiere a valoarea coordonatelor si a erorilor de orientare.

c) Diametrele celor doua suprafete cilindrice exterioare si unghiurile

prismelor au valori identice.

In tabelul 3.13 s-au trecut valorile (utilizand mai multe zecimale) principalilor parametrii legati de orientarea unei piese dupa suprafetele cilindrice exterioare; aceasta pentru a putea pune in evidenta diferentele intre acestia pe anumite domenii de variatie ale diametrelor sau unghiurilor prismelor dupa cun urmeaza:

Tabelul 3.13. Repartitia valorilor coordonatelor ;;si si ale erorilor de orientare si

respectiv si raportate la pozitia de referinta la orientarea fata de un plan

fix comparativ cu orientarea fata de o prisma fixa.

Din analiza rezultatelor prezentate in tabelul 3.13 se pot trage urmatoarele concluzii

Valoarile maxime ale coordonatelor X₁ si X₂ au tendinta de crestere semnificativa in cazul orientarii fata de o prisma fixa comparativ cu orientarea fata de un plan fix la aceeasi valoarea a unghiurilor prismelor;

Valoarile maxime ale coordonatelor X₁ si X₂ au valori mai mari in cazul orientarii fata de o prisma fixa comparativ cu orientarea fata de un plan fix;

Valoarile maxime ale coordonatelor Y₁ si Y₂ raman constante;

Valoarile maxime ale erorilor de orientare _O₁O_1i si _O₁O_1i respectiv _O₂O_2i si _O₂O_2i au tendinta de crestere in cazul orientarii fata de o prisma fixa comparativ cu orientarea fata de un plan fix la aceeasi valoare a unghiurilor prismelor;

La cresterea unghiurilor prismelor in cazul orientarii fata de o prisma fixa comparativ cu orientarea fata de un plan fix se manifesta o tendinta semnificativa de apropiere a valorilor coordonatelor si a erorilor de orientare.

Din analiza rezultatelor prezentate in acest capitol se pot trage urmatoarele concluzii generale

Diferenta dintre valorile maxime ale erorilor de orientare a centrelor celor doua suprafete cilindrice exterioare respectiv pentru fiecare caz analizat (ipotezele a, b si c) ramane constanta (considerand valorile de ordinul 0,001mm utilizate in constructia de masini) indiferent de marimea unghiurilor celor doua prisme;

Diferenta dintre valorile maxime ale erorilor de orientare a centrelor celor doua suprafete cilindrice exterioare respectiv are tendinta de scadere pronuntata in cazul in care unghiurile prismelor au aceleasi valori (ipoteza b);

Diferenta dintre valorile maxime ale erorilor de orientare a centrelor celor doua suprafete cilindrice exterioare respectiv in cazul in care cele doua suprafete cilin- drice exterioare respectiv unghiurile celor doua prisme au valori egale este egala cu 0;

Pentru valori ale unghiurilor celor doua prisme ( respectiv ) cuprinse in domeniul 40 … 50⁰ se obtin rezultate acceptate in practica in ceeace priveste marimea erorilor de orientare a pieselor fapt care permite utilizarea eficienta a robotilor industriali dotati doar cu dispozitive de prehensiune a pieselor avand o constructie simpla. In acest caz nu este necesara dotarea robotilor cu dispozitive de complianta care ar prelua abaterile de la orientarea necorespunzatoare a pieselor, fapt care conduce la economisirea costurilor suplimentare legate de echiparea robotului cu acest tip de dispozitiv. Totodata in cadrul sistemelor de alimentare in situatia aceasta se pot realiza dispozitive de asamblare simple si fiabile;

Relatiile stabilite pentru calculul valorilor coordonatelor ; ; si respectiv a valorilor erorilor de orientare a centrelor celor doua suprafete cilindrice exterioare ; ; si la orientarea unei piese dupa suprafetele cilindrice fata de un plan fix respectiv fata de o prisma fixa permit realizarea unor programe speciale de calcul a valorilor acestor parametrii care sa faca posibila o rezolvare rapida si precisa in scopul optimizarii solutiilor constructive ale dispozitivelor de alimentare cu piese, asa dupa cum se va prezenta in capitolele 5 si 6. Semnificatia notatiilor folosite este cea prezentata anterior

Utilizand rezultatele teoretice si practice obtinute s-a putut stabili solutia constructiva optima pentru un dispozitiv de alimentare cu piese pentru subansamblul „Zala interioara” din componenta lanturilor folosite in industria petroliera si totodata realizarea unor familii de masini automate de asamblat zale interioare la SC INDEPENDEN}A Sibiu; aplicatii care vor fi dezvoltate la capitolul 6;

Cunoasterea valorilor maxime ale erorilor de orientare a centrelor celor doua suprafete cilindrice exterioare face posibila adoptarea de solutii constructive adecvate pentru piesele conjugate care participa la procesul de asamblare (tesirea sau rotunjirea muchiilor suprafetelor de asamblare, etc);

Utilizarea rezultatelor privind determinarea erorilor de orientare serveste la alegerea solutiilor optime pentru realizarea dispozitivelor de alimentare cu piese din cadrul sistemelor automate de asamblare si poate constitui punctul de plecare la stabilirea solutiilor pentru elementele de orientare si apucare ale robotilor in cazul sistemelor de asamblare robotizate.