Documente online.
Zona de administrare documente. Fisierele tale
Am uitat parola x Creaza cont nou
 HomeExploreaza
upload
Upload




Calculul fiabilitatii motorului naval prin metoda eibull si urmarirea fiabilitatii in exploatare

tehnica mecanica


Calculul fiabilitãtii motorului naval prin metoda eibull si urmãrirea fiabilitãtii în exploatare

Se exemplificã aplicarea algoritmului anterior (paragraful 1.3) pentru un motor naval tip MAN L52/55A, cu alezajul D=520 mm, cursa S=550 mm.



Fiabilitatea motorului s-a estimat teoretic în urmãtoarele ipoteze:

rata defectãrilor este constantã, ipotezã valabilã în cazul unei exploatãri corecte, cu respectarea riguroasã a graficului de întretinere;

legea de distributie a defectelor este de tip Weibull;

fiabilitatea motorului, ca sistem complex, este caracterizatã de eficacitatea a trei subsisteme independente:

motorul propriu-zis (MP);

sistemul de pornire (SP);

sistemul de comandã de la distantã (SCD).

Beneficiarul impune o fiabilitate de minim 7% pentru 200 ore de functionare. Pentru estimarea fiabilitãtii, s-au folosit informatii prelevate de pe esantioane aflate sub observatie în exploatare: s-au avut sub observatie N=3 motoare L52/55A, exploatate în conditii identice. Timpii înregistrati de functionare pânã la prima defectare au fost: (cãdere accidentalã).

Legea de repartitie Weibull se caracterizeazã prin urmãtoarele:

densitatea de repartitie


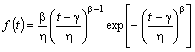, (1)


unde:

-parametru de formã; în general ; pentru se obtine repartitia Gauss;

-parametru de scarã;

-parametru de localizare.

functia de repartitie


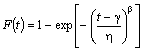; (2)


Etape de calcul al fiabilitãtii sunt:

se alege, uzual:


; (3)


se determinã prin metoda asimilãrii maxime (metodã graficã):

E 1

E 2

E 3

E 4

E 5

E 6

E 7

E 8

E 9

E 10

E 11

E 12

E 13

E 14

E 15

E 16

E 17

E 18

E 19

E 20

E 21

E 22

E 23

E 24

E 25

E 26

E 27

E 28

  . (4)


Pentru aceasta, se considerã functiile:


(5)


Se prezintã grafic functiile si , la intersectia lor determinându-se parametrul ; este, evident, posibilã si utilizarea metodelor numerice de calcul pentru rezolvarea ecuatiei (4); metoda graficã este ilustratã în figura 1.

Pentru cazul particular prezentat, se obtine solutia , care verificã egalitatea:

se determinã din relatia:


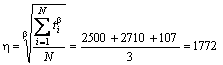. (6)


se reformuleazã functia de repartitie (2):


. (7)

se expliciteazã functia de fiabilitate prin intermediul lui (7):


. (8)


Asa cum s-a arãtat însã:


. (9)


Luând rata defectãrilor (conform primei ipoteze) si considerând momentul initial al observatiilor , se obtine:


. (10)


se determinã rata defectãrilor, prin comparatia dintre (8) si (10):


(11)


se precizeazã rata defectãrilor (din experienta exploatãrii unor produse similare), fiabilitatea pentru 200 ore de functionare si media timpului de bunã functionare pentru fiecare subsistem (conform celei de-a treia ipoteze):



PROGRAM DE URMÃRIRE A FIABILITÃTII

Fisa de regim

Se completeazã zilnic în timpul functionãrii motorului


Data

Ora

Indicator contor ture

Pozitia*

Obs.































* Se trece pozitia medie a tijelor de comandã de la pompele de injectie, pozitie cu care s-a mers în ziua respectivã.




Prezenta fisã serveste exclusiv pentru studii de fiabilitate. Datele înscrise în ea au caracter confidential si se vor transmite furnizorului motorului, fiind interzisã transmiterea lor cãtre alte persoane sau societãti.

Semnãtura Mecanicului ªef:

;

E 1

E    2

E    3

E    4

E    5

E    6

E    7

E    8

E    9

E 10

E 11

E 12

E 13

E 14

E 15

E 16

E 17

E 18

E 19

E 20

E 21

E 22

E 23

E 24

E 25

E 26

E 27

E 28

 



PROGRAM DE URMÃRIRE A FIABILITÃTII

Fisa cu uleiuri

Se completeazã la fiecare alimentare cu ulei pe baza analizei uleiului din rezervor


Data

Portul

Firma.

Denumirea

TBN

Vâsc. la 50oC

[oE]

Indice de vâsc.

Continut apã

Obs.


Constanta

SHELL

GADINIA 40





Amsterdam

SHELL

GADINIA 40




Prezenta fisã serveste exclusiv pentru studii de fiabilitate. Datele înscrise în ea au caracter confidential si se vor transmite furnizorului motorului, fiind interzisã transmiterea lor cãtre alte persoane sau societãti.

Semnãtura Mecanicului ªef:


E 1

E 2

E 3

E 4

E 5

E 6

E 7

E 8

E 9

E 10

E 11

E 12

E 13

E 14

E 15

E 16

E 17

E 18

E 19

E 20

E 21

E 22

E 23

E 24

E 25

E 26

E 27

E 28

 
Fisa cu combustibili

Se completeazã la fiecare alimentare cu combustibil


Data

Portul

Tip comb.

Dens.

[kg/dm3]

Vâsc.

Sulf

Vanadiu

Cenusã

Cocs

Obs.


Constanta

DFO

HFO

2.5oE

1500 sec. Redw.I







Apã

Amsterdam

HFO

3400 sec. Redw I



Prezenta fisã serveste exclusiv pentru studii de fiabilitate. Datele înscrise în ea au caracter confidential si se vor transmite furnizorului motorului, fiind interzisã transmiterea lor cãtre alte persoane sau societãti.

Semnãtura Mecanicului ªef:




Fisa cu defectiuni


Data

Defectiunea

Cauza probabilã.

Mãsuri

Durata indisponib.

[ore]


Injector cil. 2 blocat

Murdãrie în combustibil

S-a înlocuit injectorul



Electroventil R570/3 defect

Termocuplu gaze evacuare cil. 3 defect-

S-a ars bobinajul

A fost înlocuit electroventilul


Se va înlocui la prima oprire



Revizie 2.500 ore:

joc mare supapa admisie cil. 3;

sertar pornire cil. 7 blocat;

presiune mare de ardere la cil. 1 (131 bar).




murdãrie în aer;


dereglarea avan-sului la injectie.

s-a reglat jocul;

s-a demontat si s-a curãtat sertarul;

s-a deplasat cama pentru reducerea avansului, cu o rotatie a surubului de fixare; dupã reglare s-a mãsurat o presiune de 125 bar la regimul nominal


Prezenta fisã serveste exclusiv pentru studii de fiabilitate. Datele înscrise în ea au caracter confidential si se vor transmite furnizorului motorului, fiind interzisã transmiterea lor cãtre alte persoane sau societãti.

Semnãtura Mecanicului ªef


E 1

E    2

E    3

E    4

E    5

E    6

E    7

E    8

E    9

E 10

E 11

E 12

E 13

E 14

E 15

E 16

E 17

E 18

E 19

E 20

E 21

E 22

E 23

E 24

E 25

E 26

E 27

E 28

  Acest program implicã completarea regulatã de cãtre personalul de exploatare a patru tipuri de fise, conform modelelor din norma tehnicã internã si anume:

fisa de regim;

fisa cu combustibili;

fisa cu uleiuri;

fisa cu defectiuni

si presupune respectarea riguroasã a graficului de revizii; programul de urmãrire a fiabilitãtii este ilustrat în tabelele anterioare.


1.6. Actiunea simultanã a defectelor accidentale si a celor de uzurã în studiul fiabilitãtii echipamentelor navale

Cu tot caracterul ei general, caracteristica de viatã depinde de domeniul specific al produsului respectiv. Astfel, dacã produsele electronice se manifestã de obicei printr-o regiune întinsã a vietii utile, având , nu tot astfel se comportã produsele mecanice, la care aceastã regiune este mult mai redusã, trecerea de la regiunea de rodaj la cea de uzurã fãcându-se mult mai rapid. Pe de altã parte, complexitatea actualã a produselor împiedicã o departajare categoricã a în produse pur electronice, electrotehnice sau mecanice, astfel încât tehnologiile specifice fiecãrui domeniu impun de cele mai multe ori tratarea fiabilitãtii din mai multe puncte de vedere.

Astfel, dacã luãm în consideratie evenimentele: AC-produsul nu se defecteazã de-a lungul duratei , datoritã defectiunilor accidentale (regiunea vietii utile); UZ-produsul nu se defecteazã de-a lungul duratei , datoritã defectiunilor sistematice (regiunea de uzurã), atunci evenimentul E caracterizat prin intersectia celor douã multimi:


(12)


corespunde conditiei sã nu se defecteze de-a lungul duratei , nici datoritã defectelor accidentale, nici datoritã celor cu caracter sistematic. Probabilitatea acestui eveniment este:




, (13)


evenimentele AC si UZ fiind independente; probabilitãtile de mai sus corespund functiilor proprii celor douã regiuni ale caracteristicii de viatã, adicã:


. (14)


Tinând seama cã:


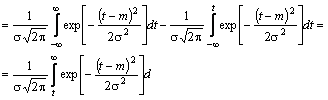(15)


deci:


. (16)


Notând: (din distributia Poisson) si , unde m este valoarea medie a distributiei gaussiene, ultima relatie se poate calcula pe baza functiilor tabelate exponential negativã si normal normatã: si , deci:


. (17)


Reprezentarea graficã a fiabilitãtii este redatã în continuare în figura 1.

S-a presupus, în cele anterioare, cã dispozitivul contine atât componente mecanice, cât si electrice.

Vom reconsidera acelasi caz, în care însã complexitatea de mai sus nu are un caracter omogen, din punct de vedere al vârstei componentelor, unele dintre ele cumulând un timp calendaristic mai mare si diferit de la caz la caz, datoritã unor reparatii necorespunzãtoare, fie înlocuirii cu componente la rândul lor uzate. Suntem în cazul fiabilitãtii multiplu conditionate. Însã, în relatia fiabilitãtii datã de legea de tip exponential, viata anterioarã a produsului, , nu se regãseste; în schimb, în cazul legii de uzurã, fiabilitatea depinde de timpul calendaristic .

Deci fiabilitatea specificã influentei comune a defectelor de tip accidental si de uzurã (sistematic) devine:


, (18)


sau, cu folosirea valorilor normate:


, (19)

unde:


. (20)

În cazul particular (dispozitiv nou), .

Datoritã timpului calendaristic, între durata medie neconditionatã m si cea conditionatã în cadrul noii misiuni tehnice este relatia:


, (21)


astfel încât graficul relatiei (18) va fi obtinut din cel pentru (relatia (14)) printr-o rototranslatie (fig. 2).

Generalizând cele de mai sus, când, datoritã unui numãr de N cauze, de naturã accidentalã, cât si sistematicã, fiabilitatea întregului complex depinde de produsul fiabilitãtilor elementelor ce intrã în componenta ansamblului, obtinem relatia generalã:


, (22)


sau, cu valori normate:


, (23)


unde:


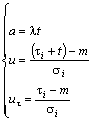, (24)


corespunde vârstei diferitelor subansamble si componente ale sale.

În cazul în care toate componentele sunt identice si noi (identitatea este caracteristicã echipamentelor electronice), avem , deci:


, (25)


N fiind numãrul elementelor componente ale sistemului. Tinând cont de aspectul exponential al legii defectelor accidentale, se obtine:


. (26)


Dacã excludem probabilitatea manifestãrii defectelor cu caracter sistematic, fiabilitatea echipamentului este legatã de fiabilitatea componentelor care îl alcãtuiesc:

. (27)


E 1

E 2

E 3

E 4

E 5

E 6

E 7

E 8

E 9

E 10

E 11

E 12

E 13

E 14

E 15

E 16

E 17

E 18

E 19

E 20

E 21

E 22

E 23

E 24

E 25

E 26

E 27

E 28

  În cazul când sistemul este compus din n tipuri de elemente identice, fiecare tip în numãr de câte , cu intensitatea sa defectare , relatia generalã a fiabilitãtii echipamentului, în ipoteza legii exponentiale a defectelor este:


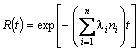, (28)


deci se regãseste relatia deja cunoscutã.








































E 1

E    2

E    3

E    4

E    5

E    6

E    7

E    8

E    9

E 10

E 11

E 12

E 13

E 14

E 15

E 16

E 17

E 18

E 19

E 20

E 21

E 22

E 23

E 24

E 25

E 26

E 27

E 28

 

Fig. 2
 

Fig. 1
 























































Document Info


Accesari: 2107
Apreciat: hand-up

Comenteaza documentul:

Nu esti inregistrat
Trebuie sa fii utilizator inregistrat pentru a putea comenta

Creaza cont nou

A fost util?

Daca documentul a fost util si crezi ca merita
sa adaugi un link catre el la tine in site


in pagina web a site-ului tau.



eCoduri.com - coduri postale, contabile, CAEN sau bancare

Politica de confidentialitate | Termenii si conditii de utilizare




Copyright © Contact (SCRIGROUP Int. 2025 )