Calculul recursiv al coeficientilor functiei generatoare

Calculul recursiv al coeficientilor functiei generatoare

Fie o retea închisa de calculatoare cu N noduri de retea si n tranzactii la prelucrare si fie g(t) functia generatoare a sa.

g(t)= (1+x_it+t²

5.2.4.1.2.a Algoritm pentru determinarea coeficientilor functiei generatoare [17]

Efectuând produsul în functia generatoare obtinem :

g(t)=1+tG(1)+t²G(2)+.+G(j)+.

Construim recursiv urmatorul sir de functii (g_i(t))_i=:

g₁(t)=x₁(t)= 1+x₁t+t²

g₂(t)= g₁(t)x₂(t)=g₁(t) =g₁(t)[1+]=

=g₁(t)[1+]=g₁(t)[1+]=

=g₁(t)+ =g₁(t)+

g_i(t)= g_i-1(t)

Cum =1 si astfel

g_i(t)=g_i-1(t)[]=g_i-1(t)+ =g_i-1(t)+

Astfel am construit sirul (g_i(t)) _i= , unde :

g₁(t)=x₁(t),

g_i(t)=g_i-1(t)+ , i=.

Se observa ca

g_N(t)=g_N-1(t)x_N(t)=g(t)

si astfel coeficientii functiei generatoarte g sunt coeficientii functiei g_N.

Notam cu G_i(j) coeficientul lui t^j din g_i(t).

Astfel G(j)=G_N(j), pentru orice j1.

Din relatia de definitie a lui g_i(t) se observa ca :

G_i(j)= G_i-1(j)+x_i G_i(j-1) j si i

Aceasta relatie se obtine identificând coeficientul lui t^j din relatia lui g_i(t).

Formula gasita permite obtinerea unui algoritm simplu si eficient pentru calcularea coeficientilor G_i(j) si în particlar pentru calculul coeficientilor G(j)=G_N(j), j0 ai functiei generatoare a relatiei.

Analizând mai atent formula de mai sus observam :

Pentru i=, G_i(0)=1 (coeficientul lui t⁰ din g_i(t))

Pentru i=2 G₂(j)=G₁(j)+x₂G₂(j-1)

Rezulta G₂(j)=+x₂G₂(j-1)

Se obtine o ecuatie neomogena de ordinul 1 cu coeficienti constanti ecuatie a carei solutie este :

G₂(j)

Pentru aceasta s-a folosit si conditia initiala G₂(0)=1.

Pentru j=1, G_i(1)=G_i-1(1)+x_iG_i(0) dar G_i(0)=1 si astfel G_i(1)= G_i-1(1)+x_i de unde prin inserare ? ? ? de la 2 la i obtinem

G_i(1)=

5.2.4.1.2.b Implementarea algoritmului

Pornim de la relatia de recurenta

P1. Definim o matrice G de ordin (n+1)N, în care G(j,i)=(j).

P2. Prima linie din G are toate elementele 1, pentru ca G_i(0)=1, i

P3. Coloana 1 din G are pe locul j elementul , j=, conform observatiei O2.

P4. Pentru j= si i= elementele G(j,i) ale matricei G se calculeaza pornind de la G(1,2) si folosind relatiile :

G(j,i)=(j), unde (j)=(j)+(j-1)

de unde rezulta G(j,i)=+   G(j-1,i)

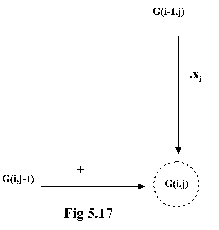
Astfel : "Înmultind elementul G(j-1,i) de deasupra lui G(j,i) cu si rezultatul îl adunam la elementul G(j,i-1) din stânga lui G(j,i) ; ceea ce obtinem, punem pe locul G(j,i) din matrice", ca în figura 5.17.

P5. Elementele ultimei coloane din G, adica G(j,N)=G_N(j), j=, sunt coeficientii lui t^j din functia generatoare, deci G(j)=G_N(j)=G(j,N), j=

Se observa ca formula implementata în acest algoritm permite calculul lui pentru orice i=.

g_i(t)=( 1+x₁t+t²+.)(1+x₂t+t²+.).(1+x_it+t²

Matricea G are forma :

5.2.4.1.3 Calculul direct al coeficientilor G(j) ai functiei generatoare [17].

Pornim de la

g(t)===

Astfel

g(t)=1+tG(1)+t²G(2)+.=

Pentru transformarea lui g(t), de mai sus, în sume de fractii simple apar doua cazuri :

Cazul 1. ij, x_jx_i (adica timpii de prelucrare ponderati sunt distincti)

Cazul 2. ij, astfel încât x_i=x_j (timpi de prelucrare multipli).

În primul caz  putem scrie

g(t)=,

unde coeficientii A_k se obtin astfel :

=/1-x_jt si apoi luam t=A_j=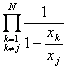

Deci A_k=

Astfel

g(t)= ==

dar g(t)=, si prin identificare obtinem :

G(j) ,

deci G(j) este o functie liniara în puterea j a variabilelor x₁,x₂,.,x_{N .}

G(j)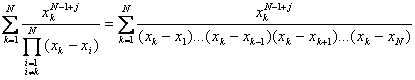

În cazul 2 (timpi de prelucrare multipli)  avem de dezvoltat în sume de fractii simple, functii cu poli multipli.

În cazul polilor multipli functia rationala se scrie

=,

unde s_k este radacina multipla de ordinul m_k a polinomului B(s) pentru k=

În acest caz

=

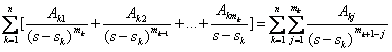
Aici coeficientii A_kj sunt dati de formula:

A_kj=, si

Observam ca s=

Exemplul 5.2.4.3. [17]. Fie

B(s)=s³+6s²+7s+4=0

Astfel

=

unde

A₁₁=

A₁₂=

A₂=

Astfel :

Exemplul 5.2.4.4 [17]. Se da o retea de calculatoare locala cu 4 noduri de prelucrare în care timpii ponderati de prelucrare sunt : x₁=3.25, x₂=4.75, x₃=4.75, x₄=5.30.

Pentru evaluarea performantelor acestei retele de calculatoare, trebuie sa determinam coeficientii functiei generatoare asociate,

g(t)=

Dezvoltând în sume de fractii simple avem

g(t)=, unde coeficientii se obtin prin :

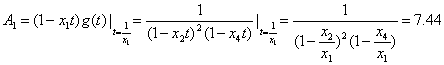
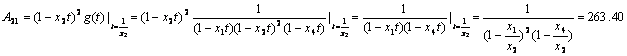
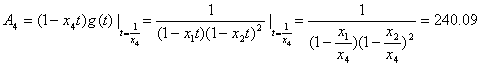
Prin urmare A₁=7.44, A₂₁=263.40, A₂₂=1553.89, A₄=240.09

Cu aceasta

g(t)=

Pornind de aici se pot determina coeficientii G(j) ai lui t^j.

5.2.4.1.4 Solutia generala pentru o clasa de tranzitii [17]

Fie g(t)=. Presupunem ca numitorul are p radacini multiple , cu ordinul de multiplicitate m_k1, k= si n-p radacini simple. Rearanjam factorii de la numitor astfel încât radacinile simple sa fie la început iar radacinile multiple sa fie la sfârsit ; aici n este numarul radacinilor distincte. Astfel N=n-p+.

Observatia 5.2.4.5.

Daca f(t)= atunci f(t)=,

unde :

f (t)=n(1-t)^-n-1, f (t)=n(n+1)(1-t)^-n-2,.,

., f ^j(t)=n(n+1).(n+j-1)(1-t)^-n-j=.

Astfel f ⁱ(0)= si deci

f(t)=.

Prin urmare

Se observa ca:

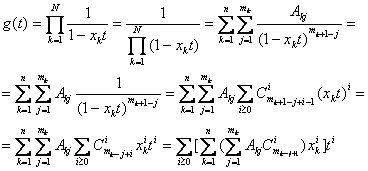
Cum g(t)=, prin identificare obtinem

G(i)=

Observam ca pentru m_k=1 j=1 si deci .