In conformitate cu definitiile prezentate in paragraful I 5.2 campurile magnetice se pot clasifica in doua categorii:
Ø campuri magnetice de dispersie ale caror linii de camp se inchid numai in jurul conductoarelor bobinei inductoare care creeaza campul
Ø campuri magnetice utile ale caror linii de camp se inchid astfel incat cuprind atat conductoare ale infasurarii inductoare cat si conductoare ale infasurarii indusului
Campul magnetic util realizeaza cuplajul magnetic dintre infasurarea inductoare si infasurarea indusului, iar in cazul concret al masinilor electrice in constructie circulara campul magnetic util se inchide, in majoritate, prin intrefier de la o armatura la cealalta.
In conformitate cu definitiile prezentate in paragraful I 5.3, liniile campului magnetic util sunt linii ale campului magnetic mutual.
Asa cum s-a prezentat in paragraful I 5.1 si paragraful III 2, in anumite cazuri practice conductoarele din care sunt executate infasurarile se dispun in crestaturi care au deschidere spre intrefier - vezi figurile 1.11 b, c, f si 3.5 a. In comparatie cu diametrul armaturii deschiderea crestaturii spre intrefier, ca si latimea crestaturii sunt mult mai mici.
in cazuri practice se idealizeaza constructia, neglijandu-se latimea si deschiderea crestaturilor - vezi figura
Ipoteza neglijarii dimensiunilor laturilor de bobina asezate in crestaturi, respectiv a dimensiunilor crestaturii, (vezi figurile 3.8 a si d) conduce la urmatoarele efecte:
Ø se inlocuiesc armaturile reale (vezi figura 3.8 a) cu doua armaturi netede, fara crestaturi (vezi figura.3.8 e);
Ø conductoarele sunt filiforme si sunt asezate in intrefier, in axa crestaturilor reale (vezi figura 3.8 d);
Ø se neglijeaza campul de dispersie;
Ø
intrefierul de largime ![]() dintre armaturile
reale (vezi figura 3.8 a) se inlocuieste cu un intrefier echivalent de largime majorata
dintre armaturile
reale (vezi figura 3.8 a) se inlocuieste cu un intrefier echivalent de largime majorata ![]() (vezi figura..2.4.d);
(vezi figura..2.4.d);
Ø inductia magnetica din intrefier este constanta spatial (vezi figura 3.8 f);
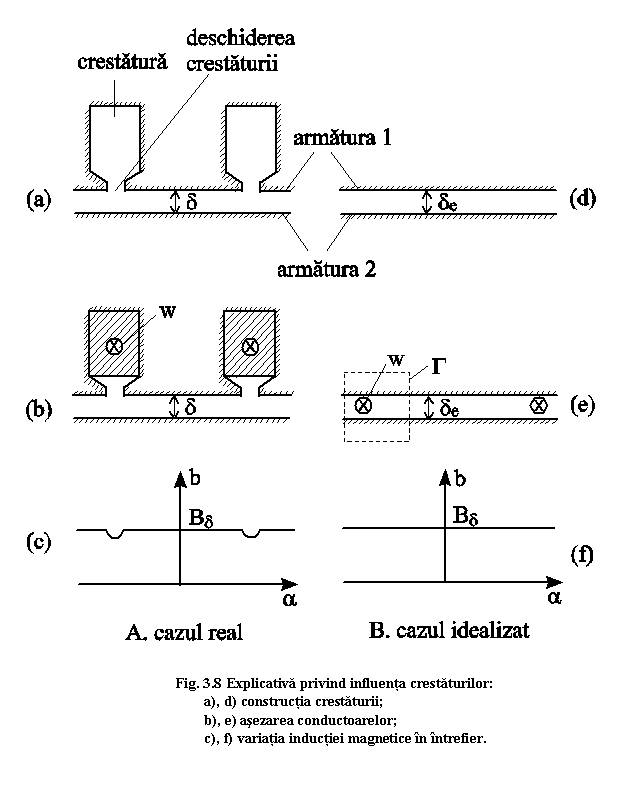
Campurile magnetice din intrefierul unei masini electrice se vor analiza pe o masina echivalenta care are urmatoarele proprietati:
Ø intrefierul este constant
axial si radial, si egal cu intrefierul echivalent.![]() ;
;
Ø conductoarele sunt filiforme si asezate, separat, in intrefier pe suprafata armaturii;
Ø se considera efectele de capat
prin folosirea lungimii ideale ![]() ;
;
Ø se neglijeaza campul magnetic de dispersie, pentru ca nu mai exista dispersiile impuse de existenta crestaturii a capetelor de bobina.
Descrierea campului
magnetic din masina - armaturi si intrefier - se poate face cu ajutorul vectorului inductie magnetica
![]() , respectiv cu ajutorul vectorului intensitatii
campului magnetic
, respectiv cu ajutorul vectorului intensitatii
campului magnetic ![]() , intre cei doi
vectori existand dependenta precizata de legea legaturii in camp magnetic:
, intre cei doi
vectori existand dependenta precizata de legea legaturii in camp magnetic:
![]()
exprimata in cazul absentei magnetilor permanenti.
Valoarea permeabilitatii magnetice ![]() depinde de natura
mediului material in care se analizeaza campul.
depinde de natura
mediului material in care se analizeaza campul.
Intensitatea campului magnetic este legata de sursele de camp - repartitiile de curent - prin legea circuitului magnetic:
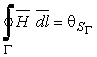
Curba inchisa ![]() trece, in mod normal,
prin medii cu proprietati magnetice diferite: aer si material feromagnetic -
vezi figura 3.8 e. Ca urmare, integrala curbilinie se poate descompune intr-o
suma de termeni corespunzatori mediilor prin care trece curba
trece, in mod normal,
prin medii cu proprietati magnetice diferite: aer si material feromagnetic -
vezi figura 3.8 e. Ca urmare, integrala curbilinie se poate descompune intr-o
suma de termeni corespunzatori mediilor prin care trece curba ![]() .
.
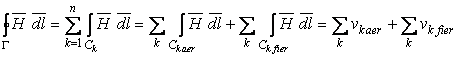
S-a notat cu 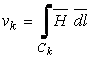 tensiunea magnetica de-a lungul portiunii
tensiunea magnetica de-a lungul portiunii ![]() a conturului
a conturului ![]() , iar
, iar ![]() este elementul de
linie.
este elementul de
linie.
Solenatia ![]() imbratisata de
conturul
imbratisata de
conturul ![]() poate fi exprimata in
functie de densitatea
poate fi exprimata in
functie de densitatea ![]() de curent respectiv in
functie de curentii care strabat conductoare repartizate discret la periferia
armaturilor
de curent respectiv in
functie de curentii care strabat conductoare repartizate discret la periferia
armaturilor
![]()
unde ![]() este elementul de
arie.
este elementul de
arie.
In cazul in care
conturul![]() , de lungime
, de lungime ![]() , este linie de camp si in lungul acesteia campul magnetic
are intensitatea constanta
, este linie de camp si in lungul acesteia campul magnetic
are intensitatea constanta ![]() se poate scrie:
se poate scrie:
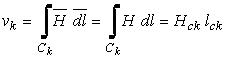 (3.5 a)
(3.5 a)
relatie care permite, pe portiuni, analiza campului cu ajutorul tensiunii magnetice:
![]() si
si ![]() (3.5
b)
(3.5
b)
Analiza campurilor magnetice din intrefier, care sunt campuri magnetice utile, se efectueaza in anumite ipoteze simplificatoare, care nu afecteaza sensibil rezultatele obtinute:
Se
neglijeaza reluctanta magnetica a portiunilor din intrefier a circuitului
magnetic, considerandu-se permeabilitatea magnetica ![]() . Astfel intreaga energie magnetica este localizata in
intrefier, iar miezul magnetic contribuie numai la ghidarea liniilor campului
magnetic.
. Astfel intreaga energie magnetica este localizata in
intrefier, iar miezul magnetic contribuie numai la ghidarea liniilor campului
magnetic.
Se neglijeaza pierderile din miezul magnetic datorate curentilor turbionari si histerezisului.
Armaturile
se considera netede, iar intrefierul este egal cu intrefierul echivalent ![]() .
.
Se neglijeaza campul magnetic de dispersie.
Infasurarile sunt executate din conductoare filiforme si sunt dispuse pe periferia armaturilor, spre intrefier.
Se considera ca infasurarile sunt alimentate cu curenti constanti sau sinusoidali in timp.
In conditiile enumerate, in intrefier, se poate aplica principiul suprapunerii efectelor, iar liniile de camp sunt radiale. Din acest motiv linia de camp este egala largimii intrefierului
![]()
iar
pentru coordonata spatiala ![]() expresia inductiei
magnetice este - vezi ecuatia (3.5.b):
expresia inductiei
magnetice este - vezi ecuatia (3.5.b):
III 3.1. Sursele campului magnetic util
Asa cum s-a demonstrat in capitolul I, sursele campului magnetic sunt infasurarile parcurse de curent electric sau magnetii permanenti. In constructia convertoarelor electrice se folosesc trei tipuri constructive de infasurari: infasurari repartizate, uniform repartizate si infasurari concentrate - vezi paragraful III.2 si figura 3.5. La randul lor, infasurarile repartizate se clasifica in infasurari monofazate si infasurari polifazate.
Cunoasterea repartitiei spirelor infasurarilor, determina tensiunea magnetica din intrefier, cu ajutorul careia, conform expresiei (3.6) se obtine expresia campului magnetic.
III 3.1.1. Tensiunea magnetica produsa de infasurari
monofazate repartizate
Cea mai
simpla infasurare monofazata care determina p perechi de poli este formata din
p bobine inseriate. Pentru simplificarea prezentarii, in figura 3.5 a si in
figura 3.9 a s-a prezentat cazul unei infasurari care determina p=2 perechi de
poli magnetici. Infasurarea este formata din p bobine inseriate, asezate la ![]() distanta una de
cealalta (vezi paragraful II 2) si
parcurse de curentul i. Numarul de spire al infasurarii este
distanta una de
cealalta (vezi paragraful II 2) si
parcurse de curentul i. Numarul de spire al infasurarii este
![]() :
:
![]() (3.7)
(3.7)
Aplicand legea circuitului magnetic pe curba ![]() (A B D C A), care se
inchide numai prin zona polului sud (vezi figura 3.9.b), se obtine
(vezi
egalitatile
(3.5.b)
(A B D C A), care se
inchide numai prin zona polului sud (vezi figura 3.9.b), se obtine
(vezi
egalitatile
(3.5.b)

respectiv
![]() sau
sau ![]() (3.8 a)
(3.8 a)
unde ![]() si
si ![]() sunt tensiunile
magnetice corespunzatoare zonelor (AB) si (CD) de pe curba
sunt tensiunile
magnetice corespunzatoare zonelor (AB) si (CD) de pe curba ![]() . Din ecuatia (3.8 a) rezulta ca tensiunea magnetica a
intrefierului sub polul sud este constanta si egala cu
. Din ecuatia (3.8 a) rezulta ca tensiunea magnetica a
intrefierului sub polul sud este constanta si egala cu ![]() .
.

Similar, se demonstreaza ca tensiunea magnetica a
intrefierului sub polul nord este constanta si egala cu ![]() .
.
Astfel curba de variatie a tensiunii magnetice din
intrefier ![]() , produsa de catre infasurarea considerata, are expresia:
, produsa de catre infasurarea considerata, are expresia:
 (3.8 b)
(3.8 b)
Aceasta curba este o functie para, periodica cu perioada ![]() si este reprezentata
in figura 3.9.c. In expresia (3.8.b)
si este reprezentata
in figura 3.9.c. In expresia (3.8.b) ![]() este deschiderea
unghiulara a bobinei:
este deschiderea
unghiulara a bobinei:
![]()
unde ![]() este pasul polar (vezi relatia de definitie
este pasul polar (vezi relatia de definitie
Dependenta dintre tensiunile magnetice
![]() si
si ![]() se obtine prin
aplicarea legii circuitului magnetic pe curba
se obtine prin
aplicarea legii circuitului magnetic pe curba ![]() (
(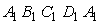 ) (vezi figura
3.9.b):
) (vezi figura
3.9.b):
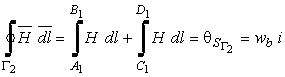
respectiv
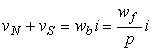 (3.8.c)
(3.8.c)
Folosind dependenta (3.8.c), tensiunea
magnetica din intrefier ![]() , definita de relatia (3.8.b), se poate descompune in
serie armonica:
, definita de relatia (3.8.b), se poate descompune in
serie armonica:
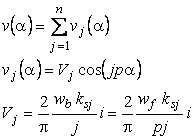 (3.9)
(3.9)
unde ![]() este ordinul armonicii spatiale,
iar
este ordinul armonicii spatiale,
iar ![]() este amplitudinea armonicii spatiale de ordin j si se calculeaza cu relatia
este amplitudinea armonicii spatiale de ordin j si se calculeaza cu relatia
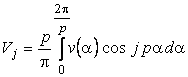 (3.9.a)
(3.9.a)
rezultata din expresia coeficientilor seriei.
Factorul ![]() , numit coeficient de scurtare al infasurarii
pentru armonica spatiala j, are expresia:
, numit coeficient de scurtare al infasurarii
pentru armonica spatiala j, are expresia:
![]() (3.10)
(3.10)
si
depinde, prin intermediul deschiderii
raportate ![]() , de constructia bobinei.
, de constructia bobinei.
De remarcat
ca valoarea raportului ![]() influenteaza valoarea
amplitudinii armonicii spatiale de ordin j (vezi expresia
influenteaza valoarea
amplitudinii armonicii spatiale de ordin j (vezi expresia
Prin definitie, armonica spatiala a tensiunii magnetice care are in intrefier acelasi numar de alternante cu tensiunea magnetica a intrefierului se numeste armonica fundamentala.
Pentru cazul considerat, armonica fundamentala are ordinul j=1
In figura 3.9.d s-au reprezentat armonica fundamentala si armonica a doua spatiala (j=2). Pentru claritate, reprezentarea s-a facut la alta scara decat scara utilizata in figura 3.9.c.
Pentru a ilustra importanta valorii
deschiderii y a bobinei asupra
amplitudinii armonicilor spatiale ale tensiunii magnetice, in tabelul 3.1 s-au
prezentat valorile raportului (![]() ) pentru primele 5 armonici spatiale, in functie de valori
ale deschiderii raportate
) pentru primele 5 armonici spatiale, in functie de valori
ale deschiderii raportate ![]() .
.
Tabelul 3.1.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Din expresia factorului de scurtare
(3.10), rezulta ca acesta are, in modul, aceleasi valori pentru aceeasi scurtare
raportata ![]() :
:
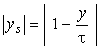
pentru ca
![]()
indiferent
daca ![]() sau
sau ![]() . Se prefera
scurtarea pasului (
. Se prefera
scurtarea pasului (![]() ), pentru a
obtine o economie de material prin scurtarea capului de bobina.
), pentru a
obtine o economie de material prin scurtarea capului de bobina.
Pe baza rezultatelor prezentate in tabelul 3.1 se pot obtine concluzii importante.
|
Analiza influentei deschiderii y a bobinei asupra valorii amplitudinii armonicilor spatiale ale tensiunii magnetice arata: vezi relatia 3.9.a)), ceea ce conduce la o reducere si mai rapida a amplitudinii armonicilor superioare spatiale. vezi valoarea coeficientului |
In multe cazuri practice pentru reducerea amplitudinii armonicilor spatiale se utilizeaza si alte elemente constructive, in afara scurtarii pasului: repartizarea bobinelor si inclinarea laturilor de bobina
Coeficientul
de infasurare ![]() considera atat
influenta scurtarii fiecarei bobine elementare, cat si influenta repartizarii
celor
considera atat
influenta scurtarii fiecarei bobine elementare, cat si influenta repartizarii
celor ![]() spire pe bobinele
elementare. Se observa ca, in cazul
general, cele doua influente, scurtarea si repartizarea, nu se pot separa vezi expresia (3.11.b)).
spire pe bobinele
elementare. Se observa ca, in cazul
general, cele doua influente, scurtarea si repartizarea, nu se pot separa vezi expresia (3.11.b)).
Observatii
Numai in cazul particular al unei bobine divizate in q bobine elementare identice, asezate in crestaturi consecutive, se poate face o separatie intre efectul repartizarii si efectul scurtarii
Pentru acest caz particular factorul de
infasurare ![]() , corespunzator armonicii spatiale
, corespunzator armonicii spatiale
![]() , este un produs:
, este un produs:
![]() (3.12)
(3.12)
unde ![]() este coeficientul de
repartizare:
este coeficientul de
repartizare:
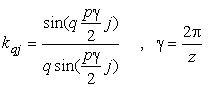 (3.12 a)
(3.12 a)
iar ![]() reprezinta unghiul
geometric la centru intre doua crestaturi succesive.
reprezinta unghiul
geometric la centru intre doua crestaturi succesive.
Coeficientul de repartizare ![]() este totdeauna
subunitar.
este totdeauna
subunitar.
Daca se alege ca axa spatiala axa magnetica a celor q bobine, atunci expresia (3.11) a tensiunii magnetice devine:
 (3.13)
(3.13)
Pentru a ilustra
influenta repartizarii unei bobine asupra amplitudinii armonicilor spatiale ale
tensiunii magnetice, in tabelul 3.2 sunt prezentate valorile raportului ![]() calculate cu (3.12.a)
in ipoteza unor infasurari care conserva valoarea produsului (
calculate cu (3.12.a)
in ipoteza unor infasurari care conserva valoarea produsului (![]() ), iar toate bobinele elementare au pas diametral. Raportul
), iar toate bobinele elementare au pas diametral. Raportul ![]() influenteaza direct
valoarea amplitudinii armonicii spatiale de ordin j (vezi expresiile sau
influenteaza direct
valoarea amplitudinii armonicii spatiale de ordin j (vezi expresiile sau
Tabelul 3.2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pe baza rezultatelor prezentate in tabelul 2.2 se pot obtine concluzii importante privind efectul repartizarii bobinei.
|
Efectele divizarii unei infasurari asupra valorii amplitudinii armonicilor spatiale sunt: In multe cazuri
practice, in special la masinile de mica putere, bobina nu se aseaza cu
laturile paralele cu generatoarea armaturii (vezi figura 2.6.a), ci se aseaza inclinat (vezi figura 3.10.b); unde s-a considerat ca inclinarea poate
fi descrisa de unghiul 2 Se
demonstreaza ca amplitudinea armonicii spatiale de ordin j a tensiunii
magnetice generate in intrefier de catre o infasurare cu laturile de bobina
inseriate este afectata de coeficientul subunitar
unde D este diametrul armaturii. In cazurile practice inclinarea t a bobinei nu depaseste marimea unui pas de crestatura
Pentru a ilustra efectul inclinarii, in tabelul 3.3 sunt prezentate valorile factorului de inclinare pentru diverse armonici spatiale, considerand inclinarea cu un pas de crestatura; s-a analizat cazul a doua armaturi cu numere diferite de crestaturi: o armatura are Z=18, iar cealalta Z=36 crestaturi. Tabelul 3.3
S-au prezentat valorile obtinute pentru primele patru armonici impare si pentru primele doua armonici de dantura de ordin: Pe baza rezultatelor prezentate in tabelul 3.3 se pot obtine concluzii importante legate de efectul inclinarii laturilor de bobina.
|