Caracteristici BODE

Caracteristici BODE

  Daca u(t) este un semnal sinusoidal atunci in regim permanent sinusoidal si y(t) este un semnal sinusoidal. El va avea alta amplitudine si alta faza.

Aceasta inseamna ca:

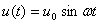atunci

Se constata experimental ca relatia dintre y₀ si x₀ depinde de configuratia sistemului si de va 959h79j loarea lui . De asemenea valoarea lui depinde de configuratia sistemului si de valoarea lui

Pe baza acestor observatii s-au introdus caracteristicile de pulsatie numite in mod curent caracteristici de frecventa. Astfel se definesc caracteristicile:

(1) numita caracteristica de amplitudine si

(2) numita caracteristica de faza.

Dependenta lui si de ω este o trasatura generala a sistemelor. Expresiile lui f₁ si f₂ sunt specifice fiecarui sistem in parte. Din considerente practice inclusiv de reprezentare grafica se lucreaza cu alte caracterisitici care provin din f₁ si f₂. Ele au ca variabila logaritmul zecimal al lui ω.

Vom nota (3)

Axa absciselor este numita axa logaritmica (este impartita dupa valoarea logaritmului dar notata cu cantitatile logaritmate).

O decada 1dec este intervalul in care valoarea lui ω creste de 10 ori.

ω = 2πf

Daca x > 0 atunci 20lg(x) se numeste aproximarea lui x in decibeli x_dB

x = 10 x_dB = 20 dB

x = 2 x_dB = 6dB

x = 0,5 x_dB = 20 lg(1/2) = - 6 dB

Caracteristicile BODE reprezinta caracteristicile care inlocuiesc pe f₁ si f₂ astfel:

F₁(ω_lg) = 20 lg f₁(ω) = |f₁|_dB    (4)

Expresia lui f₁ in dB considerata in functie de lg ω se numeste caracteristica amplitudine pulsatie.

A doua caracteristica numita caracteristica faza-pulsatie este F₂(ω_lg)= f₂(ω) (5)

adica considerarea fazei.

F₁ si F₂ se numesc caracterisitici BODE sau caracteristici logaritmice de pulsatie sau de frecventa.

Importanta caracteristicilor BODE consta in faptul ca ele reperzinta un model al sistemului, iar acest lucru rezulta dintr-un studiu care arata ca cele doua caracteristici pot sa fie obtinute cu ajutorul particularizarii functiei de transfer a sistemelor pe ramura pozitiva a axei imaginare astfel presupunem ca sistemul are functia de transfer H(s) adica H este definita pe tot planul "s".

Se numeste functie raspuns la pulsatie H(j ω) = H(s)| _s=jω (6)

H(j ω) este un numar complex in reprezentare polara, astfel putem scrie:

(7)

Se demonstreaza ca in regim permanent sinusoidal semnalului de intrare u(t) = u₀sin ωt ii corespunde la iesire semnalul y(t) = u₀|H(j ω)|·sin (ωt+argH(j ω))

(8)

Ca urmare caracteristicile BODE pot fi scrise si sub forma:

F₁(ω_lg) = |H(j ω)|_dB = |H|_dB (9)

F₂(ω_lg) = arg H(j ω) = φ_H (10)

pentru ω>0

Formulele (1), (2), (9) si (10) sunt foarte importante fiindca potrivit primelor formule caracteristicile BODE pot fi determinate experimental asa cum au fost definite, iar potrivit ultimelor formule acestea pot fi calculate analitic. In consecinta rezultatele obtinute pe cale analitica pot sa fie aplicate unor caracteristici obtinute experimental.

Exemple:

1. Un sistem electric - un circuit RC

uy

2. Un sistem mecanic - un sistem resort-amortizor

- sistem de ordinul I

m

- system de ordinul I

Forma generala a unui system de ordinul I este:

(11)

Functia de transfer a unui sistem de ordinul I va fi:

Un numar complex x+jy poate fi scris:

Astfel modulul va fi:

si defazajul va fi:

zona

zona

zona

pulsatiilor joase

pulsatiilor medii

pulsatiilor inalte

Zona pulsatiilor medii caracterizeaza comportarea sistemului in regimul tranzitoriu propriu-zis.