Circuite liniare de curent continuu

Circuite liniare de curent continuu

Aceste circuitele se compun din surse de curent continuu si din rezistoare, legate intre ele prin conductoare a caror rezistenta foarte mica se neglijeaza. Exceptie fac problemele transportului de energie in curent continuu unde, datorita lungimii relativ mari, rezistenta conductoarelor de legatura trebuie luata in calculul caderilor de tensiune (v. 8.3.2.).

Studiul circuitelor de curent continuu se face pe baza legilor electrocineticii ale caror consecinte sunt reflectate in teoremele care vor fi prezentate in cadrul metodelor de rezolvare ale acestor circuite. Rezolvarea consta in a se determina intensitatile curentilor din laturi cand se cunosc caracteristicile ale surselor si rezistentele ale receptoarelor.

8.3.1. Circuitul simplu de curent continuu

Circuitul simplu (fig. 8.38) cuprinde o singura sursa de tensiune electromotoare si rezistenta interna , debitand pe un rezistor de rezistenta . Conductoarele de legatura se considera filiforme si de rezistenta neglijabila. Se reaminteste ca prin conductor filiform se intelege conductorul a carui sectiune are dimensiuni mici in raport cu lungimea, ceea ce permite sa se aprecieze ca densitatea curentului electric de conductie este uniform repartizata in sectiune si ca vectorul densitate de curent este tangent la axa conductorului in oricare punct al sectiunii.

Calculul intensitatii curentului

Relatia de calcul a intensitatii curentului este furnizata de legea conductiei: . Tensiunea de-a lungul firului, datorata campului coulombian generat de acumularea pe electrozii sursei de curent a sarcinilor este nula pentru conturul inchis , descris de circuit, asa ca vom avea:

si deci , (8.44)

in care este rezistenta totala a circuitului. Produs 838h79i ele de forma sau se numesc caderi de tensiune.

Din punctul de vedere practic, intereseaza valoarea intensitatii curentului prin receptorul de rezistenta R sau prin conductoarele de legatura si care este comod a fi exprimata in functie de tensiunea aplicata la bornele receptorului sau circuitului, potrivit formularii a legii conductiei, cu atat mai mult cu cat, spre deosebire de tensiunea electromotoare, tensiunea se masoara usor cu voltmetrul.

Tensiunea la bornele sursei, aici egala cu tensiunea aplicata la bornele receptorului, este o marime care intervine in mod obisnuit in calculul circuitelor.

La scrierea relatiilor intre marimile de circuit, este necesara -dupa cum s-a aratat- asocierea sensurilor pentru diferitele marimi electrice in acelasi mod in care s-a facut aceasta asociere la enuntarea legilor. Acolo unde sensurile de referinta a doua marimi sunt independente intre ele, trebuie sa se prezinte in mod explicit conventia folosita pentru scrierea relatiilor dintre aceste marimi.

Prin atribuirea sensului de referinta al tensiunii la borne pentru circuitul din figura 8.38, de la A la B, este satisfacuta atat regula de la generator cat si regula de la receptor. Astfel, in functie de sensul de referinta al curentului, pentru ramura sursei, cuprinsa intre cele doua borne, se va scrie:

,

iar pentru ramura receptorului:

Din prima ecuatie se deduce:

de unde se vede ca tensiunea electromotoare a sursei este egala tensiunea la borne cu la mersul in gol () precum si semnificatia de "cadere de tensiune" a produsului .

Bilantul puterilor si energiilor. Transferul maxim de putere

Ecuatia de tensiune (8.47), inmultita in ambii membri cu intensitatea curentului, devine ecuatia bilantului de puteri:

in care: este puterea produsa de sursa (puterea generata - ), este pierderea de putere in sursa, iar este puterea debitata - .

Daca se neglijeaza rezistenta conductoarelor de legatura, puterea debitata de sursa rezulta egala cu aceea consumata de receptor:

.

Randamentul circuitului simplu este, prin definitie, . Inlocuindu-se puterile cu expresiile lor, rezulta:

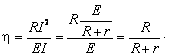
Randamentul va fi maxim atunci cand puterea debitata va fi maxima si se realizeaza cu conditia , de unde rezulta:

,

adica rezistenta circuitului exterior sursei sa fie egala cu rezistenta ei interna. Valoarea maxima a randamentului transformarii energiei chimice in energie electrica este, prin urmare, de 50%.

In intervalul de timp de la 0 la t, ecuatia de bilant energetic al circuitului simplu va fi:

unde este energia generata, - energia pierduta prin efect Joule in rezistenta sursei, iar este energia debitata, egala in cazul de fata cu aceea consumata de receptor: .

8.3.2.Transportul energiei in curent continuu

Atunci cand energia este transportata de la sursa la receptor printr-o linie formata dintr-un conductor de ducere si unul de intoarcere, avand lungimea (fig. 8.39) si rezistenta neneglijabila, are loc o cadere de tensiune si o pierdere de putere in linia de transmisie.

Daca tensiunea la capatul liniei este , curentul in linie are valoarea , unde este rezistenta liniei iar , rezistenta receptorului.

Datorita caderii de tensiune pe linia de lungime , exprimata prin relatia:

,

tensiunea la bornele receptorului va fi: . La o valoare mare a caderii de tensiune pe linie, tensiunea la bornele receptorului poate fi insuficienta pentru functionarea normala. De aceea, sectiunea conductoarelor de legatura trebuie aleasa astfel incat caderea de tensiune pe linie sa fie cel mult egala cu caderea de tensiune maxima admisa de receptor: .

Sectiunea necesara se va determina cu ajutorul relatiei:

(8.54)

unde este curentul nominal al receptorului inscris pe placa indicatoare sau calculat fie in functie de tensiunea nominala si de rezistenta receptorului, fie in functie de tensiunea si puterea nominala:

(8.55)

Conductorul ales trebuie sa corespunda si din puncul de vedere al incalzirii maxime admise. La 'trecerea' curentului prin conductor are loc incalzirea acestuia prin efect Joule, care corespunde unei pierderi de putere in linie:. Pentru ca temperatura conductorului sa nu depaseasca anumite limite, dincolo de care nu mai este garantata integritatea izolatiei liniei, se verifica daca intensitatea a curentului pe linie nu este mai mare decat intensitatea maxima admisa in conductorul ales.

Puterea transmisa de sursa fiind:

(8.56)

rezulta ca, datorita pierderilor de putere in linie, la receptor va ajunge puterea:

, (8.57)

iar randamentul transmisiei (liniei) care primeste la intrare puterea si cedeaza la iesire puterea va fi:

(8.58)

Randamentul unei linii trebuie sa fie de circa 95%. Punand conditia , rezulta un nou criteriu de dimensionare al acesteia, plecand de la relatia pierderilor:

, (8.59)

de unde, tinandu-se seama ca , rezulta ca sectiunea necesara este:

(8.60)

Sectiunea conductorului ales pe acest criteriu se verifica la cadere de tensiune ca mai sus.

8.3.3. Calculul circuitelor de curent continuu

Circuitele sau retelele electrice de curent continuu, sunt circuite ramificate continand L laturi si N noduri. Latura este portiunea neramificata de circuit formata din rezistoare (latura pasiva), rezistoare si surse (latura activa) sau numai surse de tensiune electromotoare. Nodul este punctul de ramificatie in care se intalnesc cel putin trei laturi. Succesiunea de laturi care formeaza un contur inchis se numeste ochi de retea. Se demonstreaza ca o retea avand N noduri si L laturi este constituita din L-N+1 ochiuri independente (al caror contur nu se obtine prin combinatii ale contururilor altor ochiuri).

Analiza retelelor de c.c. se bazeaza pe legea lui Ohm, legea conservarii sarcinii electrice si pe teoreme, consecinte ale legilor, care vor fi expuse in continuare.

Metoda reducerii

Metoda este aplicata retelelor care grupeaza sursele separat de receptoare, ca in figura 8.40 si reduce -practic- calculul circuitului electric la calculul circuitului simplu.

Daca se inlocuiesc receptoarele printr-unul echivalent, de rezistenta , in conformitate cu teoremele rezistentelor echivalente, iar sursele cu una echivalenta, avand tensiunea electromotoare si rezistenta interna , se reduce circuitul la unul simplu, ca in figura 8.41.

Teoremele rezistentelor echivalente arata ca:

- rezistenta echivalenta a n rezistoare in serie este data de relatia:

;

rezistoare in paralel este data de relatia:

Tensiunea electromotoare echivalenta si rezistenta echivalenta a surselor in serie rezulta din aplicarea legii lui Ohm portiunii de circuit din figura 8.42. Se obtine relatia:

.

Inlocuindu-se cele n surse printr-una singura, se va scrie:

si prin identificarea relatiilor (8.63) si (8.64), membru cu membru, rezulta:

si

Pentru sursele in paralel, care au aceeasi tensiune la borne (fig. 8.43.), se scrie legea lui Ohm pentru fiecare latura:

,

,

iar pentru sursa echivalenta se scrie, analog:

, (8.68)

unde:

. (8.69)

Explicitand curentii din ecuatiile (8.67) si (8.68) si inlocuindu-i in ecuatia (8.69) se obtine, prin identificara membrului stang cu membrul drept:

(8.70)

si

(8.71)

Revenind la reteaua din figura 8.40, se va obtine, succesiv:

,

si , , ,

si , ^,

unde si sunt rezistentele echivalente ale rezistoarelor in paralel, al caror indice urmeaza dupa 'ep'.

In continuare, fiind cunoscuta tensiunea la bornele sursei, , se pot determina curentii prin ramurile sale cu ajutorul relatiilor (8.64) la (8.66).

Metoda superpozitiei

Aceasta metoda poate simplifica calculul retelelor electrice in care lucreaza mai multe surse de energie electrica. Ea se bazeaza pe principiul suprapunerii efectelor enuntat de Helmoltz, potrivit caruia, din suprapunerea mai multor stari de echilibru rezulta tot o stare de echilibru.

Potrivit acestui principiu, curentul intr-o latura oarecare a circuitului va rezulta ca suma algebrica a curentilor produsi in acea latura de fiecare tensiune electromotoare in parte. In consecinta, se determina curentii produsi de fiecare sursa in latura de circuit respectiva, presupunand ca sursa lucreaza singura in retea, si se insumeaza apoi curentii partiali, tinandu-se seama de sensul lor.

Atunci cand se calculeaza curentii, se au in vedere rezistentele interioare ale tuturor surselor de circuit. Cu alte cuvinte, se pasivizeaza laturile circuitului in afara de una singura.

Pentru exemplificare, se aplica metoda superpozitiei pentru circuitul din figura 8.44a. Se presupune, mai intai, ca in circuit actioneaza numai sursa , ca in figura 8.44b.

Notandu-se rezistentele laturilor 1 si 2 cu si , curentii produsi in retea de sursa vor fi:

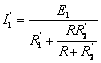^, si

Se calculeaza, in continuare, curentii produsi in retea de sursa cand sursa este pasivizata (fig. 8.44c):

^, si

Curentii reali prin laturi vor rezulta prin suprapunerea celor calculati mai sus, tinandu-se seama de sensurile curentilor din cele trei scheme:

, si .

Metoda teoremelor lui Kirchhoff

Metoda fiind cunoscuta inca de la fizica de liceu, se va reaminti aici numai metodologia utilizarii ei.

Aplicarea teoremei I a lui Kirchhoff (consecinta a legii conservarii sarcinii electrice), cu referire la nodurile retelei, conduce la N-1 ecuatii independente, iar aplicarea teoremei a II-a, cu referire la conturul ochiurilor independente (consecinta a legii conductiei electrice), conduce la alte L-N+1 ecuatii. Se obtine un sistem de L ecuatii, necesar si suficient pentru determinarea celor curenti din laturi.

Scrierea ecuatiilor trebuie sa se faca cu respectarea regulilor de asociere a sensurilor de referinta si comportaa urmatoarele etape:

- se atribuie curentului din fiecare latura un sens arbitrar, notat cu o sageata;

- se scriu ecuatiile teoremei I pentru N-1 noduri, considerand pozitivi curentii care ies din nod si negativi pe aceia care intra:

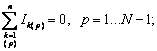
- se alege un sens arbitrar de parcurgere a fiecarui ochi independent, notat cu o sageata ronda, si se scrie ecuatia teoremei a II-a pentru fiecare:

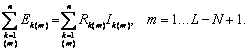
In aceaste ecuatii sunt pozitive tensiunile electromotoare orientate in sensul de parcurgere al ochiului si caderile de tensiune corespunzatoare curentilor care se asociaza tot cu sensul de parcurgere;

- solutiile sistemului liniar format cu cele L ecuatii (8.72) si (8.73), sunt intensitatile curentilor din laturi. Daca unele rezulta cu valori negative, sensul curentilor respectivi este invers fata de acela presupus initial.

Metoda tensiunii intre noduri

Daca reteaua are doua noduri, ca in figura 8.45, curentii din laturile sale pot fi determinati printr-o metoda mai simpla si mai rapida decat prin rezolvarea ecuatiilor obtinute prin aplicarea teoremelor lui Kirchhoff.

Se adopta ca sens de referinta pentru curentii si pentru tensiunile electromotoare sensul de la nodul B catre nodul A si se noteaza potentialele nodurilor cu si . Tensiunea intre cele doua noduri este: .

Scriindu-se ecuatia legii lui Ohm fiecare latura, se obtine expresia intensitatii curentului din latura respectiva sub forma:

(8.74)

Teorema I a lui Kirchhoff aplicata nodului A conduce la relatia:

de unde rezulta expresia tensiunii dintre noduri:

(8.75)

In rezistenta a unei laturi se include si rezistenta a sursei respective, iar tensiunile electromotoare orientate de la nodul A catre nodul B vor apare in relatia (8.75) cu semnul minus.

Cunoscandu-se tensiunea intre noduri calculata astfel, se poate calcula intensitatea fiecaruia dintre curenti cu ajutorul relatiilor (8.74). Daca din calcule rezulta valori negative de curenti, inseamna ca sensul lor real nu se asociaza cu sensul de referinta ales.

Metoda circuitelor independente

Aceasta metoda, numita si metoda buclelor sau metoda curentilor de ochiuri a lui Maxwell, permite determinarea intensitatii curentilor din retelele electrice, cu ajutorul unui numar redus de ecuatii fata de acela ce rezulta din aplicarea teoremelor lui Kirchhoff.

In metoda circuitelor independente se considera reteaua ca o suprapunere de circuite simple, separate, asa cum s-a reprezentat punctat in figura 8.46.

Se presupune ca fiecare din aceste circuite sunt parcurse de curenti proprii, notati cu . Ei se numesc curenti simpli, curenti de bucla sau curenti ciclici. Sensul curentilor de bucla este ales arbitrar si notat cu o sageata ronda.

Pentru fiecare bucla in parte se scrie teorema a II-a a lui Kirchhoff, tinandu-se cont de urmatoarele:

- tensiunile electromotoare ale surselor care debiteaza in sens invers celui arbitrar ales pentru curentul din bucla, se iau cu semnul minus;

- in rezistentele unei bucle, dau caderi de tensiune si curentii ciclici din buclele adiacente. Aceste caderi de tensiune se iau cu semnul minus atunci cand curentii care le produc sunt de sens contrar celui in care se parcurge bucla la care se face referirea.

Tinandu-se cont si de rezistentele surselor, care in figura 8.46 se considera inglobate in rezistenta totala a laturilor, se obtine un sistem de ecuatii, in numar egal cu acela care rezulta din aplicarea teoremei a II-a a lui Kirchhoff in retea:

,

,

,

in care reprezinta suma rezistentelor din bucla , iar reprezinta rezistenta laturii comune a circuitelor simple si . Cu s-a notat suma tensiunilor electromotoare din circuitul simplu .

Curentii reali din laturile retelei se obtin prin suprapunerea curentilor din circuitele simple care contin latura respectiva.

Sub forma matriceala, sistemul ecuatiilor (8.76) se scrie:

.

Sistemele de ecuatii de tipul (8.77) se rezolva imediat cu ajutorul unui subprogram din biblioteca MATLAB.

Metoda potentialelor la noduri

Se considera o retea electrica si o latura a acesteia, cuprinsa intre nodurile si (fig. 8.47). Ecuatia legii lui Ohm, scrisa pentru fiecare asemenea latura, va conduce la ecuatii de tipul:

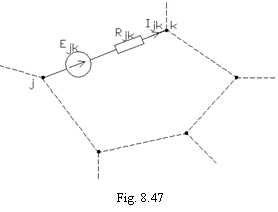
din care rezulta intesitatile curentilor cu expresii:

sau:

.

Curentii din laturi vor fi astfel determinati daca se vor cunoaste potentialele nodurilor retelei.

Daca se considera potentialul nodului oarecare drept potential de referinta () si se vor scrie ecuatiile teoremei I a lui Kirchhoff la toate nodurile, cu exceptia nodului , folosind pentru curenti expresiile (8.78) se obtin N-1 ecuatii de forma:

, (8.79)

in care: este potentialul nodului ; este suma conductantelor laturilor conectate in nodul ; este suma produselor dintre conductantele laturilor din nodul si potentialele nodurilorde la celalalt capat al laturii; sunt tensiunile electromotoare ale surselor din laturile ce converg in nodul . Produsele sunt pozitive cand tensiunea electromotoare din latura este orientata catre nodul j.

Notandu-se si , unde este curentul de scurtcircuit al laturii , rezulta sistemul ecuatiilor metodei sub forma:

(8.80)

unde conductantele sunt pozitive iar sunt negative.

Sistemul ecuatiilor (8.80), scris sub forma:

, (8.81)

se rezolva rapid cu ajutorul subprogramelor aflate in biblioteca MATLAB.

Metodele generatoarelor echivalente

Aceste metode sunt utile pentru simplificarile care se pot obtine in calcule, atunci cand intereseaza, de fapt, intensitatea curentului intr-o singura latura a unei retele.

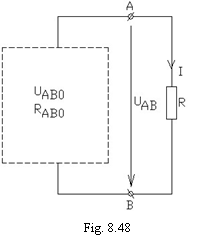Metoda generatorului echivalent de tensiune (Th venin-Helmholtz) presupune o retea pentru care se cere numai intensitatea curentului prin latura ce contine rezistorul din figura 8.48 (restul retelei este sugerat prin chenarul punctat).

Pentru rezistorul , restul retelei este echivalent cu un generator ale carui borne sunt A si B.

Tensiunea electromotoare a generatorului echivalent este egala cu tensiunea la bornele A, B cand rezistorul este deconectat, iar rezistenta sa interna, , se calculeaza, considerand sursele pasivizate, cu ajutorul teoremelor rezistentelor echivalente. Fiind cunoscute aceste marimi se obtine:

(8.82)

Ecuatia (8.82) reprezinta teorema Th venin-Helmholtz , conform careia curentul I debitat de reteaua liniara pe rezistorul R este egal cu raportul dintre tensiunea de mers in gol la bornele A, B si suma dintre rezistenta exterioara R si rezistenta echivalenta a retelei pasivizate, vazuta prin aceleasi borne (cu rezistorul R deconectat).

Metoda generatorului echivalent de curent (Norton), considera aceeasi retea din figura 8.48 si utilizeaza teorema Norton, conform careia tensiunea U produsa in sarcina de reteaua liniara activa care alimenteaza rezistenta exterioara R este egala cu raportul dintre curentul de scurtcircuit al retelei si suma dintre conductanta interioara a retelei pasivizate si conductanta exterioara.

Din ecuatia (8.82) se obtine:

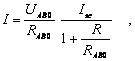
unde:

(8.84) ^,

este curentul de scurtcircuit al generatorului echivalent cu reteaua .

Introducandu-se conductantele si tinand cont de expresia (8.84), relatia (8.83) devine:

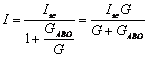sau

si exprima teorema lui Norton.

Curentul de scurtcircuit al sursei se calculeaza considerand nodurile A si B ale retelei din figura 8.48 ca fiind in contact galvanic (rezistenta R deconectata iar bornele scurcircuitate cu un conductor de rezistenta neglijabila).