Circuite liniare in regim electrocinetic nestationar oarecare
Regimul electrocinetic numit aici nestationar oarecare este regimul variabil in care intensitatile curentilor, tensiunile, potentialele electrice etc sunt functii oarecare de timp. El se supune legilor electrocineticii, prezentate in capitolul 4: legea conservarii sarcinii, legea transformarii energiei prin curentul electric de conductie (Joule - Lenz), legea conductiei electrice (Ohm), legi a caror valabilitate nu este restransa la nici un regim de variatie in timp a fenomenelor.
8.4.1. Ecuatiile circuitelor electrice in regim variabil
Caracterizarea locala a regimului
electrocinetic se face cu ajutorul legii lui Ohm 
in care, intensitatea campului electric 
poate avea o componenta de tip coulumbian -
si
una de tip rotational
- 
produsa prin inductie electromagnetica. Sub o
forma
mai desfasurata,
legea se scrie:
.
Sub forma globala, cu referire la o portiune neramificata de conductor, legea are forma:
,
in care 
este tensiunea de-a lungul firului, 
este t.e.m. indusa iar 
este tensiunea electromotoare provenita din
campuri electrice imprimate.
O portiune neramificata de circuit poate contine
rezistoare, bobine, capacitati. Diversii parametrii, considerati concentrati,
se admit ca fiind sediul unei singure forme de transformare a energiei. Daca
asupra unui circuit electric exercita o actiune electromagnetica alt circuit din exterior, atunci la
parametrii concentrati se adauga si inductivitatea mutuala 
.
Exemplele urmatoare
vor fi edificatoare pentru modul in care se scriu ecuatiile
circuitelor intr-un asemenea regim in care, spre deosebire de cele din
subcapitolul 8.3, campul electric nu mai este irotational:
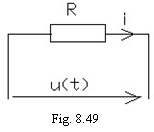
i) pentru circuitul simplu cu rezistor, caruia i se
aplica la borne o tensiune variabila in timp 
(fig. 8.49), ecuatia
(8.87) va fi:
. (8.88)
de unde rezulta:
(8.89)
Curentul are deci aceeasi forma de variatie in timp ca si tensiunea aplicata la borne;
ii) ecuatia
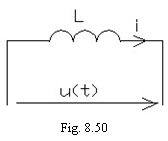
(8.87) pentru bobina ideala -cu rezistenta neglijabila-
(fig. 8.50), alimentata cu tensiunea 
se scrie:
(8.90)
unde este t.e.m. autoindusa:
(8.91)
si
prin urmare (considerandu-se 
=const. in
timp) :
adica:
(8.92)
si
(8.93)
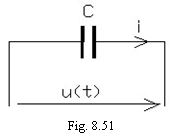iii) circuitul simplu cu condensator din figura 8.51 are ecuatia:
(8.94)
de unde:
(8.95)
(8.96)
si (considerandu-se
=const. in
timp):
(8.97)
iu) ecuatia portiunii neramificate de circuit care contine mai multi parametrii (fig. 8.52) va fi:
(8.98)
unde este t.e.m. imprimata, 
este t.e.m. autoindusa, iar 
este t.e.m. de inductie mutuala (considerandu-se
constant in timp).
Tinandu-se seama de relatia (8.97) ecuatia (8.98) se scrie:
Pentru circuitul inchis al unei bucle dintr-o retea complexa (
) ecuatia
(8.99), exprimand
teorema a II-a a lui Khirchhoff, va fi:
unde 
este suma t.e.m. a surselor (inclusiv a t.e.m.
produse prin inductie mutuala).
Tensiunea electromotoare de inductie mutuala se va introduce in membrul I
al ecuatiei (8.100) cu semnul plus ( 
) daca
curentii 
si 
sunt ambii in sensul de parcurgere al buclei
si cu semnul minus (
) daca
ambii sunt in sens invers fata de acela in care se parcurge bucla. Daca cei doi
curenti au sensuri diferite, semnul este minus
atunci cand curentul este in sensul de parcurgere al buclei si plus in caz contrar.
8.4.2. Energetica circuitelor electrice in regim variabil
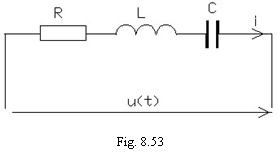
Se considera circuitul din figura 8.53 a carui ecuatie este:
Inmultindu-se ambii termeni ai ecuatiei (8.101) cu 
se obtine ecuatia de bilant energetic pentru
intervalul de timp 
:
In intervalul de timp de la 0 la 
in care intensitatea curentului creste de la 0
la iar sarcina pe armaturile condensatorului de
la 0 la 
, energia
intrata in circuit se transforma o parte in caldura
in rezistenta
circuitului, iar cealalta parte se acumuleaza in campul
magnetic al bobinei si in campul electric al
condensatorului:
adica:
Energiile inmagazinate in campul magnetic al bobinei si
in campul electric al condensatorului, reprezentate de ultimii doi termeni, se
restituie circuitului in acele intervale de timp in care curentul este in
scadere. Intr-adevar, in intervalul de timp de la 0 la 
in care intensitatea curentului scade de la la 0, iar sarcina condensatorului de la la 0 ecuatia de bilant
este:
adica:
sau:
(8.107)
Prin urmare, energia furnizata de sursa, energia inmagazinata in campul magnetic al bobinei si aceea inmagazinata in campul electric al condensatorului se transforma, in acest interval de timp, in caldura in rezistenta circuitului. Prin 'inmagazinata in campul ' se intelege ca energia aste rezidenta in materialul in care se produce campul (magnetic si electric).
8.4.3. Metode operationale de rezolvare a circuitelor in regim variabil
Metoda directa de studiu a regimului variabil este laborioasa si practic ineficienta in cazul circuitelor cu structura complicata. Pentru acestea devin practice metodele care transforma ecuatiile integro-diferentiale ale circuitelor in ecuatii algebrice cu ajutorul operatorilor liniari care asociaza functiilor de timp o anumita imagine.
Metoda transformatei Laplace
Calculul se sistematizeaza scriind direct ecuatiile teoremelor lui Kirchhoff sub forma operationala, care exprima relatiile dintre imaginile curentilor si tensiunilor.
La forma operationala a teoremelor lui Kirchhoff se ajunge cu ajutorul teoremelor cunoscute ale transformarii Laplace (v. cap. 9):
. (8.108)
Imaginile functiilor de timp din (8.108) sunt:
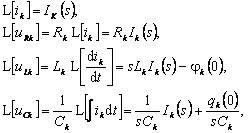
unde: 
este valoarea initiala a sarcinii
condensatorului si 
este valoarea initiala a fluxului bobinei din
latura 
.
Marimile:
si 
,
se numesc impedante
operationale proprii, 
se numeste impedanta operationala mutuala
dintre laturile si 
, iar marimea:
se numeste t.e.m.
operationala corespunzatoare conditiilor initiale. In cazul conditiilor
initiale nule 
.
Cu precizarile facute, teoremele lui Kirchhoff sub forma operationala se vor scrie:
si
.
Se
noteaza:
, numita impedanta proprie operationala a laturii si se scriu teoremele lui Kirchhoff sub forma:
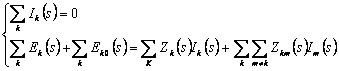
Se observa analogia formala dintre ecuatiile (8.109) si ecuatiile lui Kirchhoff pentru regimul stationar. Aceasta are drept consecinta extinderea formal neschimbata la studiul regimurilor variabile a tuturor metodelor de calcul ale circuitelor: metoda curentilor ciclici, metoda potentialelor la noduri, metoda impedantelor echivalente etc.
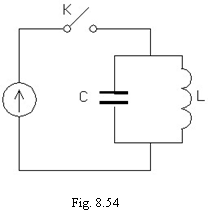Exemplu: sa se studieze variatia in timp a curentului si
tensiunii la bornele condensatorului in circuitul din figura 8.54 dupa deschiderea la t = 0 a intrerupatorului K.
T.e.m corespunzatoare conditiior initiale este:
,
iar ecuatia operationala a circuitului rezulta:
de unde:
Se noteaza: 
si
, rezultand
expresia operationala
a curentului:
,
expresie care se descompune in fractii simple:
Se utilizeaza acum teorema deplasarii si se obtine:
Forma operationala a tensiunii la bornele condensatorului este:
,
de unde, cu aceleasi notatii se obtine:
si
,
care conduce la expresia:
Metoda raspunsului tranzitoriu
O marime care evolueaza in timp dupa o lege oarecare
(fig.8.55) poate fi aproximata ca o succesiune de marimi in treapta,
retardate unele fata de altele cu 
.
Aproximatia este cu atat mai buna cu cat intervalele de timp sunt mai mici si
cu cat numarul treptelor este mai mare.
Se demonstreaza ca prima treapta 
, unde 
este functia treapta unitate, determina o
marime de iesire 
, 
fiind raspunsul la functia treapta unitate. Se
demonstreaza, in continuare, ca treptele retardate determina cate o marime de
iesire de forma:
(8.110)
stabilita in cazul in care intervalul de timp tinde catre 0 si numarul treptelor catre infinit.
Prin aplicarea principiului superpozitiei se poate scrie:
. (8.111)
Marimea de iesire este deci exprimata prin integrala Duhamel care se mai poate scrie sub oricare din formele:
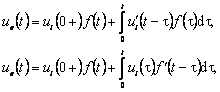
sau
Metodologia de calcul va fi urmatoarea:
- se determina raspunsul sistemului la o marime de intrare treapta unitara;
- se determina marimea de iesire cu ajutorul integralei Duhamel.
Exemplu: sa se determine expresia curentului tranzitoriu al unui circuit RL serie
supus tensiunii 
.
Expresia generala a curentului este:
unde:
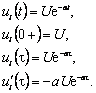
Pentru circuitul RL serie raspunsul la tensiunea treapta unitate (E=1V) este:
si
Rezulta:
Efectuand calculele deducem:
Metoda transformatei Fourier
Se numeste transformata Fourier a functiei 
, functia 
definita de relatia:
.
Transformarea inversa este definita de:
.
Notandu-se 
se scrie:
se numeste spectrul
functiei .
Este usor de vazut ca transformata Fourier si
transformata Laplace ale unei functii de timp au expresii analoge, transformata
Fourier obtinandu-se din transformata Laplace prin simpla inlocuire a lui 
cu 
.
In consecinta, metodologia de calcul a proceselor tranzitorii cu ajutorul transformarii Fourier va fi analoga:
- se determina spectrul marimii de intrare 
;
- se determina spectrele impedantelor laturilor;
- se determina spectrele curentilor din laturi;
- prin transformari inverse se determina expresiile valorilor instantanee ale curentilor.
Exemple
i) conectarea circuitului R, L pe o sursa de tensiune constanta E.
Impedanta spectrala a circuitului este:
iar intensitatea curentului rezulta din ecuatia:
Calculandu-se integrala prin metoda reziduurilor se obtine:
ii) conectarea circuitului R, L pe o sursa de tensiune sinusoidala.
Fie 
.Conform
identitatii lui Euler se poate scrie:
Deoarece marimile din paranteza sunt complex conjugate se lucreaza numai cu una din ele si se ia dublul partii reale a rezultatului:
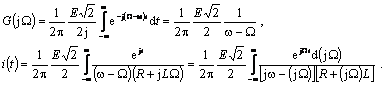
Integrala se calculeaza prin metoda reziduurilor.
Notandu-se: 
cu 
si 
, se obtine:
|
