Comportarea in regim dinamic a mijloacelor de masurare

Comportarea in regim dinamic a mijloacelor de masurare

Deoarece in multe situatii mijloacele de masurare trebuie sa urmareasca succesiunea in timp sau variatiile bruste ale masurandului prezinta importanta si comportarea in regim dinamic a acestora. Dependenta dintre marimea de intrare si de iesire la mijloacele de masurare privite ca sisteme poate fi descrisa prin ecuatii diferentiale care pot fi examinate atat in domeniul timp cat si in domeniul frecventa. Pentru cazul general ecuatia diferentiala care descrie comportarea mijloacelor de masurare este o ecuatie diferentiala liniara neomogena cu coeficienti constanti de forma:

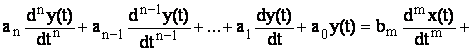
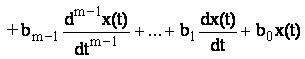(3.4)

Solutia ecuatiei diferen 636i82g tiale pentru cazul general are forma:

(3.5)

Primul termen corespunde regimului permanent, daca exista acest regim, indiferent daca este static sau dinamic si se numeste si solutia fortata a ecuatiei diferentiale, iar al doilea termen corespunde regimului dinamic tranzitoriu si se mai numeste si solutia libera a ecuatiei diferentiale. Din punct de vedere matematic, primul termen este o solutie particulara a ecuatiei diferentiale, iar cel de-al doilea termen este solutia ecuatiei diferen 636i82g tiale liniare omogene:

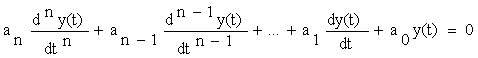(3.6)

Solutia ecuatiei (3.6) este de forma:

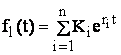(3.7)

unde: K_i sunt constante de integrare si se determina din conditiile initiale, iar r_i sunt radacinile ecuatiei caracteristice atasate ecuatiei diferentiale, de forma:

(3.8)

Ecuatia diferentiala se mai poate rezolva in anumite cazuri particulare cu ajutorul metodei operationale a transformatei Laplace.

3.3.1. Mijloace de masura de ordinul intai (MM I)

Ecuatia ce descrie functionarea unui MM I este, de forma:

(3.9)

Pentru demonstrarea proprietatilor MM I se utilizeaza o alta forma a ecuatiei diferentiale si anume se imparte intreaga ecuatie (3.9) cu a si se obtine:

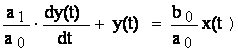(3.10)

unde: 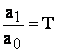- constanta de timp a MM I (raportul are dimensiuni de timp);

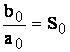- sensibilitate stationara (constanta ).

Cu aceste doua notatii ecuatia MM I devine:

(3.11)

3.3.1.1. Caracteristicile de frecventa

Se aplica operatorul Laplace ecuatiei diferentiale (3.11) si se obtine functia de transfer:

= (3.12)

Din (3.12) se obtine sensibilitatea complexa de frecventa:

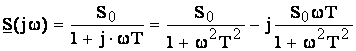(3.13)

Relatia (3.13) reprezinta functia sensibilitatii complexe de frecventa, de variabila w. Reprezentarea grafica in planul complex, respectiv hodograful functiei, este un semicerc, de diametru S₀ (fig. 3.4). Pentru w = 0 se obtine intersectia cu axa reala in punctul de coordonate (S₀, 0), iar pentru se obtine punctul de origine al planului complex (0,0). Aceste valori se deduc din inlocuirea valorii lui w in expresia (3.12).

Caracteristica amplitudine - frecventa este:

(3.14)

Functia (3.14) este reprezentata in fig. 3.5. Se observa caracterul de filtru trece - jos al MM I ( odata cu cresterea frecventei are loc o atenuare puternica a amplitudinii, astfel ca pentru valori mari ale lui w amplificarea este practic zero).

Caracteristica faza - frecventa

(3.15)

Pentru , valoarea functiei este 0, iar pentru valoarea functiei este:. Graficul functiei este redat in fig. 3.6.

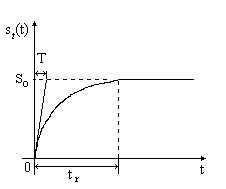
Fig. 3.6. Caracteristica faza - Fig. 3.7. Caracteristica sensibilitatii

frecventa a MM I. tranzitorii a MM I.

3.3.1.2. Caracteristicile de timp

Sensibilitatea tranzitorie

Inlocuind in ecuatia (3.11) semnalul de intrare cu semnalul treapta unitara, deci , vom nota si se obtine:

(3.16)

Solutia sensibilitatii tranzitorii este:

(3.17)

Caracteristica este reprezentata in fig.3.7. Curba este o exponentiala care are valoarea 0 la t = 0 si valoarea pentru (numita si valoare stationara). Tangenta in origine la caracteristica, se intersecteaza cu valoarea stationara dupa o durata de timp egala cu constanta de timp T a MM I. Durata de timp de la aplicarea semnalului treapta unitara pana la atingerea nivelului stationar se numeste timp de raspuns (sau timp de stabilizare t_s

Sensibilitatea pondere

Inlocuind, in ecuatia (3.11), semnalul de intrare cu semnalul impuls unitar, deci , vom nota si se obtine:

(3.18)

Rezolvarea ecuatiei diferentiale (3.40) se poate face cu ajutorul metodei operationale. Se aplica operatorul Laplace intregii relatii si se obtine:

sau 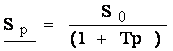(3.19)

Functia sensibilitatii pondere se obtine aplicand operatorul Laplace invers asupra relatiei (3.19) si se obtine:

(3.20)

Graficul sensibilitatii pondere este prezentat in fig. 3.8.

Si la aceasta caracteristica se remarca ca tangenta in zero, intersecteaza axa 0X dupa o perioada de timp egala cu constanta de timp T a MM I. Valoarea maxima a sensibilitatii pondere se numeste sensibilitate balistica si in cazul nostru este egala cu:

(3.21)

Mijloace de masurare de ordinul II (MM II)

Ecuatia diferentiala ce descrie functionarea unui MM.II este de forma:

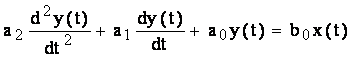(3.22)

Impartind toata ecuatia (3.22) cu a₂ se obtine:

(3.23)

Se noteaza:

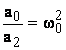sau 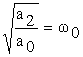(3.24)

unde w este pulsatia oscilatiei libere a MM II. Daca notam cu T₀ perioada oscilatiei libere a MM II avem:

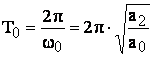(3.25)

Se noteaza:

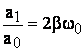- unde b se numeste grad de amortizare

Inlocuind w se obtine:

(3.26)

Ultimul termen se inmulteste si se imparte cu a₀:

unde: 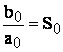- sensibilitatea in curent continuu (constanta)

Cu aceste notatii forma ecuatiei MMII este:

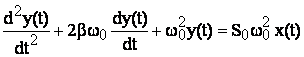(3.27)

3.3.2.1. Caracteristici de frecventa

Caracteristica sensibilitatii complexe de frecventa

Se aplica operatorul Laplace ecuatiei (3.27) si se obtine:

(3.28)

iar functia de transfer este:

(3.29)

Sensibilitatea complexa de frecventa se obtine din functia de transfer:

(3.30)

Relatia obtinuta reprezinta functia sensibilitatii complexe de frecventa, de variabila w si parametru b. Reprezentand in planul complex pentru wI ¥) si diferite valori ale parametrului b se obtine o familie de curbe (fig.3.9).

Pentru w = 0 toate curbele au punctul comun (S₀,0) pe axa reala iar pentru w ¥ toate curbele au punctul comun (0,0), originea planului complex.

Caracteristica amplitudine - frecventa

(3.31)

Caracteristica depinde de parametrul b pentru wI ¥). Se obtine de asemenea o familie de functii, reprezentata in figura 3.10.

Caracteristica faza - frecventa

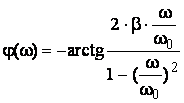(3.32)

Caracteristica depinde de parametrul b pentru wI ¥

Familia de functii este reprezentata in figura 3.11.

3.3.2.2. Caracteristicile de timp

Sensibilitatea tranzitorie

Aplicand la intrarea MMII un semnal treapta unitara x(t)=h₀(t), vom obtine functia sensibilitatii tranzitorii (y(t)=s_t(t)).

(3.33)

Solutia ecuatiei diferentiale (3.33) are doua componente, o componenta fortata si o componenta libera.

Un caz particular pentru solutia fortata este:

s_t(t)_t=S₀

Pentru determinarea solutiei libere, avem:

(3.34)

Ecuatia caracteristica este:

(3.35)

Radacinile ecuatiei caracteristice sunt:

(3.36)

Daca:

1. 0<b<1 radacinile sunt complexe. Solutia libera va fi de forma:

2. b radacinile sunt reale si egale. Solutia libera va fi de forma:

(3.38)

3. b> radacinile sunt reale si distincte. Solutia libera va fi de forma:

Constantele se determina din conditiile initiale impuse solutiei totale s_t(t) la momentul t=0 si primei derivate la acelasi moment. Se considera conditii initiale nule:

si (3.40)

Datorita valorilor pe care le poate lua gradul de amortizare b in intervalul [0, +¥), vom avea urmatoarele regimuri de functionare ale MMII:

1. 0<b<1. Solutia sensibilitatii tranzitorie este de forma:

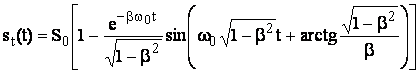(3.41)

Regimul se numeste oscilant amortizat

2. b=1.Solutia sensibilitatii tranzitorie este de forma:

(3.42)

Regimul se numeste aperiodic critic.

3. b>1. Solutia sensibilitatii tranzitorie este de forma:

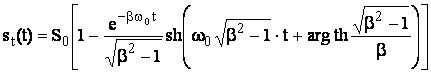(3.43)

Regimul se numeste aperiodic supraamortizat.

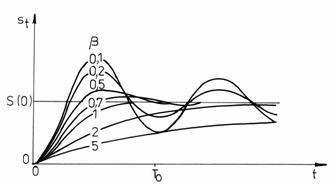
Fig. 3.12. Caracteristicile sensibilitatii tranzitorii ale MM II.

Solutia ecuatiei (3.33) este o familie de functii avand ca si parametru coeficientul de amortizare, ele fiind reprezentate grafic in fig. 3.12.

Sensibilitatea pondere

Aplicand la intrarea unui MMII un semnal impuls unitar(x(t) = d(t)) vom nota y(t) = s_p(t) si obtinem:

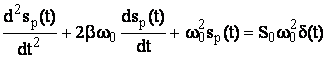(3.44)

Ecuatia diferentiala se poate rezolva cu ajutorul transformatei Laplace. In urma rezolvarii ecuatiei diferentiale (3.44) si datorita valorilor pe care le poate lua gradul de amortizare b in intervalul [0, +¥), avem trei regimuri:

1. 0<b<1. Solutia sensibilitatii pondere este de forma:

(3.45)

Regimul se numeste oscilatoriu amortizat.

2. b=1.Solutia sensibilitatii pondere este de forma:

(3.46)

Regimul se numeste aperiodic critic.

3. b>1. Solutia sensibilitatii pondere este de forma:

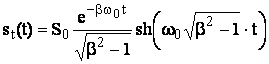(3.47)

Regimul se numeste aperiodic supraamortizat.

Solutia ecuatiei (3.44) este o familie de functii avand ca si parametru gradul de amortizare, ele fiind reprezentate grafic in fig. 3.13.