Vom considera fluidul ca un mediu continuu, deci vom presupune ca orice volum elementar dV de fluid contine un numar foarte mare de particule, dimensiunile elementului de volum fiind foarte mari in raport cu distantele dintre particule care compun fluidul.

Deplasarea unei mase de fluid constituie un curent de fluid. Aceasta este cunoscuta cand se cunoaste, in fiecare moment si in fiecare punct al curentului, valorile urmatorilor parametri: viteza v, densitatea r si presiunea p.

Intr-o curgere stationara, traiectoria deschisa de un punct din masa fluidului, in cursul miscarii sale, constituie o linie de curent. Vectorul viteza intr-un puncteste deci tangent la linia de curent care trece prin acel punct. Liniile de curent alcatuiesc o familie de linii de camp pentru campul de viteze. Ansamblul liniilor de curent care trec prin punctele unei curbe inchise constituie un tub de curent. Curgerea unui lichid printr-o conducta prezinta doua tipuri limita de regimuri de curgere. In cazul curgerii laminare, elementele de volumde fluid se misca regulat si paralel. Curgerea laminara pote fi potentiala sau turbionara, dar in acest caz, turbionele sunt dispuse regulat fata de directia generala de curgere. In cazul curgerii turbulente, turbioanele sunt dispuse dezordonat fata de directia genarala de curgere si liniile de curent sunt asezate neregulat unele fata de celalalte.

Cantitatea de fluid care strabate in unitatea de timp o anumita arie constituie fluxul de fluid sau debitul de fluid prin acea arie. Se deosebesc un debit de volum, respectiv un debit de masa, dupa cum cantitatea de fluid se exprima in volum, respectiv in masa. Daca Qv este debitul de volum, Qm debitul de masa si r densitatea fluidului, se pote scrie:

Qm=rQv (2)

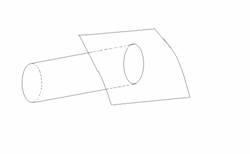Din fig. I rezulta, evident, ca debitul de volum al unui fluid printr-un element de arie dS dintr-o suprafata S este egal cu volumul fluidului continut intr-un cilindru drept cu baza dS si cu inaltimea numeric egala cu viteza v, deci

dQv=vdS fig. I

care se mai poate scrie, daca generatoarele cilindrului nu sunt paralele cu v, sub forma produsului scalar   

dQv=v d (3')

aria dS capatand un caracter vectorial vectorul respectiv fiind purtat pe narmala la elementul dS in sensul pozitiv. Debitul de masa prin elementul dS este deci

dQm=rv dS (3")

Sa consideram un tub de curent a carui sectiune sa aiba o arie destul de mica incat in diferitele puncte ale ariei viteza sa aiba aceeasi valoare. Viteza in diferitele puncte ale liniilor de curent fiind tangenta la aceste linii, fluidul nu poate parasi tubul de curent si, deci, in cazul unui fluid incompresibil, debitul de volum este acelasi, oricare ar fi sectiunea tubului de curent. Din (3') rezulta

dS= const.

Relatia (4) reprezinta ecuatia de continuitate in cazul fluidului incompresibil.

Sa considaram un volum V din fluid, limitat de suprafata inchisa S. Masa totala de fluid care iese pe secunda din suprafata S este

òå rv å (5)

integrala fiind intinsa asupra intregii suprafete.

Daca in interiorul suprafetei å nu sunt surse de fluid, Qm este egal cu cantitatea cu care scad in unitatea de timp, masa de fluid din volumul V, deci

òå rv då= - òV rdV (6)

integrala din membrul al doilea fiind intinsa asupra intregului volum V. Cu ajutorul formulri lui Green

òå rv då òV div (rv)dV

putem pune relatia (4) sub forma

òV + div (rv) dV=0 (6')

Ecuatia (6') trebuind sa fie satisfacuta oricare ar fi volumul V, rezulta

+ div (vr

forma mai generala a ecuatiei de continuitate .In cazul unui fluid incompresibil (4') devine

div v=0 (4")

Sa introducem marimea

rv   

numita densitate de flux. Ecuatia de continuitate se pote scrie si

+ div j=0

Mai putem da inca o forma ecuatiei de continuitate folosind relatia

Ñ rv)=rÑv + vÑr r div v + grad r

obtinem

+ r div v + v grad r

Obsevam ca ecuatia de continuitate este o relatie pur matematica; cu ajutorul ei poate fi determinat fluxul (debitul) de fluid printr-o suprafata, deci viteza fluidului. Ea nu face, insa, sa intervina, sub nici o forma (forte, presiuni) cauzele care produc miscarea fluidului.

Pe langa ecuatia de continuitate se mai poate obtine o relatie intre care caracterizeaza un fluid in miscare. Fie V un volum de fluid, limitat de o suprafata å. Fie p presiunea care se exercita asupra elementului de arie då al suprafetei å Forta totala care actionaza asupra volumului V, indreptata spre interior, este

F= - òS rdS

sau

F= - òV grad pdV

Aceasta forta poate fi considerata ca rezultanta unor forte elementare dF= - grad pdV aplicate diferitelor elemente de volum din V.

Ecuatia miscarii, pentru masa de fluid din unitatea d volum, se scrie

r = - grad p + f

f fiind pe unitatea de masa (f=rF). Daca forta f este datorata propriei greutati a unitatii de masa de fluid, (9) devine

r = - grad p + rg (9')

Viteza fiind o functie de timp si de coordonatele punctului din interiorul fluidului, avem

care, simbolic, se pote scrie

Deriva totala a vitezei in raport cu timpul este o suma a doua parti: una care corespunde variatiei, in timpul dt, a vitezei intr-un punct fix din fluid si una, la un moment dat t, care corespunde unei variatii pe distanta dreptei pe care se misca masa de fluid in timpul dt. Ultima relatie se mai scrie

v grad) v

astfel incat ecuatia de miscare devine

+ (v grad) v = - grad p (10)

care generalizeaza ecuatia (9). Relatia (10) este ecuatia fundamenata a mecanicii fluidelor si se numeste ecuatia lui Euler. Daca asupra fluidului actioneaza si campul de gravitatie, deci daca tinem seama de greutatea fluidului, (10) devine

+ (v grad) v = - grad p + g

in cazul fluidului in repaus, v=0, deci, in lipsa oricarei forte externe rezulta

deci p= const, pentru orice punct din masa fluidului. Daca asupra in repaus actioneaza campul de gravitatie, (10') devine

- grad p + g = 0

deci

grad p=rg

adica regasim relatia (11) pB - pA rgh caci daca, consideram axa Ox inreptata in sus,

= 0; = 0; = - rg

deci

p= - rgz+ const ,

sau pB - pA rgh, pB si pA fiind doua puncte in masa fluidului, situate, deasupra unui nivel de baza, la inaltimile zA si zB, iar h=zA - zB, poate fi pusa sub forma

v= grad F

sau

v = i + j + k

In cazul unei scurgeri stationare, deci cand intr-un punct din masa fluidului viteza nu depinde de timp, =0 si ecuatia lui Euler devine

(v grad)v= -     grad p + f

f fiind, ca si in (11), forta pe unitatea de masura de fluid. Obtinem

(v grad) vx +

sau

(v grad) vx + + = =

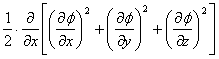
si alte doua expresii analoage pentru (v grad) vy si (v grad) vz. Aceaste expresii pot fi puse sub forma

(v grad)vx (

(v grad)vy = (

(v grad)vz = (

deci

(v, grad)v = grad ( (12)

Daca introducem marimea

r

p ò (13)

putem, deci, scrie

grad p grad p

si, daca tinem seama ca

f = - grad U,

relatia (12) devine

grad (U + p (33)

sau

U + p = const (34)

Relatie care exprima, sub o forma mai generala, ecuatia lui Bernoulli. Pentru un fluid incompresibil, r nedepinzand de presiune, = 0, deci

p , si (34') se scrie

U + + =const. (35)

Aceasta relatie se aplica in lungul unei linii de curent oarecare, iar in cazul unei curgeri fara turbioane, valoarea constantei nu depinde de linia de curent respectiva.

Ecuatia lui Bernoulli pentru unitatea de masa de fluid (35) se scrie, pentru unitetea de volum

rU + p + =const. (35')

Se vede ca ea exprima legea conservarii energiei mecanice, in curgerea fluidului:

reprezinta energia cinetica a unitatii de volum, rU energia potentiala, iar p presiunea corespunzatoare lucrului mecanic efectuat de catre forta care actionaeza asupra unitatii de volum pentru a o deplasa printr-o sectiune a conductei parcurse de fluid.

In campul de gravitatie, (35') se scrie

rgh + p + = const (35 ")

sau

h + = const (35 ''')

In ultima relatie, fiecare termen are dimensiunea unei lungimi; h reprezinta inaltimea la care se gaseste masa de fluid, o marime numita inaltime piezometrica, iar o marime numita inaltime dinamica. In cazul particular al unei conducte orizontale, h = const si (35") devine

p + = const = p

p fiind valoarea presiunii intr-un punct in care v = 0. Marimea p din (35 ") se numeste presiune statica, iar presiune dinamica. Suma lor este o constanta in lungul unei conducte orizontale.

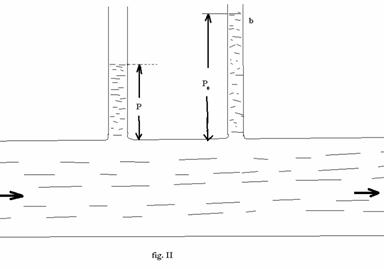
Presiunea statica se masoara cu un manometru alcatuit dintr-un tub vertical, in care lichidul manometric este insusi lichidul care curge prin conducta. Presiunea dinamica se masoara cu un instrument numit tub Pitot, alcatuit dintr-un tub indoit in unghi drept, una din ramuri fiind introdusa in conducta, in calea fluidului (fig. II: a - tub manometric; b - tub Pitot), cu deschiderea in sensul opus sensului de curgere. Fluidul, care patrunde in tubul Pitot este oprit brusc.Presiunea masurata cu tubul manometric al tubului Pitot este deci p . Scazand din aceasta valoare presiunea p, masurata cu manometrul, se obtine presiunea dinamica. Din relatia (36) rezulta ca, atunci cand viteza creste, presiunea dinamica crescand, presiunea statica p scade. Pe de alta parte, din (3) rezulta ca, cu cat sectiunea uneiconducte scade cu atat viteza creste, deci ca presiunea statica creste, respectiv scade,in acelasi timp cu sectiunea conductei. Acest fenomen este folosit intr-un instrument de masura a vitezei fluidelor in conducte, numit tub Venturi. Tubul Venturi este alcatuit 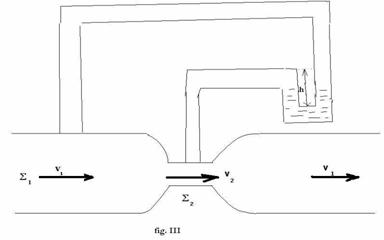dintr-un tub cu o sectiune å mai mica decat sectiunea å a conductei pe care este montat, de care este legat prin doua portiuni in forma de trunchi de con. In dreptul celor ramuri ale unui manometru in forma de U, care contine un lichid cu densitatea r (fig. III). Denivelarea h a lichidului in cele doua ramuri ale manometrului da valoarea diferentei

Dp = r gh

r fiind densitatea fluidului care curge prin conducta. Cum v å = v å conform ecuatiei de continuitate, rezulta

r gh =

sau

v = C   

unde

C = 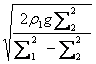este o constanta a aparatului.