ELECTROMAGNETISM (FENOMENE, LEGI, ECUATII)

tehnica mecanica

ALTE DOCUMENTE

COMPANIA NAŢIONALĂ ROMTEHNICA S

INMARSAT SI RADIOBALIZE IN SISTEMUL GMDSS

UTILIZAREA TRANSFORMATOARELOR DE MASURARE IN CIRCUITE TRIFAZATE FARA CONDUCTOR NEUTRU

Castrol EDGE 5W-30

Standard International de Practica in Evaluare 1 - GN 1 Evaluarea proprietatii imobiliare

CONCEPTUL DE SISTEM INFORMATIC

Distribuitoare hidraulice

EXTRAGEREA UNEI MOSTRE DE FUM DIN MAGAZIA DE MARFA

Castrol Enduron 10W-40

PROIECT DIPLOMA CALIFICARE PROFESIONALA TEHNICIAN MECANIC IN ITRETINERE SI REPARATII - INTRETINEREA SI REPARAREA CUTIEI DE VITEZE

- se calculeaza inductia, respectiv intensitatea campului electric rezultant ;

- se calculeaza potentialul :

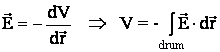
si se pun conditiile initiale pentru calculul concret al constantei de integrare.

Metoda Gauss este o metoda usor de aplicat, calculele fiind extrem de simple. Singura conditie este aceea ca simetria problemei sa permita alegerea unei suprafete inchise (eventual din categoria celor amintite mai sus).

c) Metoda ecuatiei Poisson :

- se cunosc distributiile volumice de sarcina electrica ;

- se scrie ecuatia Poisson :

ecuatie diferentiala neomogena de ordinul doi ;

- se cauta solutii ale acestei ecuatii, solutii care - odata gasite - permit calculul intensitatii campului electric (gradient al potentialului).

Observatie importanta : ecuatiile Poisson (si respectiv Laplace) se utilizeaza in cazul unor probleme de campuri electrostatice mai complicate, avand (obligatoriu, pentru rezolvarea integrala a acestora) conditii la limita (la frontiera) bine precizate.

Pe de alta parte, deoarece teoria ecuatiilor diferentiale neomogene nu este - inca - abordata la cursurile de specialitate, nu vom aplica aceasta metoda la rezolvarea problemelor care urmeaza.

Probleme rezolvate

Un fir rectiliniu infinit lung este incarcat cu densitatea lineica de sarcina =1mC/m. Considerand firul situat in vid, sa se calculeze :

a) Expresia intensitatii campului electric produs de fir intr-un punct situat la distanta D ;

b) Reprezentarea grafica E(D) ;

c) Sa se gaseasca o functie scalara de punct (in fapt potentialul electric) al carei gradient cu semn schimbat sa fie campul electric calculat anterior.

Rezolvare :

a) Prin metoda superpozitiei :

Doua elemente infinitezimale (simetrice fata de O) de lungime 'dr' produc in punctul M campul electric a carui intensitate este (vezi figura 1.23) :

Daca :

a a a

Se observa ca proiectiile pe directia Oy sunt egale si de sens contrar ; prin urmare rezultanta pe Oy este nula, in timp ce proiectiile pe axa Ox sunt egale si se insumeaza.

Campul total exista numai pe directia Ox si - datorita simetriei problemei - in loc sa integram de la -¥ la + ¥ se va considera in calcule (ca rezultat) dublul integralei de la 0 la +¥. Deci E_y
total = 0.

Integrala de mai sus este dificil de calculat datorita domeniului de variatie al lui r (intre 0 si + ¥). Prin urmare se impune o schimbare de variabila. Se observa ca atunci cand r variaza intre 0 si + ¥ unghiul a variaza intre 0 si p

Deci facand schimbarea de variabila :

rezulta :

adica :

si unitatea corespunzatoare de masura este .

Campul rezultant este proportional cu densitatea lineica de sarcina si invers proportional cu distanta D pana la fir.

Cu ajutorul legii lui Gauss :

Datorita simetriei problemei (in sensul ca in orice punct din spatiu - adica - si are aceeasi marime pentru toate punctele situate la aceeasi distanta D de fir) vom alege o suprafata cilindrica de raza D (ca in figura 1.24). Se observa ca exista flux al campului electric numai prin suprafata laterala (pentru care vectorul - normala la suprafata - si vectorul intensitate camp electric sunt omoparaleli (deci produsul lor scalar este diferit de zero - in fapt are valoare maxima !).

b) In ceea ce priveste dependenta grafica (D), ea este usor de realizat, intrucat se observa din relatia obtinuta la punctul anterior inversa proportionalitate a celor doua marimi (figura 1.25).

c) Deoarece pentru campul electrostatic :

Fie conditia initiala :

A) Pentru inceput ne ocupam de componenta E_x a campului creat de intregul fir. Integrala se va face - evident - cu y variind intre cele doua limite ale lungimii acestuia :

Exact ca pentru firul infinit lung vom recurge la o schimbare de variabila :

Prin urmare :

B) Pentru componenta E_y a campului electric generat de fir si evaluat in punctul M calculele sunt ceva mai simple (in sensul ca efectuarea integralei nu mai impune schimbarea de variabila anterioara / fara insa a evita complet acest procedeu). Astfel :

In functie de noua variabila 'u' se modifica si limitele de integrare. Prin urmare :

Observatie : Putem verifica rezultatul obtinut. Astfel, daca :

( genereaza dE_y pozitiv, in timp ce genereaza dE_y < 0) ;

(simetrie fata de axa Ox) Þ E_y = 0 .

Pentru calculul modulului campului electric rezultant din punctul M vom tine cont de faptul ca :

Unghiul pe care vectorul il face cu sensul pozitiv al axei Ox este :

Sa se gaseasca valoarea intensitatii campului electric intr-un punct oarecare al axei unei spire circulare de raza a, situata in vid, incarcata uniform cu .

a) Sa se efectueze calculele pentru = 10 ^-6 C/m, a = d = 1 m.

b) Sa se reprezinte grafic variatia lui |E| cu distanta in lungul axei.

Rezolvare :

a) Se observa din figura 1.27, urmarindu-se notatiile folosite, ca :

Totodata :

b) Pentru a aprecia dependenta intensitatii campului in functie de distanta d de centrul spirei , se stie ca :

Pentru d = 0 ; atunci cand d >> a , deci la distante mari inelul se comporta ca o sarcina punctiforma.

Sa se determine intensitatea campului electric si potentialul in cazul unei sfere conductoare de raza a, situata in vid, uniform incarcata cu r_S (densitate superficiala de sarcina electrica).

Rezolvare : ( teorema lui Gauss)

Din considerente de simetrie (figura 1.29), liniile de camp pornesc de la suprafata incarcata cu sarcina electrica - perpendicular pe aceasta suprafata - si sunt indreptate spre exterior.

Suprafata inchisa pe care se aplica legea lui Gauss este - de asemenea - o sfera concentrica cu sfera incarcata.

adica :

are directia si sensul lui (adica al lui , deci :

Se observa in relatia de mai sus ca ea poate fi scrisa in forma :

Pentru calculul potentialului - se stie ca :

deci :

Observatie : , ceea ce era de prevazut intrucat V(r) trebuie sa fie o functie continua (fiind derivabila), deci .

Se da o sfera de raza a = 1m , incarcata in volumul ei cu sarcina r_v (densitate volumica de sarcina) distribuita uniform , avand valoarea 1 mC/m³ (figura 1.30).

Se cere :

a) Campul electric in interiorul si in afara sferei ;

b) Potentialul electric in aceleasi conditii si reprezentarea grafica a celor doua marimi.

Rezolvare :

a) Ca si in cazul precedent, campul are simetrie sferica, deci se poate aplica Gauss :

Pentru r < a :

Pentru r > a :

b) Calculul potentialului se face tot separat, corespunzator celor doua regiuni.

Pentru r > a :

Pentru r < a :

Rezolvare

I. Metoda superpozitiei

Datorita simetriei problemei :

proiectiile campului electric pe axa Oy se anuleaza (vezi figura 1.33).

Pentru usurinta calculului ne propunem sa stabilim campul elementar creat - pentru inceput - de o suprafata elementara dS in punctul M :

pentru care studiem componenta :

Din figura 1.33 se observa ca zona desemnata cu notatia dS are suprafata :

Prin urmare :

Se observa ca intensitatea campului electric generat de o distributie plana infinita de sarcina electrica este independenta de distanta pana la plan. Cu alte cuvinte campul este uniform, perpendicular pe planul infinit si intensitatea lui are aceeasi valoarea in ambele parti ale acestuia (figura 1.34).

In cazul unui plan de dimensiuni finite, daca se neglijeaza efectele de margine (care exista !) se poate folosi - cu o buna aproximatie - relatia dedusa anterior.

Independenta dintre intensitatea campului produs de un strat de sarcini si distanta fata de plan a punctului in care se face evaluarea, a condus la ideea de a folosi un dublu strat de sarcini (ca in figura 1.35).

Campul dintre doua placi incarcate cu sarcini de semn contrar poate fi calculat ca rezultanta a campurilor generate de fiecare dintre cele doua plane. Aproximarea (in ceea ce priveste efectele de margine, vezi figura 1.36) este cu atat mai buna / corecta cu cat distanta dintre placi este mult mai mica decat dimensiunea acestora.

Revenind la situatia din figura 1.33, apare evident faptul ca :

si :

Observatie. In interior, acolo unde , se observa ca potentialul intr-un punct 'x' oarecare plasat intre cele doua placi este :

ceea ce inseamna ca atunci cand x creste V_(x) scade liniar.

Daca x = d , atunci (relatie deja cunoscuta pentru campul electrostatic uniform.

II. Metoda Gauss

Alegem ca suprafata inchisa suprafata exterioara a unui cilindru (pentru care raza bazei poate varia de la 0 la +∞).

Cilindrul fiind infinit, din simetrie se observa ca intensitatea campului este aceeasi pe ambele parti ale planului. Deoarece stim deja ca el este perpendicular pe plan, se observa ca fluxul prin suprafata laterala a cilindrului este nul (). In schimb, pe cele doua 'capace' (baze) ale acestuia se poate scrie (vezi figura 1.37) :

dar sarcina 'inchisa' in cilindru (existenta pe plan) este egala cu :

ceea ce implica (prin scrierea teoremei lui Gauss) :

adica : , orientat perpendicular pe plan (deci perpendicular pe bazele cilindrului ales).

Rezultatul este - asa cum era de asteptat identic cu cel anterior dar a fost obtinut in urma unui calcul mult simplificat. (Este foarte adevarat ca peste etapa consideratiilor de natura fizica, care tin cont de eventualele simetrii ale problemei si de consecintele acestora - gen anularea componentei tangentiale a intensitatii campului electric - nu se poate trece.)

Sa se determine

~~Sa se calculeze~~ capacitatea unui condensator plan, constituit din douaa straturi de dielectric de grosimi d₁ ssi d₂ , avand permitivitatatile electrice relative e_r1 ssi e_r2 ,dispuse paralel cu armaaturile de arie A.

Rezolvare

a) Campul produs de sarcina +q, egal distribuitaa pe un plan de arie A , se calculeazaa cu ajutorul legii lui Gauss. Suprafatta inchisaa corespunzaatoare este un paralelipiped care "imbracaa" complet planul incaarcat electric.

Liniile de camp, echidistante, sunt perpendiculare pe acest plan , iar sensul acestora este indreptat spre exterior.

Se poate observa, din figura 1.38~~care urmeaza~~, caa singurele suprafette care conteazaa sunt cele pentru care vectorii sunt coliniari.

Dacaa folosim observattia caa sarcina este egal distribuitaa pe suprafatta planaa A ssi trecem la nottiunea de densitate superficialaa de sarcinaa r_S : , obttinem

Dacaa aceeassi suprafatata este incaarcataa cu sarcinaa negativaa, campul electric (in modul) are aceeassi expresie, dar sensul vectorului camp electric este indreptat spre aceastaa suprafatata.

b) In cazul problemei date : atat , deci :

Deoarece prin definittie obttinem, in urma calculelor :

Se observaa caa relattia obtinutaa corespunde calculului unei capacitatati echivalente a douaa condsensrvatoare legate serie ; cele doua condensatoare au aceeasi arie A, grosimile d₁ si respectiv d₂ si permitivitatile e_r1 e_r2 (e ca si cum ar exista o armatura egala si paralela cu celelalte doua la interfata celor doi dielectrici) :

Sa se calculeze intensitatea campului electric (electrostatic) generat de un sistem de doua sarcini electrice egale si de semne contrare situate la distanta una de cealalta (dipol), intr-un punct oarecare M aflat la distanta R >>

Figura 1.40

In punctul M (considerat foarte departe de dipol) campul creat de perechea celor doua sarcini are expresia generala :

Deoarece distanta dintre dipol si punctul in care se calculeaza ampul este mult mai mare decat distanta dintre cele doua sarcini (egale si de sens contrar) putem recurge la urmatoarele aproximatii :

In aceste conditii :

Dar - in continuare - putem tine cont de marimile introduse in cazul dipolului ideal si de aproximarile initiale :

In consecinta :

Se observa in expresia obtinuta faptul ca acest camp apare drept rezultanta vectoriala a doua campuri (vezi figura 1.41), respectiv :

Figura 1.41

= componenta radiala ;

= componenta antiparalela cu

Observatii :

Deoarece campul rezultant este - in fiecare punct - tangent la linia de camp, putem vizualiza constatarea anterioara asa cum se arata in figura 1.42

Expresia obtinuta arata si faptul ca marimea intensitatii campului electric generat de dipol scade proportional cu R ; prin urmare, comparativ cu intensitatea campului general de o sarcina libera (vezi figura 1.43) efectul existentei unui dipol se simte pe o distanta mult mai redusa.

Figura 1.

b) Campul electric generat de un dipol ideal intr-un punct M plasat la distanta R >> poate fi calculat si prin intermediul potentialului electric

Folosim proprietatea de aditivitate a potentialelor :

Deoarece :

potentialul din punctul M se aproximeaza cu relatia :

La limita (pentru dipolul ideal) si ; prin urmare :

Dar in electrostatica (in conditii conservative) intensitatea campului electric intr-un punct poate fi exprimata drept gradient cu semn schimbat al potentialului acelui punct :