ERORI DE MASURARE

Rezultatul unei masurari, oricat de precise ar fi aparatele de masura si metodele de masurare, nu coincide niciodata cu valoarea adevarata a marimii de masurat. Aceasta se datoreaza unor cauze obiective sau subiective care vor fi discutate in continuare.

Valoarea adevarata (reala) a unei marimi este valoarea exacta a marimii respective, care nu poate fi aflata experimental decat cu aproximatie. Rezultatul unei masurari individuale reprezinta valoarea masurata. Abaterea valorii masurate fata de valoarea adevarata a masurandului (marimii care se masoara) constituie eroarea de masurare.

2.1. Clasificarea erorilor de masurare

A. Dupa modul de calcul erorile pot fi : absolute, relative si raportate.

a) Eroarea absoluta este diferenta dintre valoarea masurata si valoarea adevarata a marimii masurate :

DX = X - X_e (2.1)

Eroarea absoluta are aceleasi dimensiuni fizice ca si marimea masurata si se exprima in aceleasi unitati de masura.

Eroarea absoluta cu semn schimbat se numeste corectie.

b) Eroarea relativa este raportul dintre eroarea absoluta si valoarea marimii masurate:

(2.2)

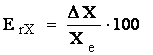(2.3)

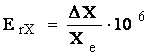[p.p.m.] (2.4)

Eroarea relativa poate fi exprimata ca un numar adimensional, in procente sau in parti pe milion (de ex., 2^.10 , sau 0,02% sau 200ppM).

c) Eroarea raportata este raportul dintre eroarea absoluta maxima si o valoare conventionala X_c a marimii de masurat:

[%] (2.5)

Valoarea conventionala poate sa fie intervalul de masura al unui mijloc de masurare (pentru mijloace de masurare cu scala liniara cum sunt voltmetrele si ampermetrele magnetoelectrice), unghiul de deviatie maxima (pentru mijloace de masurare cu scala neliniara cum sunt ohmetrele magnetoelectrice) sau chiar valoare indicata pentru mijloacele de masurare care nu au capat de scala (cum este contorul de inductie). Eroarea raportata se poate exprima in aceleasi moduri ca si eroarea relativa.

B. Dupa sursa de aparitie erorile se clasifica astfel:

a) Erorile de model sunt datorate fenomenului supus masurarii si ele provin din simplificarea sistemului fizic asupra caruia se efectueaza masurarea neglijandu-se unele proprietati sau marimi fizice caracteristice acestuia.

b) Erorile de influenta reprezinta erorile introduse de factorii de mediu care pot influenta marimea de masurat. Exemple: umiditatea mediului ambiant la masurarea grosimii hartiei cu grosimetre electrice capacitive,

c) Erorile instrumentale reprezinta erorile proprii ale mijloacelor electrice de masurare fiind cuprinse, de regula, intre limite cunoscute in functie de modul de definire a preciziei precum si erorile suplimentare datorita marimilor de influenta, de ex.: temperatura, campurile electromagnetice, umiditatea etc.

d) Erorile de interactiune dintre mijlocul electric de masurare si fenomenul supus masurarii sunt cauzate de actiuni electromagnetice sau mecanice exercitate de mijlocul de masurare asupra fenomenului supus masurarii si reciproc. Exemple: masurarea temperaturii folosind un traductor rezistiv de marime suficient de mare pentru ca sa perturbe temperatura ce se masoara, masurarea tensiunii electrice cu un voltmetru cu impedanta mica de intrare, etc.

sunt cauzate de neasigurarea de catre beneficiar a conditiilor nominale de utilizare a mijlocului electric de masurare. Exemple: alimentarea cu o tensiune cu mult diferita de intervalul nominal de tensiune, alimentarea cu o tensiune alternativa de frecventa mult diferita de intervalul nominal, folosirea in pozitie necorespunzatoare a mijlocului de masurare etc. Sunt erori subiective, care pot fi evitate printr-o cunoastere corecta a conditiilor de utilizare a mijlocului de masurare si prin citirea corecta a indicatiei acestora.

C. Dupa modul de manifestare la repetarea masuratorilor, care au loc in conditii practic identice, erorile se clasifica in:

a) erori aleatoare caracterizate prin aceea ca variaza imprevizibil in timp, ca durata si ca semn;

b) erori sistematice care se caracterizeaza prin aceea ca nu variaza in timp sau au o variatie lenta la repetarea masuratorilor;

c) erorile grosolane sunt caracterizate prin abateri mari (aberante) fata de celelalte valori ale sirului de valori masurate.

2.2. Erori aleatorii

Daca se repeta masurarea unei marimi in conditii practic identice (respectiv cu aceleasi mijloace si metode de masurare, de catre acelasi operator, sub actiunea acelorasi marimi de influenta, etc) se constata ca valorile masurate obtinute difera intre ele, rezultand un sir de valori masurate x , x , x_n

Daca nunarul de masuratori este foarte mare (teoretic infinit) prin reprezentarea grafica a frecventei de aparitie a valorilor masurate in cadrul sirului de valori in functie de valorile masurate se obtine o curba de forma celor din figura 2.1.

Eroarea aleatorie reprezinta abaterea valorilor masurate fata de valoarea adevarata a masurandului daca se considera ca erorile sistematice sunt zero. Deoarece erorile aleatorii variaza in mod imprevizibil ele nu pot fi eliminate prin corectii ci folosind legile statisticii este posibil doar sa se estimeze erorile limita despre care se poate afirma cu o anumita probabilitate ca nu vor fi depasite de erorile aleatoare.

Pentru tratarea matematica a erorilor aleatoare, se admite in general, ca distributia probabilitatii erorilor este data de legea normala a erorilor - numita si legea erorilor a lui Gauss:

(2.6)

unde: y - densitatea de probabilitate;

x - variabila aleatoare (valoarea masurata);

m - valoarea medie;

s - eroarea medie patratica.

Teoretic, cei doi parametrii m si s ai distributiei normale pot fi determinati cu formulele:

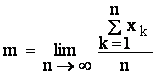, (2.7)

unde x_k reprezinta valorile masurate, ce formeaza sirul de valori.

Semnificatia fizica a marimilor m si s este urmatoarea:

-valoarea medie a unui sir de valori obtinute prin masurarea unei marimi de un numar foarte mare de ori (teoretic infinit) reprezinta chiar valoarea adevarata a acelei marimi;

-eroarea medie patratica ne arata gradul de afectare cu erori a valorilor obtinute din masuratori. Pentru ca un sir de masuratori sa fie cat mai bine efectuat este necesar ca eroarea medie patratica a acelui sir sa fie cat mai mica.

Legea normala de distributie, reda proprietatea de simetrie a erorilor aleatoare (erorile aleatoare cu semne diferite se intalnesc cu aceeasi probabilitate) si proprietatea de concentrare (erorile aleatoare mici in valoare absoluta apar mai frecvent decat cele mari). Aceste proprietati sunt caracteristice aproape tuturor cazurilor practice de masuratori.

Se demonstreaza prin calcule ca probabilitatea ca y sa ia valori in afara intervalului m3s este foarte mica, de 0,27%, ceea ce inseamna ca 99,73% din valorile masurate vor fi grupate in intervalul 3s fata de valoarea medie. De aceea valoarea 3s poate fi considerata ca eroare limita.

Aplicarea relatiilor (2.7), necesita un numar foarte mare de masuratori (peste 50 de masuratori) si de aceea se estimeaza parametrii m si s, pornind de la un numar relativ mic de masuratori (cel putin 4 - 5 masuratori).

In acest caz media m se estimeaza prin media aritmetica pentru un numar finit de masuratori

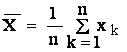(2.8)

si media aritmetica se considera ca rezultat al masurarii.

Eroarea medie patratica se estimeaza prin marimea:

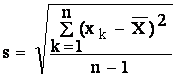(2.9)

care reprezinta eroarea medie patratica pentru un numar finit de masuratori.

Eroarea medie patratica a valorii medii se estimeaza prin:

(2.10)

Eroarea limita a mediei aritmetice obtinute dintr-un sir de masurari este:

(2.11)

unde t este un coeficient de amplificare ce reprezinta parametrul distributiei Student pentru o anumita probabilitate (nivel de incredere)(tab.2.1).

Rezultatul unei masuratori x_i se gaseste in intervalul [] cu o probabilitate p* asociata cu numarul de masuratori si valoarea parametrului t. De asemenea media a rezultatelor unui sir de masuratori se afla in intervalul [] cu aceeasi probabilitate p*, functie de n si t.

Probabilitatea p* se numeste nivel de incredere, marimile ,     se numesc limite de incredere, iar intervalele [], respectiv [] se numesc intervale de incredere.

In practica masurarilor nivelul de incredere se alege dupa criteriul importantei rezultatului (de exemplu in functie de consecintele posibile ale unui rezultat gresit). Astfel, in cazul masurarilor curente se poate alege un nivel de incredere de 0,90 sau 0,95, iar la masurarile de mare importanta se poate lua 0,9973.

Tabelul nu se cere pt. examen

Tabelul 2.1.

Estimarea erorilor totale pentru metodele indirecte de masurare

In cazul metodelor indirecte de masurare, valoarea marimii masurate se obtine in functie de alte marimi a, b, c, masurate direct, prin relatia:

X = f(a, b, c, ) (2.12)

Presupunand ca marimile sunt afectate de erori sistematice - erorile limita de masurare - Da, Db, Dc, - atunci marimea X se determina cu o eroare sistematica DX :

X+DX= f(a+Da, b+Db, c+Dc,)    (2.13)

de unde:

DX = f(a+Da, b+Db, c+Dc) - f(a, b, c, )    (2.14)

Dezvoltand in serie Taylor si neglijand termenii de ordin superior se obtine:

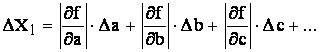(2.15)

unde toti termenii se iau in valoare pozitiva.

Eroarea relativa limita de masurare este deci

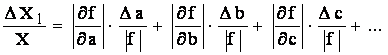
In tabelul 2.2 sunt prezentate formulele pentru calculul erorilor limita totale pentru unele formule intalnite curent.

Tabelul 2.2

CAPITOLUL 3

CARACTERISTICI GENERALE ALE

MIJLOACELOR DE MASURARE

3.1. Schema bloc a mijloacelor de masurare

Procesul de masurare presupune un proces de preluare a informatiei de masurare de la masurand sub forma unei energii, transmiterea acesteia la unitatea de prelucrare ce stabileste valoarea marimii masurate prin comparatie cu un etalon si o aplica unui bloc de iesire care poate avea si rol de indicator

Marimile pot fi active, daca sunt purtatoare de energie (ex. tensiunea, curentul electric, etc.) sau pasive daca informatia de masurare este continuta in structura masurandului (ex. densitatea, rezistenta, etc.).

Schemele bloc ale mijloacelor de masurare sunt specifice caracterului marimii de masurat; astfel pentru marimile active energia corespunzatoare informatiei de masurare poate fi preluata direct de la masurand, in timp ce pentru marimile pasive este nevoie de o sursa suplimentara de energie, capabila sa puna in evidenta (sa activeze) masurandul.

Schema bloc a mijloacelor de masurare a marimilor active este prezentata in fig. 3.1.

Fig.3.1. Schema de principiu a mijloacelor de masurare a marimilor active.

Informatia utila este preluata de la masurand de traductorul de intrare TI care o converteste astfel incat sa poata fi transmisa printr-o linie de transmisie LT unei unitati de prelucrare UP. In unitatea de prelucrare informatia de masurare este comparata cu valoarea inscrisa intr-o memorie M pe baza careia se stabileste valoarea masurata care este transmisa utilizatorului prin traductorul de iesire TE.

Schema bloc a mijloacelor de masurare a marimilor pasive este prezentata in fig. 3.2. Energia furnizata de sursa de energie SE actioneaza asupra masurandului prin intermediul unui sistem de activare SA. Semnalul de activare este explicat traductorului TI si modulat de masurand traductorului de intrare TI . Prin liniile de transmisiune LT si LT semnalele sunt transmise unitatilor de prelucrare UP si UT de la iesirile carora se aplica unui demodulator D.

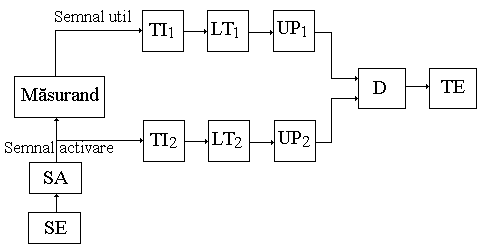
Fig.3.2. Schema de principiu a mijloacelor de masurare a marimilor pasive.

Demodulatorul are rolul de a elimina semnalul de activare si de a extrage informatia utila, proportionala cu valoarea masurandului, pe care o furnizeaza traductorului de iesire TE.

3.2. Caracteristici statice ale mijloacelor de masurat

Mijloacele de masurat trebuie sa realizeze o corespondenta biunivoca intre marimea de masurat x si rezultatul masurarii y. Pentru un regim stationar, independent de timp, dependenta celor doua marimi este descrisa de caracteristica statica de transfer (fig.3.3.).

Fig.3.3. Caracteristica statica de transfer a mijloacelor de masurare.

a)     analogice; b) numerice.

Din caracteristica de transfer rezulta o serie de caracteristici metrologice ale mijloacelor de masurare.

1. Rezolutia unui mijloc de masurare reprezinta cea mai mica variatie care poate fi apreciata la iesirea acestuia. Pentru mijloacele de masurare analogice este o fractiune dintr-o diviziune, iar pentru mijloacele de masurare numerice este un bit.

2. Sensibilitatea reprezinta raportul dintre variatia marimii de iesire si variatia corespunzatoare a marimii de intrare

(3.1)

unde: S este sensibilitatea, y - marimea de iesire, x - marimea de intrare a mijlocului de masurare.

3. Pragul de sensibilitate este cea mai mica variatie a masurandului care poate fi pusa in evidenta de catre mijlocul de masurare

Rezolutia caracterizeaza iesirea mijlocului de masurare, pragul de sensibilitate caracterizeaza intrarea mijlocului de masurare, iar sensibilitatea reprezinta o caracteristica de transfer a mijlocului de masurare.

4. Precizia este caracteristica metrologica a unei masurari ce exprima gradul de afectare a rezultatelor masurarii cu erori de masurare. Precizia si eroarea constituie un cuplu dihotomic. Precizia ridicata corespunde unei erori mici, respectiv precizia scazuta unei erori mari. Cantitativ, precizia este descrisa de eroare.

5. Intervalul de masurare reprezinta intervalul de valori ale marimii de masurat pe intinderea caruia un mijloc de masurare poate furniza informatii de masurare cu erori limita prestabilite. Intervalul de masurare este cuprins intre o limita inferioara X_min si o limita superioara X_max.

6. Capacitate de suprasarcina este capacitatea unui mijloc de masurare de a suporta fara defectiuni sarcini ce depasesc conditiile de referinta sau intervalul de masurare. In acest scop, prin constructia sa, un mijloc de masurare prezinta o capacitate de suprasarcina de lunga durata si una de scurta durata.

7. Puterea consumata reprezinta puterea preluata de la fenomenul supus masurarii pentru formarea semnalului metrologic si obtinerii valorii masurate si ea depinde de tipul convertorului de intrare, de ex., masa si dimensiunile traductorului, precum si de tipul convertorului de iesire, (de ex., instrumentele analogice consuma puteri intre cativa miliwati si wati, iar aparatele digitale puteri mai mici).

In cazul mijloacelor si a metodelor de masurare electrice destinate masurarii marimilor electrice, caracterizarea acestora din punct de vedere al consumului de energie se poate face si prin impedanta de intrare. Intre puterea consumata sau puterea de intrare, pe de-o parte, si impedanta interioara sau impedanta de intrare, pe de alta parte exista o legatura care depinde de structura mijloacelor si metodelor de masurare electrice.

8. Timp de masurare reprezinta intervalul de timp care se scurge de la aplicarea unui semnal treapta la intrarea unui mijloc de masurare si pana la stabilirea semnalului de iesire cu o abatere egala cu eroarea limita de masurare, fata de valoarea stationara a acestuia. De ex., pentru aparatele analogice timpul de masurare este maxim 4s. Pentru aparatele digitale se da viteza de masurare, de ex., 50 masurari / secunda.

9. Fiabilitate metrologica ne arata probabilitatea ca mijloacele de masurare sa functioneze corect, fara depasirea erorilor garantate prin clasa de precizie, un interval de timp determinat, cu respectarea conditiilor tehnice impuse de constructor.

Urmarind comportarea unui numar n₀ - suficient de mare - de mijloace de masurare electrice de acelasi fel, care functioneaza in aceleasi conditii, se constata ca numarul n al acelor mijloace de masurare electrice, ce si-au pastrat intre anumite limite proprietatile lor, scade necontenit odata cu trecerea timpului, prin alterarea proprietatilor lor, celelalte n₀ - n mijloace de masurare electrice considerandu-se defectate. Pentru a caracteriza ritmul defectarii mijloacelor electrice de masura se defineste rata defectarilor:

(3.2)

Se poate afirma, cu probabilitatea:

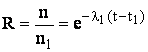(3.3)

ca un mijloc electric de masurare functioneaza bine dupa un interval de timp t - t₁ cuprins in perioada de viata utila. Aceasta probabilitate reprezinta fiabilitatea mijlocului de masurare electric. Fiabilitatea depinde de modul in care au fost concepute, realizate, pastrate, transportate si utilizate mijloacele de masurare electrice.

10. Stabilitatea reprezinta calitatea unui aparat digital de a-si pastra timp indelungat caracteristicile, prin conservarea zeroului si instabilitatea la variatiile de temperatura, umiditate si parazitii electromagnetici, de ex., ±0,01% pe an.

11. Compatibilitatea cu un sistem automat de masurare

Un aparat digital este compatibil cu un sistem automat de masurare daca este prevazut cu o interfata de intrari-iesiri cu ajutorul careia se poate conecta la liniile magistralei sistemului, pentru a primi comenzi si a furniza date in cod.