Exemplu de proces cu parametri distribuiti. Schimbatorul de caldura tubular în regim tranzitoriu

Se considera un schimbator de caldura tubular, la care se va studia regimul tranzitoriu indus la schimbari ale debitului de fluid, temperaturii de alimentare a fluidului sau temperaturii agentului termic. Pentru simplitate, temperatura agentului termic se considera uniforma în tot spatiul schimbatorului, situatie posibila atunci când agentul termic este abur saturat în condensare, un lichid la fierbere, sau un lichid supus unei agitari suficient de intense (fig 11).

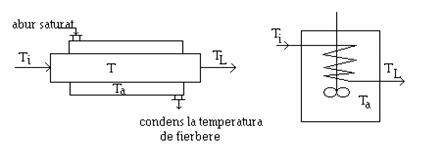
Fig. 11. Schimbatoare de caldura cu temperatura agentului termic uniforma spatial

Temperatura fluidului supus încalzirii sau racirii este dependenta de pozitia în lungul tevii si respectiv de timp. Modelul matematic ce exprima aceste dependente se obtine din ecuatia de bilant termic. În ipotezele ca circulatia fluidului în teava este de tip deplasare totala, nu au loc schimbari de faza, procesul este izobar si proprietatile fluidului sunt constante, aceasta ecuatie este de forma:

(97)

T, T_a - temperaturile fluidului si respectiv agentului termic;

r, c_p - densitatea si caldura specifica ale fluidului;

u - viteza de curgere a fluidului, presupusa constanta în raport cu z (ipoteza nu întotdeauna acceptabila);

z - coordonata axiala (în lungul tevii);

P, A - perimetrul si respectiv aria sectiunii transversale.

La tevi circulare (d_t - diametrul tevii).

Conditiile initiale si la limita asociate ecuatiei (97) sunt:

(98)

În scrierea ecuatiei (97) s-a considerat ca peretele metalic nu influenteaza dinamica schimbatorului (capacitatea calorica a peretelui metalic neglijabila). Ecuatia p 434b13e ermite calculul evolutiei temperaturii fluidului, T, în timp si în lungul axei schimbatorului. În continuare, se vor calcula evolutii generate de modificari ale temperaturii agentului termic, T_a, temperaturii de intrare a fluidului, T_i si respectiv vitezei u (debitului de fluid). Ecuatia (97) este o ecuatie diferentiala cu derivate partiale de ordinul I, care, daca debitul de fluid este variabil în timp, este neliniara si nu admite solutie analitica. O solutie aproximativa se poate obtine totusi pe cale analitica, prin liniarizarea ecuatiei diferentiale în jurul unei stari stationare. O astfel de solutie va fi dedusa în continuare, presupunând ca la schimbatorul se afla la starea stationara:

si .

Ecuatia (97) se transcrie în forma echivalenta:

; (99)

În regim stationar ():

(100)

Scazând (100) din (93) se obtine:

; ; ; (101)

Termenul neliniar se poate liniariza prin dezvoltare în serie Taylor, în jurul starii stationare:

(102)

Din (101) si (102) rezulta (cu w=u-u_s):

(103)

În regim stationar, evolutia temperaturii în lungul schimbatorului se obtine prin integrarea ecuatiei (100):

, sau (104)

(105)

Înlocuind (105) în (103) rezulta:

(106)

Ecuatia (106) este liniara si poate fi integrata pe cale analitica. Se va utiliza în acest scop metoda Transformatei Laplace. Transformata ecuatiei (106) în domeniul complex este:

(107)

Ecuatia (107) se integreaza în raport cu z prin metoda "variatiei constantei". În acest scop se rezolva ecuatia omogena corespunzatoare:

(108)

Aceasta are solutia:

(109)

Solutia ecuatiei (107) se considera de forma (109), în care constanta de integrare j devine o functie de z, ce urmeaza a fi determinata.

Din (109) si (107) rezulta:

(110)

Integrând în raport cu z se obtine:

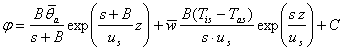(111)

C - constanta de integrare.

Înlocuind expresia lui j în (109) se obtine:

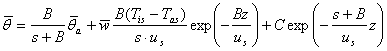(112)

Din conditia initiala: , rezulta:

(113)

Din (112) si (113) se obtine expresia solutiei ecuatiei liniarizate, în domeniul complex (Laplace):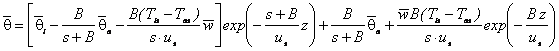 (114)

Introducând functiile de transfer:

(115)

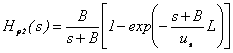(116)

, (117)

transformata Laplace a functiei are expresia:

(118)

Cei trei termeni ai expresiei astfel obtinute, reprezinta efectele individuale ale temperaturii de intrare, temperaturii agentului termic si respectiv vitezei fluidului (debitului) asupra temperaturii fluidului la iesirea din teava schimbatorului. În continuare, se vor calcula, cu ajutorul relatiei (118), evolutiile în timp ale temperaturii la iesirea din teava schimbatorului pentru modificari treapta ale celor trei variabile independente.

Analiza unor utilaje de transfer de masa operate în regim nestationar

Modelul matematic al unei coloane de rectificare discontinua a amestecurilor binare

Regimul de functionare este în acest caz nestationar prin natura intrinseca a procesului. Cantitatea de amestec din blaz si compozitia acestuia sunt continuu variabile în timp. Mentinerea constanta a compozitiei distilatului presupune cresterea continua a raportului de reflux al coloanei.

De asemenea, va exista o tendinta de reducere continua a debitului de vapori care circula prin coloana, ca urmare a cresterii continue a temperaturii de fierbere a amestecului din blaz (a carei concentratie în component usor este din ce în ce mai redusa, pe masura ce separarea avanseaza ).

Se considera procesul de separare a unui amestec binar, într-o coloana cu talere (fig. 14), pentru descrierea careia se introduc urmatoarele ipoteze simplificatoare:

n=1,2, N

în care:

L_n, V_n - debitele molare de lichid si respectiv vapori rezultate de pe talerul n;

H_n - cantitatea de amestec (retentia) pe talerul n al coloanei.

Debitul molar de vapori fiind constant în lungul coloanei: V_n+1=V_n=.=V.

Ecuatia (128) devine:

; n=1,2, N (129)

Bilantul masic partial al componentului volatil pe talerul n al coloanei este exprimat prin ecuatia:

; n=1,2, N

x_n, y_n - fractiile molare ale componentului volatil în fazele lichida si respectiv de vapori, continute pe talerul n al coloanei.

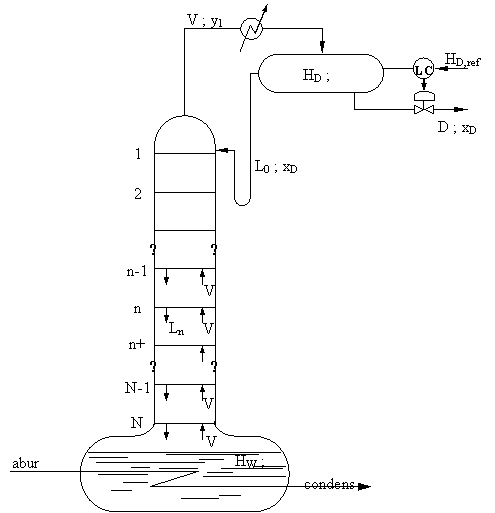
Fig. 14 Coloana de rectificare discontinua

Pentru blazul coloanei, cele doua ecuatii de bilant masic, total si partial, au expresiile:

(131)

(132)

Pentru rezervorul de reflux, ecuatiile de bilant masic sunt:

(133)

(134)

Din ipoteza echilibrului termodinamic lichid-vapori pe talerul n, în ipoteza comportarii ideale a celor doua faze, se pot scrie relatiile (date de legea Raoult):

(135)

; n=1,2, N

p - presiunea de lucru

P₁, P₂ - presiuni de vapori ale componentilor puri ai amestecului, la temperatura de lucru.

Din (135) si (136) se obtine relatia Fenske:

; n=1,2, N (137)

- volatilitatea relativa

Din punct de vedere hidrodinamic, se presupune ca debitul de lichid ce paraseste talerul n este suma între debitul ce deverseaza peste pragul talerului (L_n,p) si debitul ce se scurge prin orificiile talerului sub forma de picaturi (L_n,o). Acestea se pot calcula din relatiile semiempirice:

; n=1,2, N (138)

H_n,s - cantitatea statica (corespunzatoare regimului stationar) de lichid de pe talerul n.

; n=1,2, N (L_n,p = 0 pentru H_n < H_n,s). (139)

K₁, K₂ - constante obtinute experimental sau din relatii empirice

; n=1,2, N

Modelul matematic al coloanei este format din 2N+2 ecuatii diferentiale de bilant masic (128) - (134) din care se obtin prin integrare retentiile de lichid pe talere, H₁, H₂, ., H_N, cantitatile de lichid din blaz, H_w si rezervorul de distilat, H_D si respectiv concentratiile corespunzatoare ale compusului volatil, x₁, x₂, .x_N, x_w si x_D. Concentratiile în faza de vapori (y_n) se obtin din (137). Debitele de lichid L₁, L₂, ., L_N se calculeaza din relatiile hidrodinamice (138) - (140). Debitul de distilat, D, se obtine din principiul de functionare a regulatorului de nivel al rezervorului de distilat, iar debitul de reflux, L₀, se fixeaza în functie de puritatea dorita a distilatului obtinut la iesirea din condensatorul coloanei (x_D=y₁).

Debitul de vapori care circula prin coloana, V, este calculat din sarcina termica furnizata coloanei în refierbator (debitul de abur de încalzire).

Modelul matematic al unei coloane de rectificare continua în regim tranzitoriu

Se considera o coloana cu talere de rectificare a unui amestec binar, cu functionare continua (fig. 15). Regimurile tranzitorii apar la un astfel de utilaj în perioadele de pornire, oprire sau modificare a punctelor de functionare stationara (modificarea puritatii distilatului, schimbarea compozitiei sau debitului în alimentare etc).

Ecuatiile modelului matematic ce descrie regimul tranzitoriu al coloanei se obtin din bilantul masic al componentului volatil si respectiv bilantul termic pe talerele coloanei.

Ipotezele introduse în scrierea ecuatiilor de bilant sunt asemanatoare celor întâlnite la coloana de rectificare discontinua:

n=1,2, N

În zona de epuizare (sub talerul de alimentare), debitele de lichid si vapori sunt diferite fata de cele din zona de concentrare, fiind influentate de valoarea debitului de alimentare, compozitia amestecului alimentat, precum si de starea termica a alimentarii.

Bilantul componentului volatil pe talerul de alimentare este exprimat prin ecuatia (v. fig. 15b):

(142)

F, x_F - debitul molar de alimentare si respectiv fractia molara a componentului volatil în alimentare.

Fig. 15 Coloana de rectificare continua cu talere ; (a) coloana cu talere ;(b) talerul de alimentare.

Relatia între debitele ce intervin în ecuatia de bilant (142) se obtine din bilantul masic total în jurul talerului de alimentare:

(143)

Alte relatii între debitele de lichid si vapori ce intra si ies de pe talerul de alimentare, se obtin din ecuatia de bilant termic pentru acest taler.

Se noteaza:

i - entalpia amestecului alimentat (kJ/mol); i', i" - entalpiile lichidului, respectiv vaporilor la starea de saturatie (kJ/mol); i_vap - entalpia latenta de vaporizare a amestecului;

Starea termica a alimentarii, q, este definita prin relatia:

(144)

Din aceasta relatie se observa ca valoarea q=1 corespunde alimentarii cu lichid la temperatura de fierbere (i=i'), q>1 daca i<i' (lichid la o temperatura mai mica decât cea de fierbere) si q=0 daca i=i" (alimentare cu vapori saturati). Considerând talerele în regim izoterm (temperatura constanta în timp), ecuatia de bilant termic pentru talerul de alimentare este de forma:

(145)

În aceasta ecuatie se fac substitutiile:

i" = i' + i_vap

i =i"- q i_vap = i' + (1-q) i_vap (dedusa din (144)).

Ecuatia (145) devine:

(146)

Din (146) si (143) se deduce relatia:

(147)

Din aceasta relatie se observa ca:

n=1,2, N

iar în blazul coloanei:

(150)

În acelasi mod se scrie ecuatia de bilant pentru componentul volatil în rezervorul de distilat:

(151)

La ecuatiile de mai sus, se adauga relatii ce decurg din existenta elementelor de reglare a nivelului în blaz si în rezervorul de distilat:

W = f( H_W )    si respectiv D = f( H_D ) (152)

În ipotezele de lucru prezentate, apar 2 N + 5 variabile de timp ale coloanei: x₁, x₂, .x_N, x_D, x_w, y₁.y_N, y_w, V, V', L'. Acestea se calculeaza din cele N+2 ecuatii de bilant al componentului volatil pe talere, în rezervorul de distilat si în blaz, la care se adauga relatiile de tip Fenske (137), în numar de N+1 (din care se calculeaza concentratiile în faza de vapori y₁, y₂.y_N, y_W în functie de concentratiile corespunzatoare în faza lichida) si respectiv relatiile între debite, (147) si (148).

În ecuatiile de mai sus, V' se calculeaza functie de sarcina termica a refierbatorului, H_n rezulta din caracteristicile talerului, debitele W si D se calculeaza din relatiile (152) în care H_W si H_D sunt fixate si pastrate constante prin sisteme de reglare, iar refluxul se fixeaza în raport cu compozitia dorita a distilatului. Sunt presupuse de asemenea cunoscute, debitul de alimentare, compozitia si starea termica ale alimentarii.

Separarea prin rectificare a amestecurilor multicomponente

Pentru un amestec format din n_c componente, pe fiecare din talerele coloanei se pot scrie n_c-1 ecuatii de bilant masic independente, corespunzatoare la n_c-1 substante din amestec. Pentru talerul n al coloanei aceste ecuatii sunt de forma:

(153)

Relatiile între concentratiile din faza de vapori si cele din faza lichida se deduc de asemenea presupunând stabilirea echilibrului termodinamic pe toate elementele coloanei. Pentru amestecurile având comportare ideala, se pot deduce relatii de tip Fenske plecând de la legea Raoult, la fel ca si pentru amestecurile binare:

(154)

(155)

Din (154) si (155) rezulta:

(156)

Pentru amestecurile ce prezinta comportare neideala în faza lichida si ideala în faza de vapori relatiile de echilibru sunt de forma:

(157)

sau (158)

Din (153) si (158) rezulta pentru talerul n:

, j=1, 2,.n_c-1 (159)

Din ecuatia (159) rezulta expresia constantei de timp a variatiei concentratiei componentului j pe talerul n:

(160)

Pentru amestecurile de substante cu volatilitatile foarte diferite, valorile constantelor de timp pot diferi mult de la o substanta la alta, ceea ce conduce adesea la probleme de stabilitate a integrarii numerice. O solutie simplificatoare aplicabila în astfel de situatii este neglijarea constantelor de timp mici (corespunzatoare componentilor cu volatilitati ridicate). Ecuatiile de bilant (159) se particularizeaza pentru acesti componenti sub forma:

(161)

Ipoteza de echilibru termodinamic între fazele lichida si de vapori existente pe talerele coloanei nu este în general acceptabila. O descriere mai apropiata de realitatea fizica este realizabila introducând notiunea de eficienta a talerului sau, si mai exact, tinând seama de cinetica transferului de masa interfazic (lichid - vapori).