Generatorul independent de tensiune

Generatorul independent de tensiune

Generatorul ideal de tensiune este elementul activ de circuit a carui tensiune la borne nu depinde de intensitatea curentului, generatorul fiind caracterizat de variatia in timp a tensiunii electromotoare:

(8.19) .  

In planul () caracteristica de functionare este o dreapta paralela la axa (fig. 8.22). Deoarece intensitatii curentului ii corespunde univoc o valoare a tensiunii, generatorul ideal de tensiune poate fi considerat rezistor neliniar activ cu control de curent. Simbolul sau grafic este acela din figura 8.23.

Generatorul este de tensiune continua daca tensiunea electromotoare este constanta in timp: .

Generatorul real de tensiune continua este caracterizat de tensiunea electromotoare si de rezistenta (fig. 8.24), caracteristica de functionare fiind o dreapta (fig. 8.25) de ecuatie:

(8.20) .  

  Generatorul independent de curent

Generatorul ideal de curent este elementul activ de circuit avand intensitatea curentului independenta de tensiune, ecuatia caracteristica fiind:

(8.21) .  

In planul () caracteristica de functionare este o dreapta paralela la axa (fig. 8.26). Deoarece tensiunii ii corespunde univoc o valoare a intensitatii curentului, generatorul ideal de curent poate fi considerat rezistor neliniar activ cu control de tensiune. Simbolul sau grafic este acela din figura 8.27.

Daca intensitatea curentului este constanta in timp, , generatorul este de curent continuu.

Generatorul real de tensiune continua este caracterizat de injectia de curent si de conductanta (fig. 8.28), caracteristica de functionare fiind:

(8.22)

8.2. Marimi electrice de circuit

Studiul circuitelor linire se face cu ajutorul marimilor intensitate a curentului electric de conductie, densitate a curentului electric de conductie, tensiune electromotoare si tensiune electrica, marimi care sunt numite, in mod obisnuit, marimi electrice de circuit.

8.2.1. Intensitatea curentului de conductie

Asupra conductoarelor aflate in stare electrocinetica se exercita in campul magnetic forte suplimentare in raport cu cele electrice, termomecanice si cu cele magnetice determinate de deplasarea sarcinii odata cu conductorul sau de momentele magnetice ale corpurilor. O portiune rectilinie de lungime (orientata in sensul deplasarii sarcinii pozitive) este supusa in campul magnetic uniform fortei electromagnetice , ale carei intensitate, directie si sens satisfac regula efectuarii produsului . Factorul de proportionalitate este o marime primitiva, globala (integrala), scalara, pozitiva, negativa sau nula, dependenta numai de starea electrocinetica a conductorului, pe care in felul acesta o caracterizeaza. Macroscopic, aceasta marime, numita intensitate a curentului electric de conductie, este definita ca raport dintre forta maxima ce corespunde cazului si produsul modulelor celor doi vectori:

^. (8.23)

Unitatea de masura a intensitatii curentului electric de conductie, amperul [A], este definita ca fiind acea valoare a intensitatii curentului care stabileste intre doua conductoare paralele, situate in vid la distanta de 1m, o forta electrodinamica de 2.10^-7N/m (v. 1.2.1). Unitatea de masura este astfel aleasa incat, sub aspect microscopic, ea sa corespunda unei viteze de deplasare a sarcinii prin sectiunea conductorului de un coulomb pe secunda [1C/s].

8.2.2. Densitatea curentului electric de conductie

Caracterizarea locala a starii electrocinetice se face cu ajutorul marimii numita densitate a curentului electric de conductie. Ea este definita ca intensitate pe unitatea de arie perpendiculara pe directia deplasarii sarcinilor, a unei suprafete ce se strange in jurul punctului considerat (fig. 8.29): [A/m²]. Atribuind densitatii curentului de conductie directia si sensul deplasarii sarcinilor o definim ca fiind marimea vectoriala al carei flux printr-o suprafata este egal cu intensitatea curentului prin acea suprafata (v. 1.2.1):

(8.24)

 

In calculele tehnice de dimensionare ale conductoarelor circuitelor electrice se admite ipoteza conductorului filiform, ori de cate ori dimensiunile sectiunii sunt mici in raport cu lungimea conductorului. Aceasta revine la a considera densitatea de curent uniform repartizata in sectiune iar vectorul densitate de curent omoparalel cu tangenta la axa conductorului. Daca sectiunea conductorului este constanta, relatia (8.25) devine:

(8.26) ,  

adica:

(8.27)  

Relatia (8.27) este folosita pentru a verifica daca densitea de curent in conductor ramane in limita admisa.

8.2.3. Tensiunea electromotoare

Starea electrocinetica a conductoarelor este consecinta a deplasarii purtatorilor de sarcina in conductor atunci cand nu mai este indeplinita conditia de echilibru electrostatic ().

Marimea valoric egala cu lucrul mecanic efectuat de fortele electrice si neelectrice pentru a deplasa sarcina pozitiva de un coulomb de-a lungul unui contur inchis se numeste tensiune electromotoare de contur. Ea este modelata de circulatia campului electric rezultant de-a lungul conturului:

(8.28) .

Prima integrala din membrul al doilea exprima tensiunea electrica de-a lungul conturului , iar cealalta, tensiunea electromotoare imprimata. T.e.m. imprimata caracterizeaza sursele cu camp electric imprimat, exprimand capabilitatea fortelor neelectrice de a efectua lucru mecanic pentru transportul sarcinii (v. subcap 4.3).

In cazul unui regim electrocinetic stationar transportul sarcinilor se realizeaza numai pe contururi inchise. In acest caz tensiunea electromotoare de contur provine numai din tensiunea electromotoare imprimata deoarece , conform teoremei potentialului electric stationar, regimul electrocinetic stationar fiind intretinut, asa cum s-a aratat in capitolul 4, numai de cauze neelectrice. El se realizeaza pe seama consumului de energie neelectrica acumulate in campurile imprimate asa cum se intampla, de exemplu, in sursele chimice, unde fortele neelectrice efectueaza lucru mecanic pentru transportul sarcinilor pe seama consumului energiei unor reactii chimice.

In regim electrocinetic nestationar intensitatea campului electric are o componenta potentiala - , numita si camp electric coulombian si una rotationala - , produsa prin inductie electromagnetica, numita si camp electric indus: . In acest caz, tensiunea electromotoare de contur va fi produsa de campul electric indus si de campul electric imprimat, fiind egala cu suma dintre t.e.m. indusa si t.e.m. imprimata:

.   (8.29)

Prin tensiune electromotoare intre doua puncte ale unei curbe deschise se intelege circulatia sumei campului electric indus si a campului electric imprimat, efectuata intre cele doua puncte:

  (8.30)

Din cele expuse, rezulta ca t.e.m. este o marime scalara, cu valoare pozitiva sau negativa in functie de sensul ales pentru integrare. Sensul ales pentru integrare va fi sensul de referinta pentru care valoarea rezultata prin integrare va fi pozitiva (v. si §. 2.5).

Evident, unitatea de masura pentru t.e.m. este voltul [V].

8.2.4. Tensiunea electrica

Tensiunea electrica exprima capabilitatea fortelor campului electric rezultant de a efectua lucru mecanic pentru transportul sarcinii de-a lungul unei curbe, intre doua puncte ale acesteia, modelul sau fiind:

.   (8.31)

Tensiunea la borne a unui dipol, , are ca model circulatia campului electric rezultant pe o curba deschisa, , prin dielectricul ce separa bornele a si b, iar tensiunea in lungul firului, , este definita de circulatia campului electric coulombian pe curba deschisa dusa prin conductor intre cele doua borne (fig. 8.30):

(8.32)

respectiv:

.   (8.33)

In regim electrocinetic nestationar cele doua tensiuni sunt diferite, . In schimb, in regimul electrocinetic stationar () rezulta:

,   (8.34)

deoarece circulatia vectorului nu depinde de drum, asa ca .

Ca si tensiunea electromotoare, prezentata in paragraful anterior, tensiunea electrica este o marime scalara afectata de semnul plus sau minus dependente de sensul de integrare in raport cu sensul de referinta. Sensul de referinta este acela care da o valoare pozitiva tensiunii si care se indica printr-o sageata sau un arc orientat unind cele doua borne.

8.2.5. Asocierea sensurilor de referinta

Caracterul algebric al unor marimi scalare de circuit, rezultat din definitia lor in care intervin elemente geometrice (de arie si de curba) orientate, susceptibile de valori pozitive, nule sau negative impune alegerea unor sensuri de referinta pentru calculul lor precum si stabilirea unor conventii de asociere a acestor sensuri de referinta, pentru cazurile in care intervin, in aceeasi relatie, mai multe asemenea marimi. In absenta unor reguli unice de asociere a sensurilor de referimta, evident, scrierea ecuatiilor si concluziile asupra solutiilor sunt susceptibile de interpretari si chiar de erori.

Din acest motiv, pentru scrierea legilor electromagnetismului se stabilesc reguli care se transmit si teoremelor deduse din aceste legi. Ele au fost expuse cu ocazia prezentarii legilor teoriei macroscopice a campului electromagnetic in subcapitolul 1.3. In cele ce urmeaza se reiau cateva din ele, cu referire la scrierea corecta a ecuatiilor circuitelor electrice:

i) in legile in care intervin fluxuri conservative prin sectiunile transversale ale unor tuburi de linii de camp si circulatii in lungul unor curbe , in general deschise, sensul de referinta al fluxului se ia acelasi cu sensul de referinta al circulatiei ‑ (fig. 8.31).

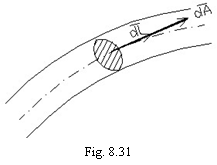Aceasta regula este folosita si la scrierea sub forma integrala a legii lui Ohm, unde sensul de referinta al tensiunii de-a lungul firului, , respectiv al t.e.m., se asociaza cu sensul de referinta al curentului, :

(8.35) sau .

S-a considerat aria sectiunii aceeasi in lungul tubului.

Aceasta regula se va aplica, evident, si la scrierea teoremei a II-a a lui Kirchhoff care este o consecinta a legii lui Ohm;

ii) in legile in care intervin fluxuri prin suprafete inchise , se alege ca sens de referinta sensul determinat de normalele exterioare ale suprafetei. Astfel, la scrierea legii conservarii sarcinii, asociind sensul de referinta al curentului cu semnul pozitiv al sarcinii electrice din interiorul suprafetei (fig. 8.32), rezulta:

(8.36) sau

Aplicand aceasta regula la scrierea teoremei I a lui Kirchhoff, consecinta a legii conservarii sarcinii, se stabileste ca sens de referinta al curentului sensul normalei exterioare la suprafata imaginara ce inconjoara nodul (fig. 8.33) ;

iii) In scrierea teoremelor ce intervin in calculul circuitelor se intalneste adesea tensiunea la borne, modelata printr-o integrala de linie referitoare la curbe deschise, situate intre doua borne, A si B (fig. 8.34).

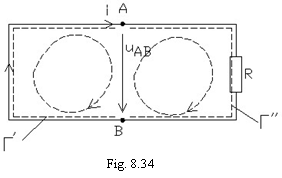La scrierea relatiilor pentru circuite ca acela din figura 8.34 este necesara asocierea sensurilor pentru diferitele marimi electrice in acelasi mod in care s-a facut aceasta asociere la enuntarea legilor. Acolo unde sensurile de referinta a doua marimi sunt independente intre ele, trebuie sa se prezinte in mod explicit conventia folosita pentru scrierea relatiilor dintre aceste marimi.

La scrierea legii lui Ohm, curentul si tensiunea electromotoare s-au asociat cu acelasi sens de referinta iar curentul si tensiunea de-a lungul firului s-au asociat de asemenea cu acelasi sens de referinta.

Tensiunea la borne nu depinde de drumul de integrare. Ea poate fi calculata intre cele doua borne ale circuitului pe oricare portiuni de contururi cuprinse intre bornele A si B ce trec prin conductor sau prin exterior.

Integrand pe conturul in sensul curentului, adica de la borna B catre borna A, rezulta:

(8.37)

Integrand pe conturul , tot in sensul curentului, se obtine:

(8.38)

Asa dar, sensul pozitiv al tensiunii la bornele A si B ar depinde, in fond, de sensul in care integram pe un contur ce trece prin cele doua borne, urmand sa precizam acest lucru, in mod explicit, printr-o sageata.

Pentru a se realiza insa o unitate in ceea ce priveste modul de scriere a ecuatiilor circuitului se adopta urmatoarele conventii de atribuire a sensului pozitiv pentru tensiunea la borne:

- regula de generator (sursa): Tensiunea la bornele sursei este pozitiva in sensul de la A la B, daca curentul prin sursa are sensul dinspre borna B catre borna A;

- regula de la receptor : Tensiunea la bornele receptorului este pozitiva in sensul de la A la B, atunci cand curentul prin receptor are sensul tot de la borna A catre borna B.

Prin atribuirea sensului pozitiv al tensiunii la borne in circuitul din figura 8.34. dupa cele doua reguli, ecuatia legii lui Ohm pe ramura sursei se va scrie:

,   (8.39)

iar pe ramura receptorului:

. (8.40)

Scriind acum ecuatiile bilanturilor de puteri: si respectiv se constata ca regula de la receptor si regula de la generator au urmarit atribuirea sensului pozitiv al tensiunii la borne, astfel incat puterea vehiculata prin borne sa fie pozitiva atunci cand este efectiv cedata la generator si primita de receptor.

Valoarea practica a regulilor de asociere a tensiunilor se poate aprecia integral in cazul circuitelor de curent alternativ, asa cum se va vedea in subcapitolul 8.5.

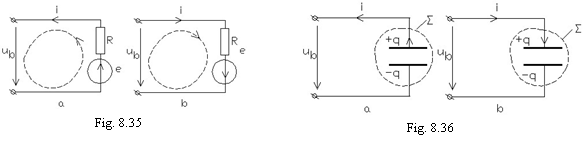
In figura 8.35 se exemplifica modul in care se aplica aceste reguli la scrierea ecuatiilor unui dipol, de unde se poate vedea ca pentru studiul dipolului regula adoptata este indiferenta, dar rezultatele calculelor trebuie interpretate in raport cu sensurile de referinta alese;

iu) in cazul condensatoarelor, regulile uzuale de asociere a sensurilor de referinta sunt cele utilizate la formularea legii conservarii sarcinii. In figurile 8.36 a si b sunt indicate aceste sensuri de referinta, iar ecuatiile corespunzatoare sunt:

(8.41) cu ^,  

respectiv:

(8.42) cu  

ui) in cazul bobinelor, regulile care asociaza sensurile de referinta pentru fluxuri si curentii care le produc rezulta din legea circuitului magnetic in care, sensului de referinta al fluxului ii este asociat sensul de referinta al curentilor dupa regula burghiului drept, toate inductivitatile fiind pozitive. In teoremele lui Maxwell pentru inductivitati:

(8.43) ,  

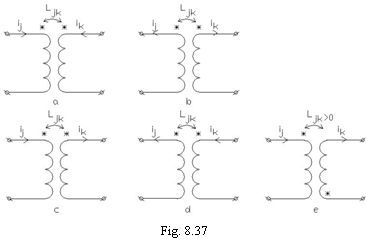inductivitatea mutuala fiind pozitiva sau negativa, este insa necesar sa se indice sensurile de referinta pentru circuitele cuplate prin (fig. 8.37) cu ajutorul asteriscurilor care indica bornele considerate de inceput ale bobinei (in sensul de bobinare). In functie de acestea, inductivitatea se considera pozitiva daca ambii curenti intra sau ies prin bornele marcate si negativa daca cei doi curenti ies diferit in raport cu bornele respective.

Potrivit celor de mai sus, fluxul mutual din circuitul produs de curentul va fi pentru circuitele a si b, respectiv pentru circuitele c si d.

Figura 8.37e sugereaza ca bobinele au sensuri de bobinare diferite si in raport cu sensurile asociate curentilor se va lua ;

uii) marimile care nu respecta regulile de asociere a sensurilor de referinta se introduc in ecuatii cu semn schimbat. Daca din calcule rezulta valori negative, marimile respective au sensul contrar celui de referinta.