IMPEDANTA CARACTERISTICA SI CONSTANTA DE PROPAGARE A CUADRIPOLULUI SIMETRI

IMPEDANTA CARACTERISTICA SI CONSTANTA DE PROPAGARE A CUADRIPOLULUI SIMETRI

    (22)

rezolvand ecuatia (22) se obtine impedanta caracteristica a cuadripolului simetric sub forma :

    (23)

Aiasta expresie a impedantei caracteristice permite sa tragem concluzia ca in cazul particular cand

B = C =0 (24)

orice impedanta este o impedanta caracteristica .

Din expresiile care dau constantele cuadripolului pentru cele doua scheme echivalente :

B = 2Z₁ + Z₁² Y₀ ; C = Y₀, pentru schema in T (25)

B = Z₀ ; C = 2Y₁ + Y₁² Z₀, pentru schema in II, (26)

conditia (24) conduce la urmatoarele conditii echivalente : Y₀ = 0    si Z₁ = 0, respectiv Z₀ = 0 si Y₁ = 0, adica aceste conditii pot fi indeplinite numai pentru cuadripoli formati exclusiv din elemente reactive acordate la rezonanta (fig.5) .

Daca cuadripolul simetric este inchis pe impedanta caracteristica,ecuatiile cuadripolului se scriu :

U = A U₂ + B I₂ = U₂ ( A +     (27)

I = C U₂ + A I₂ = I₂ (A +     (28)

Deci :

(29)

Se numeste constanta de propagare a cuadripolului simetric logaritmul natural al expresiei (29) :

Aplicatie

Sa se determine constantele fundamentale ale cuadripolului din figura 18.6, precum si impedanta caracteristica si constanta de propagare , daca la o frecventa data, schema echivalenta in T contine elemente indicate pe figura in ohmi .

Constantele fundamentale se determina cu relatiile (8) :

(43)

(44)

    (45)

Impedanta caracteristica (relatia 23) este :

(46)

Constanta de propagare este :

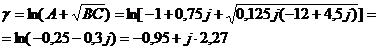(47)