implementarea functiilor binare cu retele de porti
1. scopul lucrarii
In aceasta lucrare se face pentru inceput, o prezentare teoretica a principalelor etape ce trebuie urmarite in procesul de implementare a functiilor logice dupa care, se trateaza unele aspecte ce apar in practica datorita comportamentului real al portilor logice.
2. CONSIDERENTE TEORETICE
2. 1. Clasificarea circuitelor logice
In functie de relatia de legatura existenta intre semnalele de intrare si cele de iesire, relatie descrisa de catre functia de transfer, circuitele logice se impart in: circuite logice combinationale (CLC) si circuite logice secventiale.
Circuitele logice combinationale reprezinta clasa circu 454i82e itelor logice pentru care starea iesirilor este, in fiecare moment de timp, complet detrminata numai de starea logica a intrarilor. Pentru CLC-uri nu exista o dependenta a iesirilor fata de starile anterioare prin care a trecut circuitul. Din acest motiv structura interna nu necesita prezenta elementelor de memorare. Analiza pur logica a acestor circuite se face fara intoducerea variabilei timp.
Circuitele logice secventiale reprezinta clasa circu 454i82e itelor logice pentru care exista cel putin un moment de timp in care iesirile sunt determinate atat de stsrea prezenta a intrarilor cat si de o stare anterioara prin care a trecut circuitul. Privind lucrurile dintr-o alta perspectiva putem spune ca starea prezenta a circuitului secvential poate influienta, chiar si dupa disparitia sa, evolutia viitoare a circuitului. Structura circuitelor secventiale contine, in mod obligatoriu, elemente de memorare deoarece, numai prin memorare efectul unei stari prezente se poate extinde si in viitor.
Analiza circuitelor secventiale necesita introducerea variabilei timp insa, aceasta este privita ca o succesiune discreta de momente (t1,t2, ,ti, ). Un circuit secventia se poate descompune intr-un circuit pur combinational si o zona de memorie. Aceasta divizare permite o abordare mai usoara a acestor structuri.
2. 1. Functia de transfer a unui CLC. Functii binare.
Pentru cazul general, al unui CLC cu n intrari si m iesiri, starea semnalelor de intrare este specificata printr-un vector cu n componente X(x1, x2, , xn) iar starea iesirilor de un vector cu m
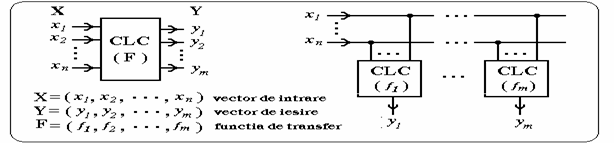
Fig. 1. Schema bloc a unui circuit logic combinational
componente Y(y1, y2, , ym). Relatia de legatura dintre intrare si iesire este descrisa de catre functia de transfer F(f1, f2, , fm). In cazul particular in care m=1, functia de transfer are o singura componenta si este denumita functie binara. Studiul functiilor binare prezinta o importanta deosebita deoarece, conform reprezentarii din fig. 1, un CLC cu m iesiri poate fi descompus intr-o suma de m functii binare.
2. 2. Reprezentari ale functiei de transfer ale unui CLC
Functia de transfer a unui CLC poate fi descrisa in mai multe moduri dintre care cele mai utilizate sunt: tabelul de adevar, forma canonica conjuctiva sau disjunctiva, diagrama Veitch-Karnaugh, forma analitica redusa, descrierea in limbaj natural, etc.
Tabelul de adevar complet defineste functionarea unui sistem logic prin listarea valorilor de iesire pentru fiecare combinatie a variabilelor de intrare (vector de intrare). Pentru cazul general al unui CLC cu n intrari si m iesiri tabelul de adevar va contine 2 la puterea n linii (ceea ce reprezinta numaruul maxim al combinatiilor ce se pot obtine cu variabilele de intrare) si n+m coloane (cate una pentru fiecare variabila de intrare si respectiv, componenta a functiei de transfer).
Spre exemplu, in fig. 2, se prezinta tabelul de adevar complet pentru un CLC caracterizat de 3 intrari si 2 iesiri. Pentru acest caz, numarul de linii ale tabelului de adevar este 8 iar numarul de coloane 5. Tot aici se prezinta modul de descompunere a functiei de transfer in cele doua functii binare ce o alcatuiesc.

Fig. 2 Tabelul de adevar complet al unui un CLC cu 3 intrari si 2 iesiri
Tabelele de adevar ale unor functii binare de mai multe variabile devin ample atunci cand numarul variabilelor de intrare creste. Pentru a simplifica scrierea, se utilizeaza tabelul de adevar redus, in care se trec numai combinattiile de intrare pentru care functia are aceeasi valoare logica. Apar astfel doua forme ale tabelului redus: una pentru valorile "adevarat" si alta pentru valorile "fals" ale functiei. Deci, una pentu valorile de " 1" iar cealalta pentru valorile de "0" ale functiei. Modul de trecere de la o forma la alta este ilustrat in fig. 3.
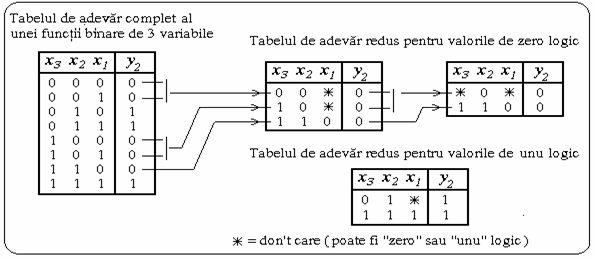
Fig. 3. Trecerea de la forma completa la formele reduse ale tabelelor de adevar
Forma canonica constituie o alta modalitate de reprezentare a functiilor binare in care, descrierea functionarii se face analitic. Scrierea canonica a unei functii binare se poate face in doua moduri:
prin utilizarea unei sume a tuturor mintermenilor pentru care functia binara prezinta valoarea "1" - cazul primei forme canonice, denumita si forma canonica disjunctiva;
prin utilizarea unui produs al tuturor maxtermenilor pentru care functia binara prezinta valoarea "0"- cazul celei de-a doua forme canonice denumita si forma canonica conjunctiva.
Definitii:
Mintermenul este un produs logic la care participa fiecare variabila de intrare o singura data: sub forma directa - daca variabila de intrare este unu logic, sau sub forma complementata - daca variabila de intrare este zero logic.
Maxtermenul este o suma logica, un produal, la care participa fiecare variabila de intrare luata o singura data: sub forma directa - daca variabila de intrare este zero logic, sau sub forma complementata - daca variabila de intrare este unu logic.
Exemplu Pentru functia de transfer prezentata in figura 2 obtinem:
Modul de definire al min / max - termenilor se prezinta in tabelul de mai jos:
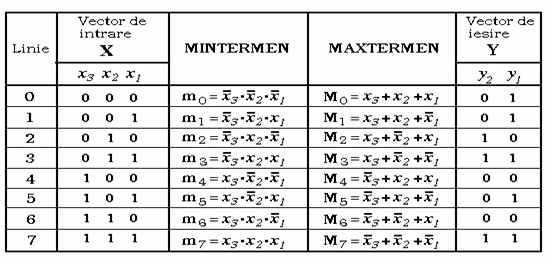
Prima forma canonica (forma disjunctiva) a celor doua functii binare:


A doua forma canonica (forma conjunctiva) a celor doua functii binare:


Observatii:
Se remarca faptul ca atat mintermenii, cat si maxtermenii, sunt dependenti numai de starea logica a varibilelor de intrare si nu depind de valorile de iesire ale functiei logice.
Din analiza expresiilor celor doua forme canonice se observa ca, desi descriu aceleasi functie logica, cu cat o forma canonica este mai restransa cu atat cealalta este mai ampla.
In practica se recomanda utilizarea primei forme canonice pentru functiile binare care au un numar mai redus de valori "adevarat", printre valorile functiei, si a formei a doua in caz contrar.
Pentru exemplul considerat, se obtin expresii mai simple daca se utilizeaza prima forma canonica pentru y2, respectiv cea de-a doua forma pentru y1.
Forma redusa este o expresie analitica ce rezuta in urma simplificarilor efectuate, de regula, asupra formelor canonice. Procesul de simplificare are drept scop reducerea numarului de simboluri utilizate, si reducerea la minim a expresiilor ce descriu o functe binara.
Simplificarea functiilor binare este posibila datorita existentei termenilor redundanti ce apar de cele mai multe ori in formele canonice. Un termen redundant este acela care, prin intoducerea sau suprimare sa, nu afecteaza valorile logice de iesire ale functiei binare. Metodele de simplificare apar drept consecinte demonstrabile ale proprietatilor algebrei binare. Ca metode de simplificare amintim: metoda factorului comun, metoda adiacentelor, metoda transpozitiei, metoda consensului, setc.
Fiecare metoda exploateaza, de cele mai multe ori, doar una din proprietatile algebrei binare t motiv pentru care, o simplificare eficienta, maximala, nu se poate obtine decat prin aplicarea succesiva a mai multor metode sau prin combinarea acestora.
2. 3. Simplificarea functiilor binare folosind digramele Veitch-Karnough
In aceasta lucrare se prezenta o metoda de simplificare des uzitata, bazata pe proprietatea de adiacenta, cunoscuta sub denumirea de diagrama Veitch-Karnough. Diagramele Veitch-Karnough reprezinta de fapt tabele de adevar modificate astfel incat sa permita gruparea cu usurinta, pe cale grafica, a termenilor adiacenti. In fig. 4 se prezinta cele doua tipuri de diagrame pentru 2 si respectiv 3 variabile de intrare.
Definitie:
Doi termeni sunt adiacenti daca
trecerea de la unul la celalalt se face prin complementarea unei singure
variabile. Exemplu de termeni adiacenti: ![]() .
.
CONSTRUCTIA DIAGRAMEI:
Se traseaza o diagrama cu dimensiuni in concordanta cu numarul variabilelor de intrare.
Se face alocarea arbitrara a variabilelor de intrare pe linii, respectiv pe coloane.
Se codeaza liniile si coloanele astfel incat trecerea de la o linie la alta, sau de la o coloana la alta, sa se faca prin modificarea unei singure variabile. De regula, numerotarea se face in cod Gray de sus in jos pentru linii si de la stanga la dreapta pentru coloane.
Se completeaza celulele diagramei cu valorile corespunzatoare ale functiei binare.

Fig. 4. Exemple de diagrame Veitch -Karnaugh
TRASAREA SUPRAFETELOR:
Se decide asupra formei canonice ce va fi utilizata (prima forma canonica daca in diagrama sunt mai putine valori "1" decat "0", altfel forma a doua). In continuare, presupunem cazul implementarii dupa "unu logic" deci, prima forma canonica.
Se traseaza suprafete patrate sau dreptunghiulare, de arie cat mai mare posibila, alcatuite din 1, 2, 4, 8, 16, celule in care valoarea functiei este aceeasi (in cazul considerat "1").
Este necesar ca fiecare valoare de "1" sa fie cuprinsa in cel putin o suprafata.
Trasarea suprafetelor trebuie facuta astfel incat numarul acestora sa fie cat mai mic iar aria acestora cat mai mare;
Valorile don't care ale functiei logice se trec in diagrama ca o steluta si poat fi cuprinse in orice suprafata (fie de "0", fie de "1") daca, in acest mod, aria respectivei suprafete creste.
In trasarea zonelor se are in vedere faptul ca marginea din stanga a diagramei este vazuta ca o continuare a celei din dreapta, iar marginea de sus ca o continuare a celei de jos. Deci, trebuie sa percepeti diagrama ca si cum ar fi desenata pe o sfera.
EXTRAGEREA EXPRESIEI ANALITICE REDUSE A FUNCTIEI LOGICE:
a) Pentru cazul "implementarii dupa unu logic" se procedeaza astfel:
- pentru fiecare suprafata trasata se scrie un produs format din variabilele ce raman constante in interiorul respectivei suprafete;
- expresia finala a functiei binare se obtine prin sumarea produselor de la punctul anterior;
- regula de scriere a variabilelor este cea utilizata pentru mintermeni.
b) Pentru cazul "implementarii dupa zero logic" se procedeaza astfel:
- pentru fiecare suprafata trasata se scrie o suma alcatuita din variabilele ce raman constante in interiorul respectivei suprafete;
- expresia finala a functiei binare se obtine realizand un produs logic al sumelor de la punctul anterior;
- regula de scriere a variabilelor este cea utilizata pentru maxtermeni.
Exemplu: In fig. 5 se prezinta modul de utilizare a diagramelor Karnaugh in simplificarea functiilor binare date prin tabelul de adevar din fig. 2.
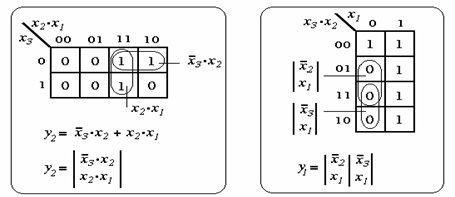
Fig. 5. Diagramele Karnaugh pentru functiile y2, y1
Observatii:
Repartitia variabilelor pe linii, respectiv coloane se face arbitrar.
Simplificarea functiilor prin metoda diagramelor Veitch - Karnaugh nu conduce, de regula, la expresii minimale deoarece nu se ia in calcul decat proprietatea de adiacenta.
Pentru exemplul considerat se vede posibilitatea de a continua simplificarea expresiilor prin metoda factorului comun.
Se obtine in final:
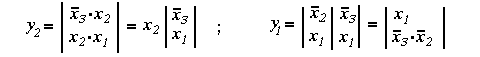
2. 4. Sinteza functiilor binare folosind retele de porti logice
In primul rand, trebuie precizat ca, in practica, exista mai multe variante de realizare ale aceleasi functii logice. Spre exemplu, daca in procesul de sinteza se pleaca de la prima forma canonica vom avea nevoie de: inversoare pentru complementarea variabilelor de intrare, porti AND pentru calculul mintermenilor si o poarta OR pentru realizarea sumei de mintermeni. Un astfel de caz este prezentat in figura 5. a)
. 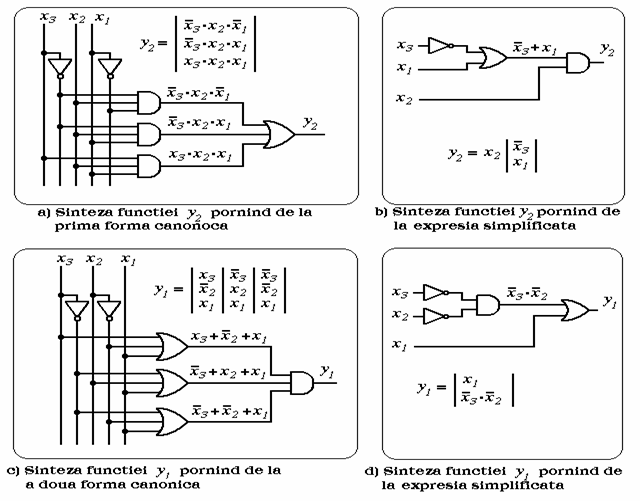
Fig.5 Exemple de sinteza a functiilor logice y2, y1
In practica, sinteza functiilor binare pornind de la formele canonice, se utilizeaza mai rar, deoarece, conduce la retele complicate de porti logice. Retele mai simple se obtin daca procesul de sinteza se incepe de la o expresie cat mai redusa a functiei binare. Analizand schemele din figura 5, se observa diferente semnificative intre implementarile inainte si cele de dupa simplificare.
Asa dupa cum se stie, sistemele de operatori: (AND, NOT), (OR, NOT), (NOR), (NAND) sunt sisteme complete de operatori - ceea ce inseamna ca pot fi utilizate in descrierea oricarei functii binare. Interes practic mai mare prezinta ultimele duoa deoarece, ne indica posibilitatea, de a implementa orice functie logica cu ajutorul unui singur tip de poarta, fie NAND fie NOR.
Transpunerea unei scheme logice oarecare intr-o logica de acelasi tip se face, utilizand in mod convenabil, urmatoarele reguli:
R1: La iesirea unui etaj logic se poate introduce un cerculet de negare daca, corespunzator, la intrarea nivelului logic urmator se face acelasi lucru (" dubla negare este adevar").
R2: Introducerea la o iesire a unui cerculet de negare trebuie urmata de adaugarea unui inversor. Introducerea la o intrare a unui cerculet de negatie trebuie precedata de negarea respectivei variabile de intrare.
R3: Trecerea de la o poarta la alta se face conform echivalentelor de mai jos:
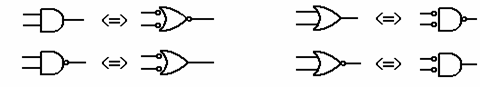
In functie de schema logica initiala rezultatul transpunerii in logica de acelasi tip, poate conduce spre scheme mai simple sau, dimpotriva, mai complicate decat schema initiala. Cateva transpuneri in logica de acelasi tip sunt exemplificate in figura 6.
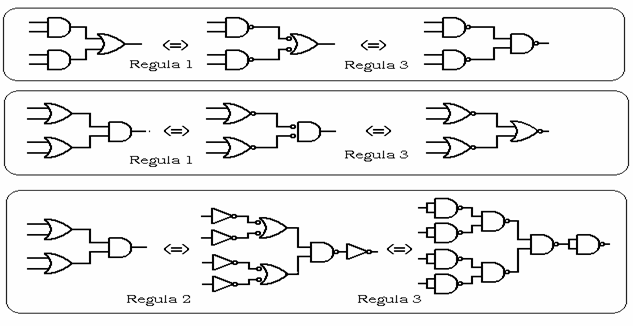
Fig. 6. Transpunerea unor scheme logice in logica de acelasi tip
Pentru situatiile in care logica de acelasi tip nu se impune in mod strict, aplicarea regulilor R1, R2, R3, pe portiuni convenabile ale schemei, poate sa determine reducerea necesarului de porti al schemei. De exemplu, aplicarea regulii R3 pentru functia y2, are ca efect reducerea necesarul de porti de la 4 la 2 si, in plus, implementarea se face folosind doua tipuri de porti fata de trei cat era initial. Aceasta situatie este prezentata in figura 7.

Fig. 7. Reducerea numarului de porti folosind echivalenta dintre acestea
2. 5. Efecte ale timpului de propagare in functionarea CLC-urilor
Consideratiile de pana acum, despre implementarea functiilor binare, au fost facute in ipoteza comportamentului ideal al portilor logice. Din nefericire, portile de care dispunem in prezent sunt inca departe de cele ideale. O serie de parametrii ai portilor reale (timp de propagare, factor de incarcare, nivele de tensiune, etc. ) au efecte nedorite in functionarii CLC-urilor. O atentie deosebita trebuie acordata efectelor datorate timpului de propagare.
Timpul de propagare reprezinta decalajul care se inregistreaza intre momentul aplicarii unui semnal logic la intrarea unui circuit si momentul aparitiei raspunsului la iesirea acestuia.
Timpul de propagare printr-o poarta logica este dependent de o serie cauze printre care cele mai semnificative sunt:
Tehnologia de realizare;
Factorul de incarcare al iesirii (numarul portilor comandate de respectiva iesire);
Capacitatea echivalenta, formata din capacitatile de intrare ale portilor comandate, sesizata de iesire ;
Starea logica in care se afla iesirea. De regula tpHL, timpul de propagare pentru cazul in care iesirea comuta din starea HIGH in starea LOW, este mai mic decat tpLH.
Timpul de propagare printr-un circuit logic este dependent de numarul de niveluri logice (porti)conectate intre intrare si iesire. Pentru evaluarea si compararea timpilor de propagare se introduce notiunea de adancime a circuitului notata cu D a carei valoare este egala cu mumarul maxim de niveluri conectate intre intrarea si iesirea circuitului.
Inegalitatea timpilor de propagare pentru cele doua stari logice are ca efect:
Reducerea duratei de unu logic a impulsurilor ce parcurg porti neinversoare conectate in serie. Daca numarul portilor din lant este mare, iar durata de unu logic a impulsurilor este redusa exista riscul ca acestea sa se piarda dupa un numar oarecare de porti.
Pastrarea aproape nealterata a duratei de unu logic a impulsurilor in cazul in care lantul de porti este format din porti inversoare. Pentru aceste cazuri exista o tendinta de regenerare a uratei initiale a impulsului dupa fiecare doua porti.
Avand in vedere aspectele prezentate mai sus se recomanda ca CLC-urile sa fie astfel implementate incat sa prezinte o adancime minima iar portile sa fie inversoare. Din aceste motive porta de baza a fiecarei familii de circuite logice este o poarta inversoare: NAND pentru familia TTL respectiv NOR pentru CMOS.
Hazardul combinational, denumit si hazard logic, se manifesta prin aparitia unor semnale parazite (impulsuri de foarte scurta durata) in perioadele tranzitorii de functionare. Aceste fenomene nu pot fi puse in evidenta numai prin analiza pur logica a circuitelor deoarece in algebra booleana nu intervine marimea timp.
Fenomenele de hazard au urmatoarele cauze:
Asincronismul in comutarea variabilelor de intrare. In analiza booleana se considera ca toate variabilele de intrare comuta in acelasi timp dar in practica acest lucru este aproape imposibil de obtinut. Astfel ca decalajele infime ce exista intre variabilele de intrare obliga circuitul sa treaca prin stari intermediare.
Intarzieri diferite pe traseele de propagare a semnalelor. Chiar daca semnalele de intrare ar fi perfect sincrone, propagarea lor printr-un numar egal de porti dar pe trasee diferite se va face intotdeauna cu intarzieri diferite. In ultima instanta, pentru poarta care prelucreaza semnale ce parcurg trasee diferite, este vorba tot de un asincronism.
Panta limitata a semnalelor electrice. In practica semnalul perfect dreptunghiular este aproximat cu unul trapezoidal pentru care trecerea dintr-o stare logica in alta se face intr-un timp nenul.
Fenomenele de hazard se pot pune in evidenta pe diagramele Veitch-Karnaugh. Aparitia hazardului se produce daca, la comutarea oricarei variabile de intrare, functia logica face un salt dintr-o suprafata avand o valoare logica intr-o alta suprafata cu aceasi valoare logica. Hazardul nu apare daca functia ramane in cadrul aceleasi suprafete sau comuta intr-o suprafata complementara.

Fig. 8. Exemplu de eliminare a hazardului datorat comutarii variabilei a
In fig. 8 se prezinta cazul unei functii binare pentru care comutarea variabilei a este generatoare de hazard in conditiile in care celelalte variabile sunt unu logic. Eliminarea acestei sitatii se poate face prin introducerea unei suprafete suplimentare (cea hasurata), suprafata care are rolul de a unifica cele doua suprafete intre care se facea saltul. In noua situatie, comutarea variabilei a nu mai produce hazard deoarece se ramane in cadrul aceleasi suprafete. Se observa ca noua implementare este mai scumpa.
Hazardul nu deranjeaza intotdeauna si din acest motiv nu este necesar sa luptam impotriva lui fara discernamant, ci numai acolo unde intr-adevar are efecte nedorite sau chiar dezastruase (exemple: intrarea de ceas a unui bistabil sau a unui numarator, intarea de scriere intr-o memorie dar numai atunci cand aceasta este activata etc.).
D E S F A S U R A R E A L U C R A R I I
3.1. Minimizarea functiilor logice
Se considera functia: F= m1+ m7 + m8 + m9 + m14 cu termenii redundanti: m3, m4, m10, m15.
Se cere: a) minimizarea functiei cu ajutorul diagramei Karnaugh;
b) sinteza functiei cu un numar minim de porti NAND cu doua intrari;
3. 2. Oscilatorul in inel
Considerand ca initial in punctul A apare un salt logic de la zero la unu sa se determine semnalele in punctele B, C, D, E, pentru urmatoarele situatii:
a) cazul ideal (timp de propagare nul);
b) cazul real (timp de propagare diferit de zero);

Pe macheta de test realizati o schema similara cu cea de sus dar, pentru ca efectul sa fie mai vizibil, introduceti in bucla 5 inversoare. Vizualizati cu osciloscopul semnalul din punctul E.
Intrebari:
1. Cum explicati aparitia oscilatiilor?
2. Ce se intampla daca in bucla introduceti un numar par (de exemplu 4) inversoare? Verificati raspunsul pe macheta de test.
3. Cum se poate reduce frecventa de oscilatie pentru aceste scheme?
3. 3. Utilizarea timpului de propagare in semnalizarea fronturilor
Pentru schema de mai jos se aplica la intrarea A un semnal digital avand durata de "1" egala cu cea de "0". Analizati formele de unda in punctele B, C, D, E pentru:
a) cazul ideal (timp de propagare nul);
b) cazul real (timp de propagare diferit de zero);
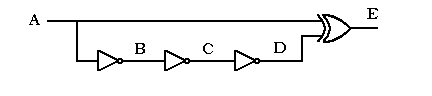
Inlocuiti poarta XOR cu o poarta OR apoi cu o poarta NAND, refaceti subpunctele a) si b) dupa care verificati rezultatele pe macheta de test. Pentru fiecare caz desenati corelat in timp semnalele vizualizate cu ajutorul osciloscopului cu doua canale in punctele A si E.
Intrebari:
1. Ce impulsuri genereaza schemele anterioare si ce fronturi semnalizeaza ?
2. Exista deosebiri intare formele de unda determinate la subpunctul b) si cele obtinute experimental? Cum explicatii acest lucru?
3. Concepeti scheme care sa semnalizeze prin pulsuri pozitive tranzitiile: pozitive, negative sau ambele tranzitii.
3. 5. Hazardul combinational
Pentru schema logica de mai jos conectati la intrarea a un semnal digital periodic cu frecventa de cca. 1MHz, iar intrarile b si c la unu logic. Pentru ca efectul sa fie mai accentuat puteti inlocui inversorul din schema cu un lant de trei inversoare inseriate. Reaalizati mai intai schema desenata cu linie continua, caz in care cea de-a treia intrare a NAND-ului se conecteaza la unu logic, dupa care realizati schema completa (inclusiv partea punctata).

Urmariti functionarea schemei cu ajutorul osciloscopului cu doua spoturi. Desenati corelat in timp formele de unda de la intarea a si de la iesire.
Daca efectul nu este vizibil in locul inversorului conectati uun lant de trei inversoare inseriate
Intrebari:
1. Care este expresia analitica a functiei realizate de schema anterioara ?
2. Ce rol are poarta conectata cu trasu punctat ?
3. 6. Implementarea unui CLC
In ultima parte a lucrarii realizati cu un hard minimal (numar cat mai redus de porti) un CLC care la intrare sa primeasca numerele binare intre 0000 si 1001, iar la iesire sa genereze semnalele necesare afisarii numarului zecimal pe un aranjament de 7 diode electroluminescente (LED-uri). Un astfel de CLC poara denumirea de decodor BCD/7segmente. Modul de notare a LED-urilor ce alcatuiesc un digit este prezntat in figura urmatoare. Semnalele de iesire se considera active pe zero logic (LED aprins daca iesirea este in zero logic).
Se cere implementarea acestui CLC in doua cazuri:
a) decodorul raspunde la coduri pana la 9 inclusiv, dupa care toate segmentele sunt stinse (primul rand de caractere din reprezentarea de mai jos);
b) decodorul raspunde la toate codurile pe 4 biti afisand caracterele din randul doi al reprezentarii de mai jos.
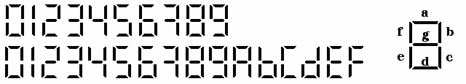
|