Interactiunea rotilor cu calea de rulare nedeformabila

Interactiunea rotilor cu calea de rulare nedeformabila

5.1. Cinematica rotilor autovehiculelor

Pentru simplificare, in studiul cinematicii rotilor de autovehicul, in scopul explicarii calitative a fenomenelor, seconsidera atat roata cat si suprafata pe care se rostogoleste aceasta sunt absolut rigide. i 121f51b n aceasta situatie, contactul dintre roata si drum se face dupa o dreapta a carei proiectie, in figura 37 este data de punctul O1, care reprezinta si axa instantanee de rotatie, I, in cazul rularii fara alunecare sau patinare. in realitate, deformatia rotii si solului este inevitabila si contactul intre roata si drum se face pe o suprafata, numita suprafata de sprijin a rotii. Functie de conditiile concrete de rostogolire a rotii, axa instantanee de rotatie poate ocupa diferite pozitii.

In cazul in care axa instantanee de rotatie I se afla pe suprafata de contact a rotii cu solul si coincide cu punctul O1 (fig.37,a), atunci dreapta de sprijin pe sol ramane imobila si ca urmare se produce rostogolirea ideala, fara alunecarea sau patinarea rotii.

Daca axa instantanee de rotatie I este plasata deasupra punctului de tangenta O1, zona de sprijin se deplaseaza in sens invers deplasarii autovehiculului, cu viteza v_d (fig. 37,b). in acest caz roata se rostogoleste cu patinare, iar viteza reala v_a de deplasare a autovehiculului este mai mica decat viteza teoretica v_t.

Daca axa instantanee de rotatie I este plasata sub zona de contact a rotii cu calea de rulare (fig. 37,c), iar zona de sprijin se deplaseaza in sensul deplasarii autovehiculului cu viteza v_d, roata se rostogoleste cu alunecare, iar viteza reala v_a de deplasare a autovehiculului este mai mare decat cea teoretica v_t.

Daca roata din figura 37,c este franata brusc, pana la blocare, centrul instantaneu de rotatie, I, se deplaseaza la infinit (fig. 37,d), iar miscarea devine o miscare de translatie in sensul deplasarii autovehiculului cu viteza v_d=v_a.

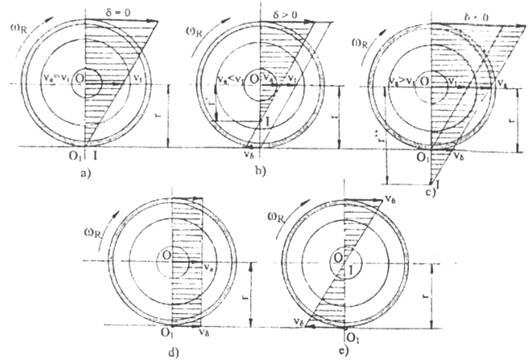
Fig. 37. Cinematica rotii de autovehicul.

In cazul in care aderenta rotii cu solul este foarte mica (cale de rulare acoperita cu gheata sau zapada), roata poate patina cu viteza v_d, fara ca autovehiculul sa se deplaseze v_a=0, iar miscarea devine o miscare de rotatie cu axa fixa (fig.37,e).

In figura 37, cu d s-a notat coeficientul patinarii sau al alunecarii,

In figura 38 este prezentata schematic o roata de raza r, care se rostogoleste fara patinare sau alunecare cu viteza unghiulara w_r pe un drum nedeformabil. Pe circumferinta rotii se considera un punct M, care se rostogoleste cu un unghi y La un anumit moment, punctul considerat are o viteza de rotatie v=r*w_r in jurul centrului rotii si o viteza de translatie de aceiasi valoare v. Prin compunerea celor doua viteze se cbtine o viteza rezultanta v_m ale carei componente v_x si v_z se pot determina grafic sau analitic. Marimea vitezei v_m si a componentelor sale v_x si v_z depinde de pozitia punctului considerat.

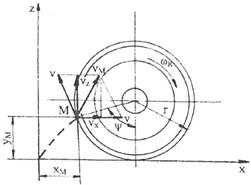
Fig. 38. Vitezele si deplasarile unui punct oarecare al rotii la rostogolirea acestuia.

d) fiind de sens contrar directiei de inaintare a autovehiculului, va avea loc o patinare a rotii, viteza de inaintare a autovehiculului fiind data de relatia:

v_a r'*w_R <r*w_R

Fenomenul de rostogolire cu patinare se intalneste la rotile motoare ale autovehiculelor, fiind caracterizat de coeficientul patinarii care se calculeaza cu relatia:

unde: I este drumul parcurs; n numarul de rotatii efectuat de roata pe distanta I; r raza dinamica a rotii.

5.2. Dinamica rotilor de autovehicul

In timpul deplasarii autovehiculului, rotile acestuia ruleaza pe suprafata drumului datorita uneia dintre urmatoarele actiuni:

• forta de impingere sau tragere F aplicata in centrul rotii, cazul rotii conduse fig40a

• un moment activ M_R, cazul rotii motoare figura 40,b;
• un moment de franare M_f, cazul rotii franate figura ,c.

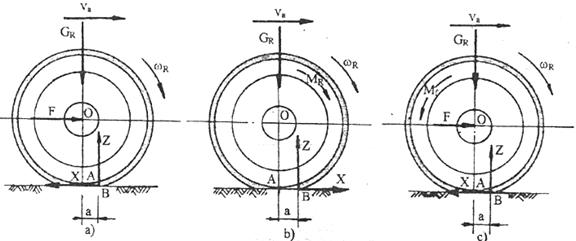
Fig. 40. Fortele si momentele care actioneaza asupra rotilor de autovehicul.

In functie de fortele si momentele care actioneaza asupra rotilor de autovehicule acestea pot fi: roti motoare sau antrenate, cand asupra lor actioneaza un moment motor M_R, care are acelasi sens cu viteza unghiulara w_R roti conduse sau neantrenate, cand asupra lor se aplica forte de impingere sau de tragere F, care au acelasi sens cu sensul de deplasare sau forte de retinere de sens opus sensului deplasarii; roti franate, cand asupra lor se aplica un moment de franare Mf, care are sens opus celui al vitezei unghiulare w_R

Ca urmare a actiunilor prezentate anterior, in zona de contact a rotii deformabile cu drumul nedeformabil ia nastere reactiunea tangentiale X si reactiunea normala Z, care sunt aplicate in punctul B, situat la distanta a fata de axa de simetrie a rotii OA.

Deplasarea punctului de aplicare a reactiunilor se datoreaza faptului ca deformatia pneului este mai mare in partea din fata a suprafetei de contact decat in partea din spate. in cazul rotii franate si a rotii conduse, figura 40,a si c, reactiunea tangentiala X este indreptata in sens invers deplasarii, iar in cazul rotii motoare aceasta este indreptata in acelasi sens cu deplasarea autovehiculului, constituind o forta de impingere care se numeste forta de tractiune la roata.

5.2.1. Echilibrul rotii motoare

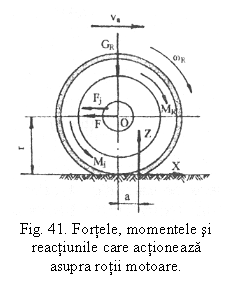
Daca se neglijeaza rezistenta aerului, fortele, reactiunile si momentele care actioneaza la rularea unei roti motoare sunt aratate in figura 41.

Daca rostogolirea rotii are loc cu viteza constanta, ea se deplaseaza sub actiunea momentului la roata Mr, care da nastere la o reactiune tangentiala X, in zona de contact dintre roata si drum, indreptata in acelasi sens cu deplasarea autovehiculului. Aceasta reactiune tangentiala se opune patinarii rotii si constituie o forta de impingere sau forta de tractiune la roata, care la randul ei da nastere la o reactiune F, egala si de sens contrar cu X, aplicata la axul rotii.

Reactiunea normala Z este egala cu greutatea repartizata pe roata Gr si in raport cu centrul rotii da nastere la moment de rezistenta la rulare M_r:

M,=Z-a.

Momentul la roata poate avea valori cuprinse intre o limita minima, sub care nu este posibila rularea rotii, si o limita maxima p este care incepe patinarea rotii. Limita minima este conditionata de egalitatea momentului Mr cu cea a momentului de rezistenta la rulare M_r. in acelasi timp limita maxima este conditionata de valoarea maxima a aderentei dintre roata si drum jZ. De aici, rezulta limitele posibile pentru reactiunea tangentiala la roata motoare, pentru ca aceasta sa ruleze fara patinare si anume:

F*Z<X j*Z. (40)

Din conditiile de echilibru a rotii motoare pentru miscarea uniforma (v_a=constant), scriind ecuatiile de proiectii pe axele orizontala si verticala si ecuatia momentelor in raport cu centrul rotii, se obtine:

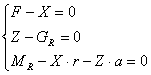
Cunoscand ca M_R=F_R.r, se poate scrie:

F_R=X+Z*a/r=X+f*Z (42)

sau daca avem in vedere ca reactiunea tangentiala X, reprezinta forta de tractiune F_t

F_R=F_I+F_r,   

de unde:

F,=F_R-F_r.   

Se poate trage concluzia ca forta de tractiune F_t este egala cu diferenta dintre forta periferica la roata datorata momentului M_R si forta de rezistenta la rulare F_f.

Daca se introduce limita maxima a reactiunii tangentiale data de relatia 40 in ecuatia de echilibru 42, se obtine conditia rularii fara patinare pentru miscarea uniforma:

F_R<Z*(f+ j

Valoarea maxima a fortei la roata F_R este limitata de conditia de aderenta, relatia pentru valori mai mari roata motoare patineaza.

In cazul deplasani accelerate ecuatiile de echilibru ale rotii motoare sunt:

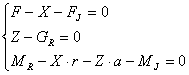
Sau

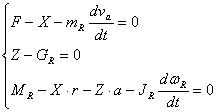
unde: Fj este forta de inertie a rotii, care se opune mariri vitezei de translatie; Mj, este

momentul fortei de inertie, care se opune accelerarii rostogolirii rotii; mr este masa rotii; Jr momentul de inertie al rotii in raport cu axa de rotatie; w_R este viteza unghiulara a rotii.

Cunoscand ca Mr=Fr*f, se obtine:

de unde:

sau:

Expresia fortei de tractiune F este:

Daca se introduce limita maxima a reactiunii tangentiale data de relatia 32 in ecuatia de echilibru 47, se obtine conditia rularii fara patinare pentru miscarea accelerata:

Analizand relatia 49 se poate trage concluzia ca la deplasarea rotii motoare in regim variabil, forta de tractiune este diminuata fata de regimul uniform de miscare cu valoarea fortelor de inertie care apar la accelerare.

5.2.2. Echilibrul rotii conduse

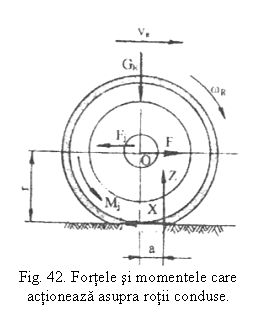Daca se neglijeaza rezistenta aerului, fortele, reactiunile si momentele care actioneaza la rularea unei roti conduse sunt aratate in figura 42. La rostogolirea rotii cu viteza constanta, deplasarea rotii are loc sub actiunea fortei F, aplicata la axul rotii, care determina aplicarea unei reactiuni tangentiale in zona de contact a rotii cu calea de rulare considerata nedeformabila. Aceasta reactiune, este indreptata impotriva sensului de deplasare a autovehiculului, si are valorile cuprinse intre:

f *Z<X≤jZ   

unde: f este coeficientul de rezistenta la rulare; j este coeficientul de aderenta.

Din conditia de echilibru a rotii conduse, in cazul deplasarii acesteia cu viteza constanta se obtin urmatoarele ecuatii de echilibru:

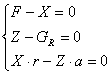
de unde:

X=Z*a/r=f*Z=F

Raportul a/r=f reprezinta coeficientul de rezistenta la rulare, care ia in considerare pierderile care au loc in timpul rularii rotii de autovehicul, iar forta de rezistenta la rulare pentru roata condusa este:

F_r=fZ

Daca in relatia se introduce limita maxima a reactiunii tangentiale din se obtine conditia rularii pentru roata condusa sub forma:

F*Z≤jZ sau f≤j

Daca coeficientul de aderenta are valori mai mici decat cele permise de conditia de rulare, 50, roata condusa nu mai ruleaza pe suprafata de rulare si incepe sa alunece in directia deplasarii autovehiculului.

In cazul deplasarii accelerate ecuatiile de echilibru ale rotii conduse sunt:

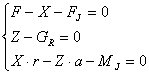
Sau

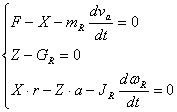
unde: Fj este forta de inertie a rotii, care se opune mariri vitezei de translatie; Mj este momentul fortei de inertie, care se opune accelerarii rostogolirii rotii; mr este masa rotii; Jr momentul de inertie al rotii in raport cu axa de rotatie; wr este viteza unghiulara a rotii. Din ecuatiile de echilibrul 54' rezulta:

sau:

Prin urmare, in cazul rularii rotii cu viteza variabila, forta de impingere sau tragere F trebuie sa invinga rezistentele la rulare a rotii si fortele de inertie ale acesteia, care apar in miscarea de rotatie si de translatie a rotii.