MODULATIA SEMNALELOR
q Introducere. Clasificari
Modulatia semnalelor a aparut din necesitatea transmiterii la distanta a informatiei, ca de exemplu sunete sau imagini.
Transmiterea simultana a mai multor semnale pe acelasi canal fizic de telecomunicatii este posibila prin utilizarea tehnicilor de multiplexare in frecventa sau in timp a semnalelor.
In procesul de modulatie intervin urmatoarele semnale:
Modulatia consta in modificarea unui parametru al purtatorului p(t) de catre semnalul modulator xm(t) ce urmeaza a fi transmis.
Dupa natura semnalului purtator, p(t), putem avea:
La receptie mesajul este extras din semnalul modulat printr-un proces denumit demodulare.
In cazul modulatiei cu purtator sinusoidal semnalul purtator are expresia:
unde A0 - amplitudinea purtatorului nemodulat
0 - frecventa unghiulara a semnalului purtator
0 - faza initiala a semnalului purtator
Fiecare din acesti trei parametri se poate modifica in functie de semnalul de modulatie, obtinandu-se urmatoarele tipuri de modulatie:
- modulatia de amplitudine (MA);
- modulatia de frecventa (MF);
- modulatia de faza (MP).
MODULATIA DE AMPLITUDINE CU PURTATOR SINUSOIDAL SI
AMBELE BENZI LATERALE (P+2BL)
a) semnalul modulator sinusoidal
b) semnalul purtator p(t)
c) semnalul MA, xMA(t)
Se observa ca spectrul semnalului MA contine trei componente armonice si anume:
- o componenta centrala de frecventa si amplitudine , care este chiar purtatorul;
- doua componente de frecvente si care au aceeasi amplitudine care se numesc componenta laterala inferioara, respectiv componenta laterala superioara.
Deoarece m≤1, rezulta ca amplitudinile componentelor laterale nu depasesc valoarea 0,5A0.
Banda de frecvente ocupata de semnalul MA este BMA=2fm
Presupunem ca semnalul MA obtinut folosind drept semnal modulator un semnal sinusoidal este, de exemplu, o tensiune aplicata la bornele unei rezistente R. Puterea disipata de acest semnal pe R va fi data de suma puterilor disipate de fiecare componenta spectrala pe rezistenta R, adica rezulta:
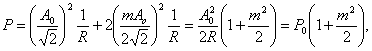
unde este puterea disipata de purtator pe
rezistenta R. Aceeasi expresie ca rel. (16) se obtine
pentru putere, in cazul cand semnalul MA este un curent, numai ca , I0 fiind amplitudinea
curentului purtator. Valoarea efectiva a semnalului MA rezulta din rel.:
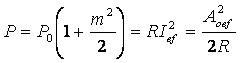
Se obtin relatiile valorilor efective pentru exprimari ale semnalului MA, tensiuni sau curenti:
Se observa ca modulatia de amplitudine, puterea si valoarea efectiva a semnalului MA cresc, in comparatie cu situatia cand nu avem modulatie. Cresterea este cu atat mai importanta cu cat gradul de modulatie este mai mare.
Cazul semnalului modulator sinusoidal ca suma de oscilatii sinusoidale
In aceasta situatie semnalul modulator are expresia:
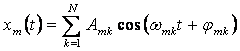
Functia de modulatie va fi:
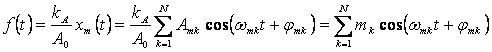
unde mk = kAAmk/A0. Rezulta expresia semnalului modulat:
purtatorul (k=0) avand frecventa F0 si amplitudinea
o infinitate de componente in banda laterala inferioara, avand frecventele F0 - kfm si amplitudinile
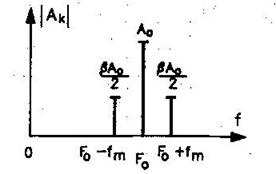
Un astfel de spectru este prezentat in fig. 1.20.
Fig. 1.20 Spectrul de amplitudini pt. un semnal MF
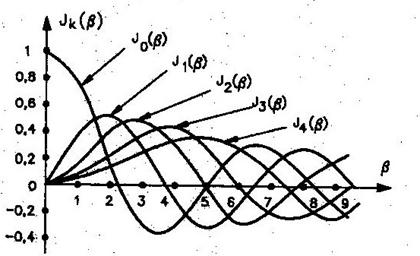
In fig. 1.21 sunt date reprezentarile grafice ale catorva functii Bessel de prima speta, de ordinul k si argument
In cazul in care este foarte mic, adica <0,4 expresia (86) poate fi prelucreta in felul urmator:
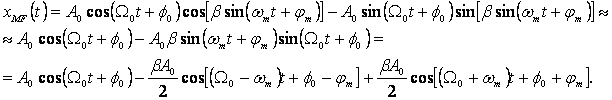
In acest caz spectrul de amplitudini contine numai trei componente si este reprezentat grafic in fig.1.22
Fig.1.22 Spectrul de amplitudini pt. un semnal MF cu xm(t) sinusoidal si <
In cazul <0,4 banda de frecventa ocupata de semnal este:
Expresia (87) pune in evidenta componentele spectrale ale semnalului MF, pentru un mare ( >0,4) . Se constata ca semnalul MF are un numar infinit de componente. Se poate insa arata ca practic largimea de banda de frecventa este limitata, deoarece pentru un dat, functiile Jk( ) au valori foarte mici pentru k mare, aproape toata energia semnalului MF este continuta in componentele spectrale localizate in interiorul unei benzi finite, asa cum se vede si din graficele din fig. 1.21.
<<1, cand formula (92) se reduce la expresia:
Rezultatul dat de relatia (94) este in concordanta cu cele aratate referitor la semnalul MF cu <0,4, cu semnal modulator sinusoidal.
Daca vrem sa calculam puterea disipata de un semnal MF cu semnal modulator
sinusoidal, folosim expresia (87) si pentru R=1 rezulta:
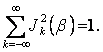
unde s-a tinut seama de relatia:
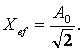Din relatia (95) rezulta de asemenea valoarea efectiva a semnalului MF:
Se observa deci prin modularea in frecventa sau in faza, puterea medie a semnalului nu se modifica, dar ea se repartizeaza tot mai mult pe componentele laterale pe masura ce creste. Dupa cum se poate vedea din fig. 1.21, exista valori ale lui pentru care J0( )=0 , deci purtatorul se anuleaza si toata puterea semnalului este repartizata in benzile laterale.
Pentru determnarea unei expresii a benzii de frecventa a semnalului MF uneori se face un rationament pe considerente energetice. Se impune conditia ca 99% din puterea semnalului MF sa se gaseasca in banda de trecere. Considerind puterile debitate pe o rezistenta de 1 , rezulta:
Ca urmare, N se poate determina din relatia:
Solutia aproximativa a ecuatiei transcendente (98) este:
ceea ce conduce la o banda efectiva:
Se observa ca pentru <<1 si pentru >>1 se obtin aceleasirezultate ca acelea analizate la utilizarea relatiei(92) pentru BMF. Expresia semnalului MP se obtine usor din cea a semnalului MF, inlocuind cu Ф si m cu m+ /2. Deci, in cazul semnalului modulator sinusoidal rezulta:
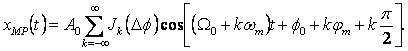
De asemenea, banda de frecventa a semnalului MP poate fi calculata, de exemplu, cu relatia:
in cazul semnalului modulator oarecare.
In situatia in care M<< 1, rezulta
BMP~2 ФMfmM=2kpmax|xm(t)|fmM
La semnalul MP componenta de frecventa superioara a semnalului modulator va necesita pentru transmisie o banda de frecventa a canalului nu va fi utilizata eficient de catre componentele de frecvente joase ale semnalului modulator in cazul MP. Din acest punct de vedere, sistemul MP este inferior sistemului MF.
|
