Masina asincrona – convertor electromecanic cu energie magnetica intermediara

Masina asincrona – convertor electromecanic cu energie magnetica intermediara

Masina asincrona foloseste energia magnetica ca energie intermediara in procesul transformarii energiei electrice in lucru mecanic. Astfel energia electrica se transforma in energie mecanica, iar variatia energiei magnetice datorita deplasarii armaturilor determina lucrul mecanic debitat.

Masina asincrona poate functiona si in regim de generator sau de frana.

In regim de generator masina transforma lucrul mecanic primit in energie electrica, iar in regim de frana masina transforma energia electrica si lucrul mecanic primit in caldura.

In cazul masinii asincrone sursele campului magnetic sunt bobine parcurse de curenti electrici variabili alternativi in timp.

1.1.      Principiul obtinerii cuplului electromagnetic

Functionarea convertoarelor electromagnetice se bazeaza pe doua fenomene cunoscute [1]:

a)           tendinta de aliniere a doua campuri magnetice, bazata pe atractia polilor de nume contrare;

b)          tendinta de aliniere a unei piese feromagnetice intr-un camp magnetic, bazata pe atractia piesei fata de polul cel mai apropiat.

In figura 1.1 cele doua campuri magnetice sunt produse de electromagneti determinati de infasurari asezate pe cele doua armaturi considerate circulare. Pentru simplificare armatura exterioara se considera fixa (stator), iar armatura interioara mobila (rotor).

In cazul in care polii celor doi electromagneti sunt aliniati, fig. 1.1 a, fortele de atractie dintre cei doi electromagneti nu determina cuplu; pozitia de functionare este stabila din punct de vedere mecanic.

Daca intre axele spatiale ale campurilor magnetice ale celor doi electromagneti exista un unghi de decalaj , fig. 1.1 b, atunci apare un cuplu de aliniere , numit cuplu electromagnetic, care are tendinta de a aduce cei doi electromagneti in pozitia stabila mecanic . Cuplul de aliniere are valoarea maxima corespunzator cazului in care unghiul de decalaj este .

Pentru un decalaj , cuplul electromagnetic este tot nul, fortele de respingere dintre cei doi electromagneti nu determina aparitia unui cuplu, fig. 1.1 c, aceasta pozitie fiind instabila. In figura 1.1 d este reprezentata valoarea cuplului de aliniere in raport cu unghiul de pozitie .

Fig.1.1.   Explicativa privind producerea cuplului electromagnetic in cazul in care cele doua armaturi sunt electromagneti

a)       cuplu nul;         b) cuplu de aliniere; c) cuplu maxim;

d)    variatia cuplului in raport cu pozitia armaturii interioare.

In figura 1.2 este prezentat cazul in care un rotor feromagnetic, fara surse de camp, este asezat in campul magnetic determinat de o infasurare dispusa pe stator. Magnetizarea rotorului se face prin influenta, astfel incat cuplul electromagnetic este nul indiferent de pozitia a rotorului.

Fig 1.3.      Explicativa privind producerea cuplului in cazul in care rotorul nu este perfect circular si nu este electromagnet:

a)       cuplu nul (θ=0);      b) cuplu de aliniere; c) cuplu nul (θ=π/2);

d)    variatia cuplului in raport cu pozitia rotorului.

Pentru a obtine cuplu electromagnetic este necesar ca rotorul sa nu mai fie de forma circulara, fig. 1.3. Daca rotorul este aliniat in campul magnetic al statorului, cuplul electromagnetic va fi nul, fig. 1.3 a si fig. 1.3 c. Conditia de a obtine cuplu electromagnetic nenul este ca rotorul sa aiba o deviatie diferita de valorile din punctele de echilibru, fig. 1.3 b. Pentru acest caz, in figura 1.3 d este reprezentata variatia cuplului electromagnetic in raport cu pozitia rotorului.

Cazul existentei unei singure perechi de poli, caz analizat mai sus, reprezinta o situatie particulara in constructia masinilor electrice; uzual se folosesc perechi de poli, unde .

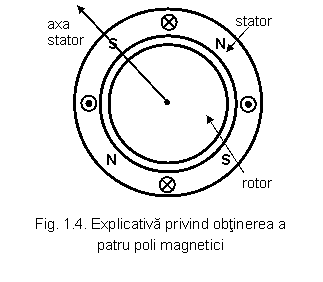In figura 1.4 s-a prezentat cazul in care la periferia unei armaturi sunt determinate doua perechi de poli magnetici . Se demonstreaza [2], [3] ca nu se poate obtine cuplu electromagnetic decat in cazul in care cele doua armaturi au acelasi numar de perechi de poli magnetici; in cazul in care una dintre armaturi nu este electromagnet, aceasta conditie este totdeauna respectata, fig. 1.3.

Asezarea simetrica a bobinelor determina o distributie simetrica a polilor magnetici la periferia armaturii.

1.2. Conditiile necesare obtinerii cuplului electromagnetic mediu nenul

Deoarece polii magnetici rotorici se deplaseaza odata cu rotorul, rezulta ca si polii magnetici ai statorului trebuie sa se deplaseze. Astfel, pentru obtinerea conditiei const., intre vitezele unghiulare trebuie sa existe relatia:

care asigura, prin sincronizarea campurilor magnetice, posibilitatea mentinerii constante a decalajului spatial ,fig. 1.5.

In egalitatea (1.1):

este viteza unghiulara de deplasare a armaturii interioare (rotorul), fig. 1.5; aceasta viteza este totdeauna pozitiva, rotorul deplasandu-se in sens pozitiv de referinta;

este viteza de deplasare a polilor statorici in raport cu propria armatura;

este viteza de deplasare a polilor rotorici in raport cu propria armatura;

este viteza unghiulara de deplasare a armaturii exterioare (statorul).

Fig. 1.5. Eplicativa privind sincronizarea vitezelor unghiulare ale campurilor magnetice

Daca consideram ca statorul este fix , in functie de posibilitatile de obtinere a campurilor magnetice invartitoare, convertoarele electromagnetice se pot clasifica astfel:

a)   Convertoare de tip asincron, in intrefierul carora se creeaza, pe ambele armaturi, cate un camp magnetic invartitor; cele doua campuri magnetice au vitezele unghiulare (campul statoric) si (campul rotoric) fata de propriile armaturi; viteza de rotatie a campului magnetic rotoric este corelata cu viteza unghiulara de deplasare a rotorului, astfel incat este satisfacuta conditia (1.1):

b)  Convertoare de tip sincron, in intrefierul carora numai una din armaturi determina un camp magnetic invartitor, cealalta armatura nedeterminand un camp magnetic propriu, sau determinand un camp magnetic fix.

Daca campul magnetic invartitor este determinat pe armatura stator si are viteza unghiulara , atunci pe rotor nu exista un camp magnetic invartitor , iar viteza unghiulara a rotorului trebuie sa satisfaca conditia (1.1):

Daca campul magnetic invartitor este determinat pe armatura rotor si are viteza unghiulara , atunci pe stator nu exista un camp magnetic invartitor , iar viteza unghiulara a rotorului trebuie sa satisfaca conditia (1.1):

Observatie:

Daca, de exemplu, viteza unghiulara a campului magnetic invartitor este constanta (const.) atunci, in cazul convertoarelor de tip asincron, conform egalitatii (1.2), viteza unghiulara a rotorului poate fi variabila datorita vitezei a campului magnetic invartitor rotoric. Cu aceeasi conditie (const.) din egalitatea (1.3 a) rezulta ca viteza unghiulara a rotorului este constanta in cazul convertoarelor de tip sincron. Situatia nu se schimba in cazul in care este constanta viteza unghiulara a campului magnetic rotoric (const.), vezi relatiile (1.2) si (1.3 a). Aceste doua proprietati explica denumirile celor doua tipuri de convertoare.

1.3. Modelul energetic in cazul functionarii in regim de motor

Consideram un convertor, functionand in regim termic stabilizat, care are circuite electrice si un circuit mecanic. In acest regim de functionare energia consumata de catre convertor este, integral, energie electrica, iar energia utila este lucru mecanic; ecuatia de bilant energetic este [2]:

,

unde:

este energia electrica primita pe la borne;

este energia corespunzatoare pierderilor Joule in conductoarele infasurarilor;

- energia magnetica;

este energia mecanica (cinetica si potentiala)

este lucrul mecanic consumat pentru a acoperi pierderile mecanice;

este lucrul mecanic util.

Bilantul energetic exprimat prin variatia energiei are forma:

unde:

si sunt tensiunea si curentul la bornele circuitului ;

este rezistenta circuitului electric ;

este variatia energiei consumata pentru acoperirea pierderilor in fier;

este variatia energiei magnetice stocate;

este variatia energiei mecanice;

este variatia lucrului mecanic consumat pentru acoperirea pierderilor mecanice;

este variatia lucrului mecanic util.

In egalitatea (1.4) se remarca separarea variatiei energiei magnetice in cele doua componente: variatia energiei necesare acoperirii pierderilor in fier si variatia energiei magnetice stocate .

In regim permanent viteza unghiulara este constanta si egala cu viteza si se poate considera ca:

variatia energiei mecanice stocata este nula: ;

variatia energiei se poate exprima in raport cu pierderile in fier care sunt constante: ;

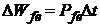variatia lucrului mecanic consumat se poate exprima in raport cu pierderile de frecari si ventilatie care sunt constante: ;

variatia lucrului mecanic util se poate exprima in raport cu valoarea cuplului mecanic care este constanta: ;

Astfel pentru regim permanent ecuatia de bilant (1.4) exprimata prin variatia energiei devine:

unde s-a efectuat notatia:

- puterea consumata pentru acoperirea pierderilor Joule.

Ecuatia (1.4) sugereaza un model energetic al convertorului, model prezentat in figura 1.6a.

Se observa ca, din punct de vedere functional, elementele constructive ale unui convertor se pot grupa in trei sisteme energetice: sistemul electric (format din infasurarile convertorului), sistemul de conversie (format din circuitul feromagnetic) si sistemul mecanic (format din elementele mecanice: lagare, ventilatoare). Fiecare sistem are pierderile lui specifice.

In figura 1.6 a este prezentat modelul energetic corespunzator functionarii in regim permanent – vezi ecuatia de bilant (1.4 a).

Energia corespunzatoare acestor pierderi este transmisa in exterior sub forma de caldura. In figura 1.6 a, pentru simplificare s-a desenat numai circuitul electric cu numarul .

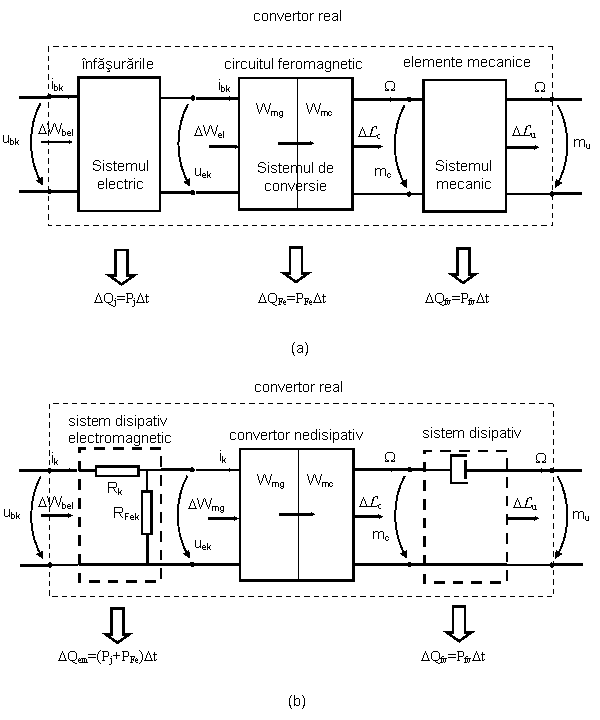
Fig. 1.6. Modelul energetic al unui convertor:

a)   modelul convertorului real;

b)   modelul pentru cazul regimul permanent de functionare.

Prin separarea sistemelor disipative electromagnetice si mecanice, se defineste o noua structura: convertorul nedisipativ. Acesta este format din circuitul magnetic si infasurarile convertorului real, dar nu are pierderi.

Bilantul energetic al convertorului nedisipativ functionand in regim permanent rezulta din ecuatia generala de bilant (1.4 a), fig.1.6 b.

unde:

este variatia energiei magnetice primita, egala cu variatia energiilor electrice transferate de catre infasurari

este tensiunea electromotoare rezultanta indusa in infasurarea ;

este curentul care parcurge infasurarea, dupa separarea pierderilor in fier;

este puterea electrica primita de convertorul nedisipativ

;

este variatia lucrului mecanic total debitat de convertor.

Variatia energiei magnetice primita poate fi exprimata si prin variatia fluxurilor magnetice din infasurari, daca consideram legea inductiei electromagnetice.

Daca consideram expresia lucrului mecanic total in raport cu valoarea cuplului mecanic total, , in ipoteza fluxurilor magnetice constante (), din ecuatiile (1.5 a) si (1.5 a), se obtine expresia cuplului mecanic total:

unde cu s-a notat variatia pozitiei unghiulare a armaturii mobile. Trecand la limita in ecuatia (1.6), rezulta:

Relatia (1.6) arata ca valoarea cuplului mecanic este egala cu valoarea cuplului electromagnetic calculat prin folosirea teoremei fortelor generalizate. Conform acestei teoreme, pentru medii liniare se poate utiliza una din expresiile:

Observatie

In cazul in care energia magnetica se considera inmagazinata in campul magnetic al circuitelor electrice (infasurari) expresia cuplului electromagnetic instantaneu (1.7), in ipoteza considerarii curentilor constanti devine [5]:

unde:

este matricea coloana a curentilor care parcurg infasurarile;

este matricea patrata a inductivitatilor mutuale;

este matricea transpusa a curentilor.

Pentru functionarea in regim permanent ca motor, considerand ecuatia de bilant (1.4 a), se poate defini randamentul convertorului , exprimat astfel:

unde:

         reprezinta puterea electrica activa primita de convertor;

este suma pierderilor de putere in convertor: pierderile in fier , pierderile Joule si pierderile mecanice .

Observatie

In cazul functionarii in regim de generator expresia randamentului este:

1.4 Modelul energetic al masinii asincrone

Dupa cum rezulta din clasificarea convertoarelor electromecanice, masina asincrona este un convertor caracterizat de existenta a doua campuri magnetice invartitoare, determinate, cate unul, pe fiecare armatura. In constructie clasica infasurarea statorica este cuplata de la retea, iar infasurarea rotor este in scurtcircuit.

In figura 1.7 este prezentat modelul energetic al masinii asincrone, functionand ca motor. Modelul separa elementele disipative, si este rezultat din modelul general prezentat in figura 1.6 b. S-au prezentat separat, printr-un singur circuit infasurarea statorica, respectiv infasurarea rotorica.

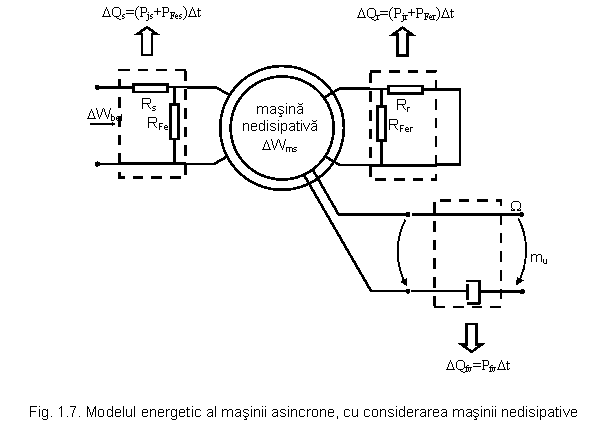
Considerand ecuatia de bilant (1.4 a) pentru cazul functionarii masinii in regim permanent:

,

se obtine bilantul puterilor active:

unde:

reprezinta puterea activa primita pe la bornele infasurarile stator;

si - pierderile Joule in infasurarile stator, respectiv rotor;

si - pierderile in circuitul feromagnetic al statorului, respectiv al rotorului;

- pierderile de frecari si ventilatie;

- puterea mecanica.

Egalitatea (1.9) poate fi scrisa si sub forma:

unde:

reprezinta puterea activa consumata pe stator

reprezinta puterea activa consumata pe rotor

reprezinta puterea mecanica la ax

Din ecuatia de bilant (1.10) se poate separa componenta puterilor active consumata pe rotor :

precum si bilantul puterilor active pentru stator:

,

unde este puterea electromagnetica transferata prin intermediul campului electromagnetic de la stator la rotor.

Comparand egalitatile (1.9), (1.11) si (1.12) se observa egalitatea puterii electromagnetice cu puterea consumata pe rotor: