Masina asincrona

Masina asincrona

a

Masina asincrona este utilizata pe scara larga in actionarile electrice, cu precadere in regim de motor trifazat, in majoritatea sectoarelor industriale: actionarea masinilor unelte, a pompelor, a compresoarelor, a poduril 454c22e or rulante, a elevatoarelor, etc. De remarcat, in ultimul timp, patrunderea agresiva a masinii asincrone in domeniul tractiunii electrice, mai cu seama de cand, alimentarea acesteia prin invertoare cu modulare in latime a impulsurilor nu mai constituie un impediment, din punct de vedere al eficientei economice. Trebuie amintita aici si utilizarea masinii asincrone ca generator, in centralele electrice de mica putere, de tip hidro sau eolian.

Motoarele asincrone se construiesc intr-o gama foarte larga de puteri (de la unitati de watt pana la ordinul zecilor de MW) si avand turatia sincrona, la frecventa de 50 Hz, egala in mod uzual cu 500, 600, 750, 1000, 1500 sau 3000 rot/min, in functie de numarul de perechi de poli. Motoarele asincrone prezinta o constructie relativ simpla si robusta in functionare.

1.1. Constructia masinii asincrone.

In constructie clasica, masina asincrona se compune dintr-un stator si un rotor concentric cu statorul, dispus in interiorul acestuia.

Statorul - constituie partea imobila a masinii, fiind format din miezul feromagnetic pe care se dispune o infasurare trifazata. Miezul este asezat intr-o carcasa cu rol de protectie si consolidare.

Miezul feromagnetic are forma cilindrica si se executa din tole stantate din tabla silicioasa normal aliata, de 0,5 mm grosime (de obicei), laminata la cald sau la rece; tolele sunt izolate intre ele cu o pelicula de lac izolant sau printr-un strat de oxizi ceramici. In tole, spre intrefier, se stanteaza crestaturile, repartizate uniform, in care se aseaza infasurarea. Infasurarea statorica este repartizata si prin intermediul ei masina efectueaza schimbul principal de energie electrica cu reteaua de alimentare. Infasurarea se executa din conductor de Cu izolat sau, la masinile de puteri mici, din conductor de Al, izolat cu email. La masina asincrona trifazata infasurarea statorului se conecteaza in stea sau triunghi. La masinile de puteri mici si mijlocii, infasurarea trifazata are toate capetele infasurarilor de faza scoase la cutia de borne, pentru a face posibila conectarea acestora in stea sau triunghi, dupa necesitati. Fiecare infasurare de faza este bobinata pentru acelasi numar de poli.

Carcasa - se executa prin turnare, din aluminiu sau fonta, sau prin sudare, din tabla de otel. Carcasa poarta talpile de fixare a masinii, inelul de ridicare, cutia de borne, placuta indicatoare si scuturile frontale. In scuturi se monteaza lagarele pe care se sprijina axul rotorului.

Rotorul - constituie partea mobila a masinii asincrone si se compune din miezul feromagnetic, de forma cilindrica, la periferia caruia (spre intre-fier), sunt prevazute crestaturile in care se aseaza o infasurare polifazata. Miezul feromagnetic al rotorului se realizeaza din tole, din acelasi material ca si statorul, dar tolele nu se izoleaza intre ele. Pachetul de tole rotorice se consolideaza pe axul masinii.

Axul se roteste in lagarele montate in scuturi, fiind elementul de transmisie a energiei mecanice intre masina electrica si exterior. Tot pe ax, in majoritatea cazurilor, este fixat si un ventilator, cu rol de racire a masinii. La masinile care permit o legatura galvanica intre infasurarea indusului (rotorul) si un circuit electric exterior, pe ax se monteaza si inelele de contact, pe care calca periile (fixe fata de stator).

Infasurarea rotorului, la masina asincrona de constructie normala, se realizeaza cu acelasi numar de poli ca infasurarea statorica si se construieste fie ca infasurare trifazata (bobinata), fie ca infasurare polifazata (sub forma de colivie). Infasurarea bobinata se executa din conductor de Cu sau Al izolat, iar infasurarea in colivie (sau in scurtcircuit) din bare de Cu, Al sau alama; colivia din Al se executa prin turnare. Infasurarea in colivie nu este izolata fata de miezul feromagnetic al rotorului. Infasurarile bobinate se executa ca infasurari trifazate si se conecteaza in stea sau triunghi, iar capetele libere ale celor trei infasurari de faza se conecteaza la inelele de contact.

Infasurarile in colivie sunt infasurari polifazate, barele coliviei fiind scurtcircuitate frontal prin inele conductoare.

Intrefierul - este spatiul liber ramas intre miezul feromagnetic al rotorului si miezul statorului. Largimea intrefierului la masina asincrona este practic constanta (daca neglijam deschiderea crestaturilor) si are o valoare foarte mica (0,1 2 mm), in vederea obtinerii unui curent de magnetizare cat mai mic, respectiv a unui factor de putere ridicat.

1.2. Principiul de functionare.

Se considera o masina electrica rotativa formata din doua armaturi cilindrice, concentrice, de constructie normala, a carei infasurare statorica este conectata la o retea trifazata simetrica de alimentare, de frecventa f₁. Circuitul rotoric se considera scurtcircuitat sau inchis pe un reostat simetric.

Infasurarea statorica, inductorul, parcursa de un sistem trifazat simetric de curenti avand frecventa f₁, genereaza in circuitul magnetic al masinii un camp magnetic invartitor. Viteza unghiulara a campului invartitor W , numita viteza de sincronism, este determinata de pulsatia ω₁ = 2·π·f₁, a curentilor si de numarul de perechi de poli, p, realizati de infasurare, pe o faza:

Ω₁ = ω₁/p [rad/s]. (1.1)

Din aceasta relatie se obtine turatia de sincronism, , a campului magnetic invartitor:

sau, . (1.2)

Campul magnetic invartitor intersecteaza bobinele rotorice in ordinea succesiunii lor, astfel incat, in aceste infasurari, se induc tensiuni electromo-toare formand un sistem trifazat simetric. Intrucat circuitele rotorice sunt inchise, de-a lungul lor se stabileste un sistem trifazat (rotor bobinat) sau polifazat (rotor in scurtcircuit) de curenti electrici.

Din interactiunea camp magnetic inductor - curenti rotorici, rezulta forte care actioneaza tangential la rotor, generand fata de arborele masinii un cuplu electromagnetic

Rotorul este pus in miscare cu o viteza unghiulara W, careia ii corespunde o turatie n, in sensul campului magnetic invartitor.

Fenomenul de inductie electromagnetica fiind conditionat de existenta unei miscari relative a campului invartitor fata de rotor, e necesar ca viteza unghiulara a rotorului sa difere de viteza de sincronism, deci, W W

Miscarea relativa a rotorului fata de campul invartitor este descrisa de marimea numita alunecare, s, definita astfel:

. (1.3)

Pe baza relatiei de definitie a alunecarii se pot evidentia regimurile de functionare ale masinii asincrone - figura 1.1.

Figura 1.1. Regimurile de functionare a masinii asincrone.

In regim de motor, pentru ca masina sa dezvolte cuplu electromagnetic, trebuie indeplinita conditia: 0 ≤ W < W ; alunecarea este cuprinsa in domeniul 0 £ s £ . Alunecarea s = 1, corespunde momentului pornirii, cand rotorul este imobil, iar valoarea s = 0, corespunde mersului in gol ideal al motorului.

Deoarece interactiunea dintre infasurarea rotorica si campul invartitor, inductor, este dependenta de alunecare, frecventa curentilor rotorici este diferita de frecventa curentilor statorici. Viteza unghiulara a campului magnetic invartitor fata de rotorul aflat in miscare fiind W W, pulsatia marimilor electrice rotorice este:

(1.4)

si utilizand relatiile (1.1) si (1.3), se obtine:

sau, . (1.5)

Infasurarea rotorica, parcursa de curenti electrici cu frecventa f₂, produce la randul ei un camp magnetic invartitor, camp magnetic de reactie, care se deplaseaza, fata de rotor, cu turatia:

. (1.6)

Turatia campului rotoric, fata de stator, se obtine insumand turatia acestuia fata de rotor, n₂, cu turatia rotorului, n:

. (1.7)

Se observa ca, turatia campului de reactie este egala cu cea a campului statoric.

Prin compunerea campului inductor cu campul de reactie, in intrefier se obtine un flux magnetic rezultant, generator de cuplu electromagnetic si care induce in infasurarile statorice tensiuni electromotoare avand frecventa egala cu cea a retelei de alimentare.

Din principiul de functionare se constata o asemanare fenomenologica intre masina asincrona si transformatorul electric trifazat, de aceea se poate spune ca, masina asincrona, numita si masina de inductie, se comporta ca un transformator dinamic.

1.3. Ecuatiile de functionare.

Se considera o masina trifazata simetrica, alimentata in stator de la o sursa trifazata simetrica, de frec-venta f₁. Se presupune ca masina functioneaza intr-un regim elec-tromagnetic stationar, nu are pierderi in miezul feromagnetic, circuitul magnetic este liniar, iar infasurarile sunt repartizate sinu-soidal, astfel incat curba campu-lui magnetic din intrefier este o unda sinusoidala. Circuitul roto-ric se considera scurtcircuitat sau inchis (figura 1.2).

Presupunem ca rotorul se in-varte cu o turatie constanta n < n₁ in sensul campului invartitor (masina in regim de motor).

Se fac urmatoarele notatii:

- tensiunea de faza statorica;

i₁ - curentul printr-o faza (oarecare) din stator;

i₂ - curentul pe faza in rotor;

R₁, R₂ - rezistentele pe faza ale celor doua circuite (stator, respectiv rotor); in valoarea rezistentei R₂ este inclusa si rezistenta pe faza a reostatului din circuitul rotorului.

L_s , L_s - inductivitatile de dispersie pe faza, statorica, respectiv rotorica.

Se presupune ca rotorul are turatia n, corespunzatoare unei alunecari s, iar inductivitatile L_s si L_s sunt constante.

Intrucat, , se pot pune in evidenta fluxurile prin infasurarile de faza statorice, respectiv rotorice:

; (1.8)

; (1.9)

reprezinta variatia fluxurilor de scapari statorice si rotorice.

La masina cu circuitul magnetic liniar, fluxurile totale ale campului magnetic rezultant, intr-o infasurare de faza, sunt (indicele "1" se refera la stator, "2" la rotor):

; (1.10)

F - fluxul produs de campul invartitor creat de infasurarea primara, care inlantuie spirele unei faze statorice, de pulsatie w

F - fluxul care inlantuie spirele unei faze statorice, dar produs de campul invartitor rotoric; fata de statorul imobil, acesta va avea tot pulsatia w , deoarece fundamentala campului invartitor produs de infasurarea rotorica are, fata de stator, turatia n₁ (am vazut aceasta anterior), iar intre pulsatie si turatie exista relatia:

; (1.11)

F - fluxul produs de campul invartitor creat de infasurarea rotorica parcursa de curentii respectivi, care inlantuie spirele unei faze rotorice - fundamentala sa va avea, fata de rotor, pulsatia w

F - fluxul care inlantuie spirele unei faze rotorice, dar produs de campul invartitor creat de curentii statorici; pulsatia fundamentalei acestuia, fata de rotor, va fi w , deoarece campul invartitor produs de stator are, fata de rotor (aflat in miscare cu turatia n), turatia:

. (1.12)

Observam ca, marimile electrice din ecuatia (1.8), corespunzatoare circuitului primar, au pulsatia w , iar cele din ecuatia (1.9), corespunzatoare secundarului, au pulsatia w . Aplicand transformarea in complex simpli-ficata obtinem:

(1.13)

(1.14)

Deoarece w ¹ w , planurile complexe in care sunt reprezentate cele doua ecuatii sunt diferite

Inlocuind in (1.14), ω₂ = sω₁, obtinem sistemul:

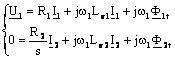(1.15)

Aceste ecuatii corespund unei masini asincrone echivalente, care ar avea rotorul fix fata de stator (in aceasta situatie n = 0; s = 1; w w ), iar in circuitul secundar ar fi conectata rezistenta R_s = R₂/s - R₂, deoarece, pe faza rezistentei R₂, in ecuatia (1.15), apare rezistenta R₂/s.

Exprimand fluxurile magnetice Φ_1t si Φ_2t in functie de fluxul fascicular util Φ_u si notand ω₁L_σ1 = X_σ1, ω₁L_σ2 = X_σ2, ecuatiile (1.15) devin:

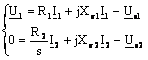(1.16)

Figura 1.3. Schema echivalenta a masinii asincrone ideale.

Recurgand la procedeul de raportare a infasurarii rotorice la stator si introducand rezistenta echivalenta pierderilor in miez, se obtine, pentru masina asincrona, sistemul de ecuatii (1.17) si schema echivalenta din figu-ra 1.4.

, (1.17)

in care:

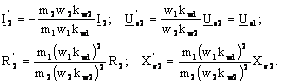(1.18)

Figura 1.4. Schema echivalenta "in T" a masinii asincrone.

Observatii:

Intrucat la masina asincrona infasurarile sunt repartizate in crestaturi, numarul de spire w₁ sau w₂ trebuie "corectat" intotdeauna prin k_w1, respectiv k_w2 (factorul de infasurare corespunzator).

Se tine cont si de faptul ca, la masina asincrona numarul de faze al infasurarii primare poate fi diferit de cel al infasurarii secundare (m₁ ¹ m₂). Pentru rotorul in scurtcircuit avem: m₂ = Z₂; w₂ = 1/2; k_w2 = 1 (Z_1,2 - numarul de crestaturi statorice, respectiv rotorice).

O varianta, oarecum simplificata, a schemei echivalente din figura 1.4 este cea reprezentata in figura 1.5. Cele doua scheme echivalente ale masi-nii asincrone cu pierderi in miez, sunt cunoscute sub numele de scheme "in T ".

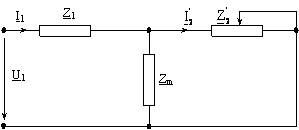
Figura 1.5. Varianta a schemei echivalente "in T" a masinii asincrone.

In schema din figura 1.5 s-au folosit urmatoarele notatii:

G " (figura 1.6), in care, s-au facut notatiile:

si ; (1.20.a,b)

se observa ca:

. (1.21)

Componenta reprezinta curentul prin circuitul primar al masinii asincrone la functionarea in gol ideal (corespunzator alunecarii s = 0).

In expresia componentei s-a notat cu:

; (1.22)

modulul acestui factor complex poate fi scris aproximativ astfel:

; (1.22.a)

c₁ reprezinta, in acest caz, coeficientul total de dispersie. La masinile normale valoarea acestui factor este: c₁ = 1,04 . 1,08.

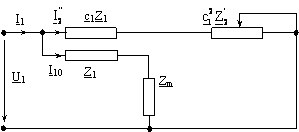
Figura 1.6. Schema echivalenta "in G" a masinii asincrone.

Se poate demonstra ca, intre curentii rotorici ai masinii, din cele doua scheme, exista relatia:

. (1.23)

Transfigurarea schemei electrice echivalente din "T ", in " G ", mentine neschimbate pierderile in circuitul secundar, adica:

, (1.24)

deoarece, dupa cum rezulta din relatia (1.23), intre modulele compo-nentelor si exista relatia:

.

Pentru simplificare, impedantele din latura derivatie a schemei elec-trice " in G " se noteaza, in mod uzual, cu litere mici:

Corespunzator cazului in care c₁ este aproximat prin modulul sau, rezulta:

(1.25.a)

1.4. Bilantul puterilor motorului asincron.

Deoarece, la masina asincrona normala, nu are loc schimb de putere reactiva pe la bornele circuitului rotoric, intereseaza, in special, circulatia puterilor active.

Inmultind ecuatiile tensiunilor masinii asincrone (1.17) cu (prima ecuatie), respectiv cu (cea de-a doua ecuatie), in urma efectuarii calculelor, rezulta:

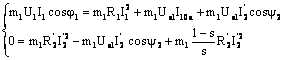; (1.26)

in care:

La motorul asincron s I , iar defazajul j I p . Din prima ecuatie (1.26) se pot trage urmatoarele concluzii: o parte din puterea absor-bita de motor,

P₁ = m₁U₁I₁cosj (1.27)

este transformata in pierderi Joule in circuitul primar,

(1.28)

si in pierderi in miezul feromagnetic,

P_Fe1 = m₁U_e1I_10a; (1.29)

in care, (I₁₀ cosa = I_10a); ;

cea mai mare parte insa,

, (1.30)

este transmisa pe cale electromagnetica rotorului. Se poate scrie:

. (1.31)

Din cea de-a doua ecuatie (1.26), se observa ca, o parte din puterea primita pe cale electromagnetica de secundar (rotor) se pierde in infasu-rarea rotorica prin efect Joule,

, (1.32)

iar diferenta:

(1.33)

este transformata in putere mecanica, transmisa "efectiv" rotorului si, prin acesta, axului masinii. Prin urmare:

; (1.34)

pierderile in miezul feromagnetic al secundarului se pot neglija deoarece frecventa marimilor electrice din infasurarea acestuia, f₂ = s f₁, este mica (f₂ < 5 Hz).

Din puterea mecanica, o parte se transforma in pierderi de frecare si ventilatie P_f,v, o parte acopera pierderile suplimentare care apar in miez in regimul de functionare, P_sFe, iar diferenta se transmite axului sub forma de putere utila, P_ax:

. (1.35)

In figura 1.7 s-a reprezentat grafic bilantul puterilor active pentru regimul de motor.

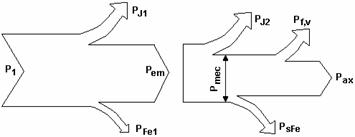
Figura 1.7. Repartitia puterilor active la motorul asincron.

1.5. Cuplurile masinii asincrone.

1.5.1. Cuplul electromagnetic.

In regim permanent, motorul asincron echilibreaza cuplul de sarcina, format din cuplul rezistent la mers in gol, M₀, si cuplul rezistent util, M_ax.

Cuplul electromagnetic, M, dezvoltat de rotorul motorului, daca acesta se roteste cu turatie constanta, este constituit din doua componente, fiecare din acestea fiind in echilibru cu componentele corespondente ale cuplului de sarcina:

M = M₀ + M_ax; (1.36)

in care:

; (1.37)

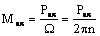; (1.38)

W - viteza unghiulara a rotorului;

n - turatia.

Cuplul electromagnetic, M, apare ca urmare a interactiunii dintre fluxul magnetic invartitor, rezultant, f_u, si curentul I₂, care parcurge infasurarea rotorului. Deoarece fluxul f_u se roteste in spatiu cu viteza unghiulara W pn₁, puterea dezvoltata de acesta este tocmai puterea electromagnetica a motorului, P_em:

. (1.39)

Tinand cont de expresia puterii electromagnetice (1.30) si de schemele echivalente ale masinii asincrone, cu pierderi in miez ("in T " si "in G "), expresia cuplului electromagnetic poate fi scrisa sub forma urmatoare:

. (1.40)

Relati (1.40) este valabila pentru toate valorile alunecarii, adica pentru toate regimurile de functionare a masinii.

1.5.2. Cuplul electromagnetic maxim.

Pe baza relatiei (1.40), prin derivare, se poate determina expresia cuplului electromagnetic maxim, M_max.

Derivata se anuleaza pentru:

. (1.41)

Semnul "+" corespunde functionarii masinii asincrone ca motor, iar semnul "-" functionarii masinii in regim de generator.

La masinile asincrone normale valoarea lui r₁ este mult inferioara valorii , deci poate fi neglijata in expresia alunecarii s_m:

. (1.41.a)

Introducand expresia (1.41), obtinuta pentru alunecare, in relatia (1.40), gasim expresia cuplului electromagnetic maxim:

; (1.42)

unde, semnul "+" corespunde, de asemenea, functionarii in regim de motor, iar semnul "-" regimului de generator.

Neglijand in expresia (1.42) valoarea lui , ajungem la expresia aproximativa a cuplului electromagnetic maxim:

. (1.42.a)

Observatii.

a)    Pentru o masina data, la frecventa constanta, cuplul electromag-netic maxim este proportional cu patratul tensiunii de alimentare.

b)   Cuplul electromagnetic maxim nu depinde de rezistenta circuitului rotoric.

c)    Cuplul maxim se obtine pentru o alunecare, s_m, care este cu atat mai mare, cu cat raportul este mai mare, sau, cu cat rezistenta circuitului rotoric este mai mare.

d)   Pentru o frecventa data, cuplul este aproximativ invers proportional cu suma reactantelor , cu alte cuvinte, cuplul este cu atat mai mic, cu cat reactantele de dispersie ale circuitelor masinii sunt mai mari.

Valoarea cuplului M_max are o importanta deosebita in cazul in care masina functioneaza ca motor, cuplul maxim al masinii asincrone fiind numit si cuplu reversibil sau critic. Raportul

(1.43)

se numeste coeficient de supraincarcare a motorului asincron.

1.5.3. Cuplul de pornire al motorului asincron.

Cuplul de pornire, M_p, ca si cuplul maxim, este una dintre carac-teristicile cele mai importante ale motorului. Valoarea cuplului de pornire se obtine din relatia (1.40), pentru s = 1:

. (1.44)

Daca dorim un cuplu de pornire cat mai mare, trebuie, dupa cum rezulta din expresia (1.41), sa avem:

a)    Pentru o frecventa data, f₁, si parametrii motorului dati, cuplul de pornire este proportional cu patratul tensiunii de alimentare.

b)   Cuplul de pornire atinge valoarea maxima daca rezistenta circu-itului rotoric este egala cu reactanta de dispersie a masinii.

1.6. Caracteristica mecanica a motorului asincron.

Pentru studiul calitativ al dependentei cuplului electromagnetic de alunecare, se utilizeaza o expresie a cuplului simplificata, valabila in cazul motoarelor asincrone de putere (formula Kloss):

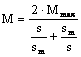, (1.47)

unde, M_max reprezinta valoarea maxima a cuplului, iar s_m alunecarea corespunzatoare acestui cuplu.

In figura 1.8.a, s-a reprezentat grafic variatia cuplului in functie de alunecare, in conformitate cu relatia (1.47).

Functionarea stabila a motorului este posibila numai pe ramura "0 - K" a caracteristicii, deci pentru alunecari cuprinse intre 0 si s_m si cupluri cuprinse intre 0 si M_max.

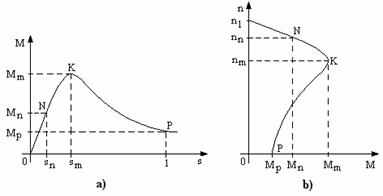
Figura 1.8. a) Caracteristica "cuplu - alunecare" a motorului asincron.

b) Caracteristica mecanica, n = f(M).

Pe caracteristica sunt evidentiate punctele definitorii pentru functiona-rea unui motor asincron:

punctul P, corespunzator pornirii, caracterizat prin alunecarea s = 1, deci n = 0 si cuplul de pornire M_p, a carui expresie se obtine din relatia (1.47), pentru s = 1:

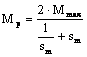; (1.48)

punctul critic de functionare, K, corespunzator alunecarii s_m (numita si alunecare critica) si cuplului maxim, M_max;

punctul nominal de functionare, N, caracterizat prin alunecarea nominala, s_n si cuplul nominal, M_n;

punctul corespunzator mersului in gol ideal, caracterizat prin s = 0, deci n = n₁ si M = 0.

Caracteristica mecanica reprezinta dependenta n = f(M).

Ecuatia ei se obtine din relatia (1.47), prin inlocuirea alunecarii cu turatia corespunzatoare, conform relatiei de definitie a acesteia. Forma caracteristicii mecanice este reprezentata in figura 1.8.b.

Dependenta n = f(M), obtinuta in cazul alimentarii motorului cu tensiune nominala, la frecventa nominala, circuitele rotorice exterioare avand rezistenta nula (in cazul masinii cu rotorul bobinat), se numeste caracteristica mecanica naturala.

Caracteristicile obtinute prin modificarea tensiunilor de faza, a frecven-tei sau rezistentei rotorice exterioare, se numesc caracteristici mecanice artificiale.