Modele matematice simplificate

Modele matematice simplificate

Se considera un transformator monofazat avand o caracteristica magnetica liniara, care satisface toate ipotezele si conditiile impuse in partea introductiva a paragrafului II 2.2.

In figura 2.5 este prezentata o reprezentare conventionala a transformatorului function 555g62f and in sarcina, pe care a fost pus in evidenta un spectru succint al liniilor de camp magnetic:

campul magnetic rezultant, care este camp magnetic util, se inchide pe circuitul feromangetic si inlantuie ambele infasurari;

campul magnetic de dispersie al infasurarii primare, care inlantuie numai spire ale infasurarii primare;

campul magnetic de diseprsie al infasurarii secundare, care inlantuie numai spire ale infasurarii secundare.

Campul magnetic de dispersie al infasurarii primare, in raport de infasurarea secundara se inchide prin aer si, eventual, partial prin circuitul feromagnetic. Reluctanta magnetica a zonelor de aer este constanta, iar reluctanta magnetica corespunzatoare zonelor circuitului magnetic este mult mai mica decat reluctanta zonelor de aer (permeabilitatea magnetica corespunzatoare portiunilor din circuitul feromagnetic este mult mai mare decat permeabilitatea magnetica , a portiunilor din aer, indiferent de nivelul de saturatie al circuitului magnetic). In consecinta, fluxul magnetic determinat in infasurarea primara de catre campul magnetic propriu de dispersie poate fi considerat liniar dependent de curentul infasurarii proprii:

(2.10 a)

unde constanta de proportionalitate este inductivitatea de dispersie a infasurarii primare in raport cu infasurarea secundara - vezi relatia

In mod similar se poate defini inductivitatea de dispersie a infasurarii secundare in raport cu infasurarea primara - vezi capitolul I 5.3 si egalitatea

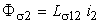(2.10 b)

Campul magnetic rezultant (util) este impus de solenatia rezultanta (vezi paragraful..

si determina prin infasurari fluxurile utile - vezi egalitatiile (2.4 a) si (2.4 b)

si (2.11)

Considerand relatiile (2.10 a), (2.10 b) si (2.11), fluxurile magnetie totale ale celor doua infasurari au expresiile:

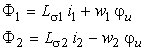(2.11 b)

Daca inlocuim aceste expresii in sistemul (2.3) se obtine modelul matematic al transformatorului monofazat, simplificat prin liniarizarea caracteristicii magnetice cu considerarea neliniaritatii circuitului magnetic:

(2.12)

unde u_e1 reprezinta tensiunea electromotoare indusa de fluxul total in infasurarea primara, iar cu s-a notat inductivitatea utila

Ecuatiile modelului matematic (2.12) sugereaza structura modelului de circuit prezentat in figura 2.6. Pe acest model s-au precizat zonele care corespund fiecarui element din structura unui convertor electric conform paragrafului I 4.3 si figurii 1.10 a.

Considerand neglijabile caderile de tensiune pe rezistentele si inductivitatile de dispersie ale infasurarilor din ecuatiile (1) si (4) ale modelului matematic (2.12):

respectiv

rezulta expresia raportului de transformare k_u

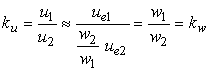(2.13)

unde se considera u , u₂ si u_e nenule, iar k_w este raportul numerelor de spire ale infasurarilor.