s, dupa sensul pe care il are, reprezinta un efect de intindere sau de compresiune iar tensiunea tangentiala t, are un efect de forfecare sau de lunecare.

e si reprezinta raportul dintre deformatia liniara a corpului, Dl si lungimea initiala l a acestuia: . Marimea e este o marime adimensionala si se exprima procentual.

g cu care se modifica unghiul drept al elementului de volum care apartine corpului supus deformarii. Se masoara in radiani. Lungirea specifica si lunecarea specifica sunt marimi fundamentale in studiul deformatiilor.

1.3. Relatii intre tensiuni si deformatii. Legea lui Hooke

e ( 1)

si arata ca, pana la limita de proportionalitate, lungirile specifice sunt proportionale cu eforturile. Relatia (1) reprezinta legea lui Hooke si este legea fundamentala a teoriei elasticitatii. Constanta E din legea lui Hooke poarta denumirea de modul de elasticitate longitudinala (modulul lui Young). Avand in vedere faptul ca e este o marime adimensionala, din relatia (1) rezulta ca unitatea de masura pentru E este aceeasi ca si pentru efortul unitar. Valorile uzuale ale constantei E pentru otel sunt 2,1 10⁶ daN/cm

s_p. Punctul B din diagrama corespunde limitei de elasticitate s_e, adica punctului pana la care materialul este perfect elastic.

s_{c ,} corespunzatoare ordonatei punctului C din diagrama, este valoarea efortului unitar la care materialul din care este confectionata epruveta de incercat incepe sa curga. Deformatiile inregistreaza o crestere semnificativa la o tensiune aproximativ constanta. Fenomenul poarta denumirea de curgere aparenta a materialului.

unde G este o constanta, si reprezinta modulul de elasticitate transversala a materialului care se incearca. Valorile uzuale ale constantei G pentru otel sunt 8 10⁵ daN/cm

LA SISTEME PLANE STATIC DETERMINATE

Forta axiala N intr-o sectiune a unei bare este egala cu suma algebrica a proiectiilor pe axa barei a tuturor fortelor exterioare, inclusiv reactiunile, care actioneaza asupra partii situate la stanga sectiunii sau a celor din dreapta, cu semn schimbat.

Forta taietoare T intr-o sectiune este egala cu suma algebrica a proiectiilor pe normala la axa barei a tuturor fortelor exterioare, inclusiv reactiunile, care actioneaza asupra barei la stanga sectiunii sau a celor din dreapta, cu sensuri schimbate.

Momentul incovoietor M intr-o sectiune este egal cu suma algebrica a momentelor tuturor fortelor exterioare care actioneaza la stanga sectiunii, calculate in raport cu centrul de greutate al sectiunii sau a celor din dreapta, cu semn schimbat.

un reazem simplu (o necunoscuta) plus o articulatie (doua necunoscute)

o incastrare (trei necunoscute)

Ø Momentul incovoietor este conventional pozitiv cand produce lungirea partii inferioare a barei si scurtarea celei superioare.

Relatii diferentiale intre eforturi la bare drepte

Folosind figura 13 se calculeaza:

GG₁ = 10a – 7,051a = 949a

GG₂ = 10,5a – 7,051a = 3,449a

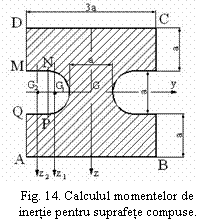Rezulta I_z = 2455,178a⁴

Tabelul 2 Valoarea coeficientului k pentru diverse profile de sectiuni

d=59,7 mm	a=52,9 mm	I18
A=28 cm²	A= 28 cm²	A= 27,9 cm²
		W_y = 161 cm³
k 6 cm	k 1 cm	k

5. INTINDERE SI COMPRESIUNE

5.1. Definitii. Relatii de calcul

O bara dreapta este solicitata la rasucire daca in sectiunile de capat ale barei sunt aplicate doua cupluri concentrate de moment M_t, egale in modul si orientate in sens invers; vectorii moment ai acestor cupluri sunt aplicati in centrele de greutate ale sectiunilor de capat, normal pe aceste sectiuni si orientati in sens invers.

Solicitarea de rasucire este produsa de forte care nu intalnesc axa barei, respectiv nu sunt paralele cu ea.

In acest capitol, se vor avea in vedere numai barele drepte de sectiune circulara sau inelara, pentru care studiul solicitarii de rasucire este mai simplu; barele cu alte forme de sectiune, de exemplu sectiune dreptunghiulara, se deplaseaza in timpul rasucirii, fapt care conduce la un calcul mai complicat.

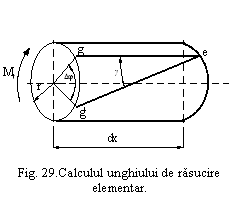Sub actiunea celor doua cupluri egale si direct opuse bara solicitata la rasucire se deformeaza; sectiunile barei se rotesc in jurul axei sale cu un unghi (fig.28). Elementul se afla intr-o stare de forfecare pura, astfel ca, in oricare sectiune a barei apar, in punctele situate pe sectiunea transversala, tensiuni tangentiale perpendiculare pe razele punctelor respective.

Se considera un element de bara din partea centrala r < R, de lungime dx, ale carui fete extreme se rotesc cu unghiul g (fig. 29)

Din considerente de deformatii se poate scrie:

arc (gg g dx = r dj

de unde

S-a notat cu q unghiul de rasucire specifica (unghiul cu care se rasucesc una fata de alta doua sectiuni transversale situate la distanta egala cu o unitate de lungime.

Folosind relatiile care rezulta din geometria deformarii impreuna cu legea lui Hooke pentru rasucire ( = G · g ), rezulta ca tensiunile tangentiale sunt repartizate liniar pe razele sectiunii:

= G r

unde reprezinta rotirea specifica si G este modulul de elasticitate longitudinala al materialului.

Folosind relatia de echivalenta a momentelor in raport cu centrul sectiunii () se deduce relatia dintre efortul M_tsi tensiunea τ in orice punct al oricarei sectiuni a barei considerate:

avand valoarea maxima in puctul cel mai departat de centrul sectiunii, la r_max = R.

in care

(44)

este modulul de rezistenta polar al sectiunii barei; I_peste momentul de inertie polar al sectiunii barei si r raza sectiunii barei.

Relatia (43) este relatia fundamentala pentru solicitarea de torsiune si serveste la dimensionarea, verificarea sau determinarea momentului de rasucire capabil al barei.

Integrand rotirea specifica se poate calcula unghiul de rasucire cu care se rotesc una fata de cealalta, doua sectiuni ale barei situate la distanta l:

(45)

Relatia 43 se poate folosi pentru rezolvarea a trei categorii de probleme:

a)Probleme de dimensionare. Se determina modulul de rezistenta necesar:

(46)

b)Probleme de verificare. Se calculeaza tensiunea tangentiala efectiva si se compara cu tensiunea admisibila

(47)

c) Calculul momentului de rasucire capabil

(48)

In relatiile de mai sus, t_a este tensiunea tangentiala admisibila a materialului barei.

Pentru sectiuni uzuale, expresiile modulului de rezistenta polar sunt prezentate in continuare.

Sectiune circulara.Pentru o bara de sectiune circulara, avand diametrul d, modulul de rezistenta polar este:

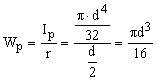(49)

Sectiune inelara. Pentru o bara de sectiune inelara, avand diametrul interior d si diametrul exterior D, modulul de rezistenta polar are expresia:

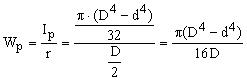(50)

Sectiunea inelara este mai avantajoasa decat cea circulara plina, deoarece, la aceeasi cantitate de material, are modulul de rezistenta polar mai mare si deci, poate suporta un moment de rasucire mai mare.

In mod obisnuit, la arborii, axele sau osiile de masini se cunoaste puterea P, transmisa de aceste organe de masini si turatia n. Pentru aceste cazuri, momentele de rasucire se calculeaza cu relatiile:

(51)