REGIMUL ELECTROCINETIC STATIONAR (REGIMUL CIRCUITELOR DE CURENT CONTINUU)

REGIMUL ELECTROCINETIC STAŢIONAR (REGIMUL CIRCUITELOR DE CURENT CONTINUU)

4.1. Definire, caracterizare, legi si teoreme specifice

Se numeste regim electrocinetic stationar, regimul circuitelor electrice parcurse de curent de conductie continuu, caracterizate local prin legea conductiei electrice:

pasive de circuit).

d. Teorema potentialului electric stationar (consecinta a legii inductiei electromagnetice);

,

cu consecintele acesteia:

-câmpul electric în conductoarele parcurse de curent electric stationar este de natura potentiala, ca si în regim electrostatic, deci provine dintr-un potential:

;

Fig. 4.2.1. Definirea sensurilor curentului de conductie

Fig. 4.2.2. Sensul conventional pozitiv al curentului si al laturii

Fig. 4.2.3. Sensul conventional pozitiv al t.e.m.

Fig. 4.2.4. Pila electrochimica Cu-Zn

Fig.4.2.5. sensul conventional (pozitiv) al t.e.m.

Fig. 4.2.6.Asocierile permise între curent si tensiune

Fig.4.2.7. Asocierea curentului si tensiunii în cadrul legii lui Ohm în cele doua conventii

Fig. 4.2.8. Câmp imprimat de acceleratie

Acestei forte îi corespunde un câmp electric imprimat;

.

Cum sarcina electrica este negativa (sarcina electronului), se poate scrie ca si rezulta:

.

Ca urmare, câmpul electric imprimat asociat fortei centrifuge este dirijat în sens opus acestei forte.

Fig. 4.2.9. Câmp imprimat termoelectric

Fig. 4.2.10. Pila galvanica

Fig. 4.2.11. Pila Leclanche

Caracteristicile pilei Leclanche sunt:

Fig. 4.2.12.Câmp imprimat voltaic

Surse ideale de curent continuu

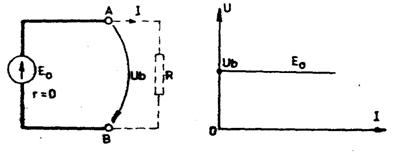
Fig.4.2.13. Generatorul ideal de tensiune

,

iar rezistenta interna a sursei ideale este nula( r = 0).

Fig.4.2.14.Generatorul real

,

caracteristica U(I) fiind cazatoare, ca în fig. 4.2.14. Aceasta caracteristica intersecteaza abscisa () în punctul M ,în care curentul ia valoarea de scurtcircuit:

Fig.4.2.15. Generatorul ideal de curent

Fig.4.2.16.Generatorul real

.

Mentiunea 1

Mentiunea 2

Fig.4.3.1. Circuit de c.c

O = L -( N -1)=L-N+1,

Fig.4.3.2. Circuitul simplu de curent continuu

.

Dezvoltând integrala se obtine:

,

Separând egalitatea în doua parti, pentru curba , respectiv pentru curba , se obtine:

.

,

.

Aceasta relatie reprezinta ecuatia laturilor generatoare, care contine o sursa de t.e.m. ,, având rezistenta interna r, si care are la borne tensiunea .

Sub alta forma, si anume , ecuatia laturii generatoare evidentiaza faptul ca tensiunea la bornele acestei laturi (a unei surse de c.c, în general) este egala cu t.e.m. a sursei de tensiune, mai putin caderea de tensiune interna pe sursa.

Se va scrie acum egalitatea corespunzatoare termenilor laturii din dreapta (curba C₂):

.

;

,

Fig.4.3.3. Ecuatia laturii receptoare active

Fig.4.3.4. Regula de la generatoare în doua variante: a si b.

În figura 4.3.6 se reprezinta cazul particular al unei laturi receptoare continând o sursa care se încarca (cazul încarcarii unui acumulator).

În acest caz (este vorba de ecuatia laturii receptoare) sensul t.e.m. este inversat (tensiune contraelectromotoare), conform ecuatiei:

În scopul rezolvarii circuitelor sau retelelor de curent continuu se utilizeaza mai multe teoreme si metode, între care cele mai importante vor fi prezentate în continuare. O importanta deosebita între acestea o are metoda teoremelor lui Kirchhoff, aplicabila în orice situatie, din aceasta derivând toate celelalte metode.

Fig.4.4.1. Nod independent de circuit

Teorema întâi a lui Kirchhoff este o consecinta directa a teoremei continuitatii liniilor de curent (aceasta fiind, la rândul ei, o consecinta directa a legii conservarii sarcinii electrice).

Curentii care ies din nod se considera pozitivi (au acelasi sens cu normala pozitiva la suprafata închisa ), iar cei care intra în nod - negativi.

Prima teorema a lui Kirchhoff se aplica în (N-1) noduri ale retelei, unde (N-1) este numarul nodurilor independente.

Fig. 4.4.2. Ochi fundamental de circuit

Se traseaza curba de integrare de-a lungul laturilor unui ochi de circuit si i se atribuie acesteia un sens de parcurs, care reprezinta sensul de referinta pentru tensiunile laturilor ochiului.

Aplicând teorema potentialului electric stationar pe curba se poate scrie:

,

(V_A-V_B) + (V_B-V_C) + .......+ (V_F-V_A) = 0.

,

,

,

.

,

a. caracterizarea topologica a circuitului/retelei, respectiv stabilirea numarului de laturi (L) , noduri independente (N) si ochiuri fundamentale (0 = L - N+1);

b. adoptarea (în mod arbitrar) de sensuri de parcurgere a ochiurilor (sensuri de referinta), precum si de sensuri conventionale (pozitive) pentru t.e.m., curenti si tensiuni;

c. scrierea ecuatiilor corespunzatoare teoremelor lui Kirchhof, si anume:

(N-1) ecuatii, pentru teorema I;

O ecuatii, pentru teorema a II-a.

Numarul total al ecuatiilor sistemului va fi egal cu L, respectiv cu numarul curentilor din laturi;

d. rezolvarea sistemului de ecuatii algebrice liniare, respectiv determinarea curentilor din laturile circuitului.

Pe baza curentilor se pot determina apoi tensiunile la bornele laturilor, utilizând, pentru fiecare latura în parte , ecuatia laturii, scrisa fie dupa conventia de la generatoare, fie dupa cea de la receptoare.

Daca rezulta curenti negativi, se schimba sensurile acestora pe laturile respective ale circuitului.

e. verificarea rezultatelor obtinute, în care scop se pot utiliza ca metode:

,

Fig.4.4.3

N = 4; L = 6; 0 = L - N + 1 = 3 .

Se aleg sensuri de parcurs arbitrare pe ochiurile O_I, O_II, O_III (sensuri de referinta), precum si sensuri conventionale pentru curentii laturilor (I_1,.....I₆).

Se scriu matricele:

Se aplica prima teorema:

Se aplica a doua teorema:

Cele doua matrice conduc la sistemul :

.

;

Se vede ca si, ca urmare, rezultatele obtinute sunt corecte.

4.4.3. Teorema conservarii puterilor

Numita si teorema bilantului de puteri, aceasta teorema se enunta altfel:

Suma algebrica a puterilor primite si cedate de toate laturile unei retele electrice izolate ( autonome) pe la borne este nula (fig. 4.4.4).

Expresia teoremei este data de relatia:

Teorema conservarii puterilor este o consecinta a primei teoreme a lui Kirchhoff. Astfel, daca expresia corespunzatoare primei teoreme a lui Kirchhoff se înmulteste cu potentialul nodului pentru care este scrisa teorema si se sumeaza expresia obtinuta pentru toate nodurile retelei, se obtine:

Curentul din fiecare latura intervine în aceasta suma de doua ori: odata cu semnul (+), pentru nodul din care iese (b) si odata cu semnul (-), pentru nodul în care intra (c).

Regrupând termenii, se poate scrie:

,

(4.4.15. a)

.

(4.4.15.b.)

( conform teoremei conservarii).

Se obtine:

4.4.4. Teorema transferului maxim de putere pe la borne

Un generator de t.e.m. E, având interna R_g, transfera o putere maxima P_S sarcinii R_S ,cu conditia ca rezistenta R_S sa fie egala cu R_g; randamentul transferului maxim de putere este de 50%().

Fie circuitul din fig. 4.4.5., în care rezistenta de sarcina R_S este variabila.

Puterea primita de la receptor pe la bornele AB este data de relatia:

.

,

.

Curba de variatie a puterii cerute de sarcina si a randamentului transmisiei la variatia rezistentei acesteia este aratata în fig. 4.4.6.

Puterea furnizata de sursa în acest caz devine:

.

În cazul transferului maxim de putere (R_g = R_S) se spune ca sarcina este adaptata la generator.

De exemplu o buna receptie din partea unui radioreceptor se asigura daca se realizeaza adaptarea între antena si aparat, respectiv daca impedanta antenei este egala cu impedanta de intrare a radioreceptorului.

În continuare sunt comentate doua exemple de transfer de putere, unul la randament maxim si altul la randament mai mare.

Exemplul 1

Fie : .

Rezulta: ; ;

(maxim).

Exemplul 2

Fie, acum: .

Puterea maxima care poate fi data de generator este ():

,

Fig.4.4.7. Dipol receptor pasiv

Nota:

Un dipol este un circuit cu doua borne de acces în exterior

Conexiunile rezistoarelor în circuitele electrice pot fi de tipul serie, paralel sau mixt.

; cum , facând echivalenta cu    schema (4.4.9) se obtine egalitatea:

;

.

Fig. 4.4.8. Conexiunea serie

Fig. 4.4.9. Schema echivalenta

.

Cum:

facând echivalenta schemei (4.4.10.a) cu (4.4.10.b) se obtine:

.

Evident, în cazul unei conexiuni mixte rezistenta totala va fi o combinatie a celor doua variante.

Ca aplicatii ale teoremelor rezistentelor echivalente se prezinta divizorul de tensiune si divizorul de curent.

Fig. 4.4.11. Divizor de tensiune

Se poate scrie:

Fig. 4.4.12 Divizorul de curent

Se poate scrie:

4.4.6.Metoda suprapunerii efectelor (superpozitiei)

Enuntul acestei metode( teoreme) este urmatorul: Intensitatea curentului electric din orice latura a unei retele electrice liniare, în care actioneaza mai multe surse, este suma algebrica a intensitatilor curentilor pe care i-ar stabili prin latura respectiva fiecare sursa, daca ar functiona singura în retea.

Metoda se aplica numai circuitelor (retelelor) liniare si poate fi exprimata prin relatia:

Pentru determinarea curentilor I_j din laturi se determina mai întâi curentii din laturile circuitelor modificate, rezultate prin descompunerea circuitului initial, care vor trebui sa contina numai câte o sursa, utilizând una din metodele de rezolvare cunoscute; dupa care, fiecare curent de latura se calculeaza sumând algebric curentii, prin aceeasi latura, din circuitele în care a fost descompusa reteaua data.

Aplicatie

Se da circuitul din figura 4.4.13 în care se cunosc valorile surselor E₁, E₂ si ale rezistoarelor R₁, R₂ si R₃. Se cere sa se determine valorile curentilor în cele trei cazuri, utilizând teorema superpozitiei.

Rezolvare

Circuitul initial a se poate considera, datorita proprietatii de liniaritate, ca fiind format printr-o suprapunere a doua circuite, b si c, în care se pastreaza, pe rând, câte o sursa.

În aceste conditii, expresiile curentilor devin:

Expresiile curentilor I_ij de mai sus s-au scris utilizând teorema divizorului de curent. Evident ca se pot folosi si alte metode pentru determinarea lor.

,

.

Din schema b rezulta:

,

; .

Fig. 4.4.15. Generatorul de tensiune echivalent

,

Fig. 4.4.16.Reteaua liniara

Teorema se demonstreaza pe baza teoremei precedente, observând ca:

Daca se împart atât numaratorul cât si numitorul cu ,se obtine:

a. Tranzistor bipolar

b. Generatorul de curent echivalent

; ; .

Schemele a si b sunt echivalente când tensiunile între noduri si curentii din noduri sunt aceiasi, respectiv puterile absorbite de cele doua subretele sunt identice.

Demonstratia teoremei se face presupunând bornele 1,2 si 3 izolate pe rând câte una, astfel încât dipolii ramasi sa aiba rezistentele echivalente, calculate între celelalte doua borne, egale pentru schemele în stea si triunghi.

; ; .

Demonstratia teoremei se face presupunând pe rând bornele scurtcircuitate doua câte doua si punând conditia ca rezistentele echivalente la conexiunea stea si triunghi pentru dipolii obtinuti sa fie egale.

4.4.9. Metoda curentilor de ochiuri (ciclici)

Metoda curentilor de ochiuri, numita si metoda curentilor ciclici (Maxwell) prezinta avantajul ca opereaza cu un numar mai mic de variabile fata de metoda teoremelor lui Kirchhoff si anume, cu O < L, unde O este numarul de ochiuri fundamentale ale retelei.

Marimile variabile în ecuatiile retelei vor fi în acest caz curentii de ochiuri (ciclici) - curenti fictivi atribuiti ochiurilor fundamentale, astfel încât curentul din fiecare latura k sa fie egal cu suma algebrica a curentilor ciclici care parcurg latura respectiva:

Sumarea se efectueaza pentru toti curentii ochiurilor q carora le apartine latura k.

Matematic, relatia (4.4.39) reprezinta o schimbare liniara de variabila de la L necunoscute (curentii laturilor) la O necunoscute (curentii fictivi atribuiti ochiurilor fundamentale). Acest lucru este posibil numai în conditiile asigurarii compatibilitatii cu sistemul ecuatiilor lui Kirchhoff. Astfel cele (N-1) ecuatii date de prima teorema a lui Kirchhoff sunt identic satisfacute, deoarece fiecare curent ciclic intra si iese odata în fiecare nod, aducând o contributie nula la curentul total prin suprafata închisa care cuprinde nodul:

Restul de O variabile vor fi univoc determinate de cele L - (N-1) = O ecuatii ramase, date de cea de-a doua teorema a lui Kirchhoff:

, conform relatiei (4.4.39).

Ordonând relatia (4.4.41) dupa curenti, se mai poate scrie:

.

Prin rezolvarea sistemului (4.4.43) se obtin curentii de ochiuri (). Utilizând transformarea liniara (4.4.39) se calculeaza apoi curentii de laturi ().

Etapele care trebuie parcurse la rezolvarea unei retele de c.c. prin aplicarea acestei metode sunt:

,

.

Matricea este de forma:

, fiind o matrice vector-coloana.

Prin rezolvarea sistemului (4.4.44) se obtine:

.

Curentii reali din laturile retelei se determina cu relatia:

Se aleg sensurile curentilor ciclici din ochiurile fundamentale ale relatiei.

Se formeaza matricele - de apartenenta a laturilor la ochiuri ( matricea de conexiune a retelei) si - transpusa acesteia.

Se formeaza matricele si .

Se calculeaza matricele si , cu relatiile (4.4.46) si (4.4.47).

Se calculeaza matricea inversa .

Se calculeaza matricea .

Se calculeaza matricea .

Se verifica rezultatele. În acest scop se poate utiliza, de pilda, teorema bilantului puterilor sub forma matriceala:

.

Fig.4.4.18. Aplicatie

Rezolvare

Se aleg sensurile indicate pe figura pentru curentii ciclici .

Se formeaza matricea de conexiune si transpusa acesteia:

; ;

; .

Ca urmare, curentii ciclici pot fi calculati cu matricea:

Curentii din laturi sunt:

Verificare

Se vede ca se verifica relatia de bilant:

4.4.10. Metoda potentialelor de/la noduri

În cazul metodei potentialelor de noduri se opereaza cu (N-1) variabile, mai putine fata de cele utilizate în cazul metodei curentilor de ochiuri , respectiv, al metodei teoremelor lui Kirchhoff:

(N-1) < 0 < L.

Noile variabile sunt potentialele nodurilor independente sau diferentele de potential dintre fiecare nod al retelei si un nod (al N-lea), ales arbitrar ca referinta (potential de referinta), considerat în mod obisnuit ca fiind legat la pamânt (V_N = 0).

Fie latura de circuit din figura 4.4.19, apartinând nodurilor (b) si (c) si nodul N al retelei, cu rol de referinta. Conform primei teoreme a lui Kirchhoff se poate scrie pentru nodul (b):

Ecuatia de functionare a laturii k este:

.

Se noteaza curentul de scurtcircuit al laturii k, având semnul (+) când intra într-un nod al laturii (nodul c); evident, si au acelasi sens prin latura k, în caz contrar semnele de mai sus se inverseaza.

Ca urmare:

Înlocuind pe în ecuatia corespunzatoare primei teoreme a lui Kirchhoff, se poate scrie:

.

Tensiunea , la bornele laturii k, este data de diferenta de preferential dintre cele doua noduri, b si c :

, respectiv .

Rezulta ca cele () variabile cautate (potentialele de noduri) vor fi univoc determinate de cele () ecuatii ramase, date de teorema I.

În aceste conditii, sistemul de ecuatii (4.4.56) devine:

, ,

Algoritmul aplicarii metodei este urmatorul:

Se aleg nodurile independente () si nodul de referinta, N, pentru care se scriu ecuatiile potentialelor de noduri.

Se calculeaza conductantele laturilor ().

Se calculeaza conductantele proprii si de cuplaj si curentii de scurtcircuit injectati în noduri ().

Se scrie sistemul de ecuatii al potentialelor si se rezolva în raport cu acestea.

Se calculeaza tensiunile la bornele laturilor:

Se calculeaza curentii din laturi, pornind de la ecuatiile laturilor. De exemplu, în cazul utilizarii conventiei de la receptoare se poate scrie:

,

Fig. 4.4.20.Retea liniara de c.c.

Sa se calculeze curentii cu ajutorul metodei potentialelor de noduri si sa se verifice rezultatele.

Rezolvare

Se alege arbitrar nodul (4) ca referinta (V₄ = 0), respectiv se considera acesta legat la pamânt.

Se calculeaza conductantele proprii si de cuplaj ale laturilor si curentii de scurtcircuit din nodurile retelei:

Curentii de scurtcircuit injectati în noduri sunt:

Se scrie sistemul de ecuatii în potentiale si se rezolva:

Înlocuind valorile conductantelor si curentilor se obtine:

; ; .

Se calculeaza curentii din laturi:

Curentul va avea semnul opus celui ales arbitrar( initial), respectiv semnul sagetii punctate.

Curentul va avea de asemenea sens opus celui ales initial, motiv pentru care i se va schimba sensul pe schema electrica (sageata punctata). Se vede ca în acest caz curentul nu va mai avea acelasi sens cu , deci sursa se încarca , respectiv absoarbe energie din retea.

Verificare:

Se vede ca: .

Nota

La calculul lui termenul se scade, deoarece sursa , asa cum s-a aratat, absoarbe energie de la retea în loc sa-i cedeze energie acesteia (are semnul opus lui )

4.4.11. Alte teoreme/ metode : metoda reciprocitatii, metoda compensatiei

.

Pentru demonstratie se considera o retea liniara având o singura latura activa (k), sursa fiind apoi mutata în latura (j).

Daca se scriu ecuatiile teoremelor lui Kirchhoff pentru cele doua retele, cum , se obtine usor relatia (4.4.60).

Aplicatie

Se da circuitul din fig. (4.4.22) cu valorile parametrilor indicate pe figura. Sa se aplice teorema reciprocitatii.

Se vede ca :

Fig. 4.4.23. Latura de retea liniara

Demonstratie

În cazul figurii a se poate scrie , conform legii lui Ohm. În cazul figurii b, din ecuatia laturii, scrisa utilizând, de exemplu, conventia de la receptoare, se obtine . Cum , rezulta ca ecuatia laturii ramâne neschimbata: , iar teorema este demonstrata.

4.5. Circuite neliniare de curent continuu

Circuitele neliniare de c.c. sunt circuite care contin elemente (rezistente) neliniare, respectiv dispozitive a caror rezistenta depinde continuu de curent sau tensiunea aplicata la borne si, ca urmare, caracteristica nu mai este o dreapta (este neliniara).Ca urmare acestor elemente (si circuite) nu li se mai poate aplica legea lui Ohm.

În continuare se prezinta câteva elemente neliniare tipice de circuit.

Fig. 4.5.1. Caracteristica de sarcina a lampii

Fig. 4.5.2. Caracteristica de sarcina a termistorului

Termistorul se utilizeaza în tehnica frecventelor înalte ca stabilizator de tensiune sau de curent, precum si ca circuit de protectie la suprasarcina (supracurent) sau la temperatura.

.

Rezistorul cu tirit se utilizeaza ca descarcator la protectia instalatiilor de înalta tensiune.

Fig. 4.5.4. Caracteristica de sarcina a tubului

e) Arcul electric

Este un proces specific sudurii electrice, cuptoarelor electrice cu arc, taierii electrice a metalelor, lampilor cu descarcari în arc (vezi pct. d), lampilor cu raze ultraviolete (fig. 4.5.5). La alimentarea cu tensiune constanta functionarea arcului electric este stabila numai daca se conecteaza în serie o rezistenta aditionala de protectie.

f) Redresorul cu semiconductoare (Se, Ge, Si)

Acest element neliniar se caracterizeaza printr-o conductanta mare într-un sens (sensul direct) si una foarte mica în sens contrar (fig. 4.5.6).

Redresoarele cu semiconductoare se utilizeaza pe larg în Electronica si în Electronica de putere (dioda, dioda de putere).

Rezistenta statica a diodei pentru un punct de functionare M este:

.

În cele doua relatii k este raportul scarilor grafice ale tensiunii (V/cm) si curentului (A/cm).

Fig. 4.5.7.Rezistenta statica si dinamica

Daca punctul de functionare al unui rezistor neliniar este pe portiunea coborâtoare a caracteristicii tensiune - curent (cazul unui arc electric), se spune ca rezistenta este negativa.

, b = 1,2,....,N-1;

, p = 1,2,....,O,

.

La rezolvarea circuitelor cu elemente neliniare se iau în consideratie atât ecuatiile corespunzatoare teoremei a doua a lui Kirchhoff, cât si caracteristicile elementelor neliniare, fie sub forma analitica, fie, mai ales, sub forma grafo-analitica.

Aplicatii

1. Sa se calculeze curentul de regim nominal al circuitului din figura (4.5.8), constituit prin conectarea în serie a doua rezistoare, unul liniar si altul neliniar. Se cunosc: R, E si caracteristica U(I) a elementului neliniar.

Rezolvare

Se utilizeaza metoda grafo -analitica (fig. 4.5.9). Ecuatia circuitului este , iar solutia ecuatiei (curentul I) este data de punctul de intersectie al celor doua curbe:

2. Sa se determine curentul printr-un circuit format prin conectarea în serie a doua circuite neliniare de tip rezistor (fig. 4.5.10). Se cunosc: ; ; .

Rezolvare

Se traseaza caracteristicile si si se aduna grafic, punct cu punct, cele doua tensiuni. Se obtine . Cunoscând valoarea tensiunii , se calculeaza curentul corespunzator acesteia (fig. 4.5.11), ducând o paralela la abscisa prin punctul de tensiune , pâna la intersectia M cu caracteristica . Curentul corespunzator ordonatei prin punctul M este cel cautat.

Nota

Termistoarele utilizate în receptoarele TV sunt rezistente cu coeficient de temperatura negativa (R scade cu cresterea temperaturii) si de valori ridicate. Sunt confectionate din oxizi de fier aliati cu Cr, Mg, Co, Ni si au rezistente cuprinse între 300 si 600 la temperatura de 20⁰C.