ALTE DOCUMENTE |
REGIMURILE STAŢIONARE DE FUNCŢIONARE ALE TRANSFORMATOARELOR MONOFAZATE
Un transformator alimentat de la o sursa de putere infinita, respectiv cu impedanta interna nula, se caracterizeaza prin valoare a tensiunii de alimentare independenta de nivelul de īncarcare īn sarcina.
Conform teoremei lui Thevenin, curentul secundar raportat corespunzator unei sarcini oarecare, definita prin impedanta raportata Z' , are expresia:

unde ![]() este tensiunea la
bornele secundare, raportata la primar, atunci cānd transformatorul
functioneaza īn gol, iar Z'sc este impedanta
sa īn raport cu bornele secundare atunci cānd bornele primare sunt
scurtcircuitate, respectiv impedanta de scurtcircuit a transformatorului
cu īnfasurarea primara raportata la secundar. Se
observa astfel ca curentul de sarcina I2 poate fi
īntotdeauna evaluat daca se cunoaste comportarea transformatorului īn
doua regimuri particulare, cel de gol si ce īn scurtcircuit.
este tensiunea la
bornele secundare, raportata la primar, atunci cānd transformatorul
functioneaza īn gol, iar Z'sc este impedanta
sa īn raport cu bornele secundare atunci cānd bornele primare sunt
scurtcircuitate, respectiv impedanta de scurtcircuit a transformatorului
cu īnfasurarea primara raportata la secundar. Se
observa astfel ca curentul de sarcina I2 poate fi
īntotdeauna evaluat daca se cunoaste comportarea transformatorului īn
doua regimuri particulare, cel de gol si ce īn scurtcircuit.
3.4.1. Functionarea īn gol
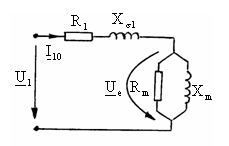
Schema echivalenta a transformatorului la functionarea īn gol, respectiv pentru I2 = I'2 = 0 este aceea din figura 3.23. Se presupune ca transformatorul este alimentat īn conditii nominale, U1n , fn . Īn acest regim curentul primar are o valoare foarte redusa īn 424j92e raport cu valoarea sa nominala,
![]()
ceea ce īnseamna ca pierderile de putere activa īn īnfasurarea primara sunt nesemnificative īn raport cu valoarea corespunzatoare regimului nominal,
![]()
Pierderile de putere activa īn miezul magnetic au practic valoare corespunzatoare regimului de sarcina nominala; aceste pierderi sunt proportionale cu patratul fluxului magnetic, care are o valoare practic constanta, independenta de regimul de sarcina.
Cum la functionarea īn sarcina nominala cele doua categorii de pierderi, īn īnfasurari si īn miez, au valori comparabile, rezulta ca puterea absorbita de transformator
Fig. 3.23 la functionarea īn gol este cu foarte buna aproximatie egala
cu pierderile magnetice īn regimul nominal, Pmn ,
![]()
Caderea de tensiune pe impedanta R1 + jXs , constituita de parametri īnfasurarii primare, fig. 3.23, este nesemnificativa īn raport cu tensiunea electromotoare Ue ; aceasta impedanta are valorii nesemnificative īn raport cu impedanta ramurii transversale a schemei echivalente, formata din Rm īn paralel cu Xm . Īn aceste conditii,
![]()
si daca tensiunea de alimentare u1 este sinusoidala, fluxul magnetic principal īn miez j, respectiv inductia magnetica au de asemenea o variatie sinusoidala.
Aplicarea legii circuitului magnetic īn lungul unei linii de cāmp īn miez,
![]()
evidentiaza faptul ca variatia īn timp a curentului de mers īn gol, i10(t), reproduce la alta scara dependenta HFe (t). Curba H(t) , respectiv variatia īn timp a curentului de mers īn gol i10(t), se construieste pe baza ciclului dinamic de magnetizare B(H), fig.3.24, si a dependentei sinusoidale B(t) a inductiei īn miez. Se observa pe de o parte ca curba curentului de mers īn gol este nesinusoidala si pe de alta parte ca fundamentala curentului este defazata īnaintea fluxului magnetic īn miez, ambele rezultate fiind datorate fenomenului de histerezis magnetic. Curentul de mers īn gol este defazat īn raport cu tensiunea de alimentare cu mai putin de 90 ; acest defazaj va fi si mai redus īn conditiile luarii īn considerare si a celei de-a doua componente a pierderilor īn miez, cele prin curenti turbionari.

3.4.2. Functionarea īn scurtcircuit
Regimul propriu-zis de scurtcircuit al unui transformator alimentat cu tensiunea nominala, respectiv acela īn care bornele īnfasurarii secundare se scurtcircuiteaza, este un regim de avarie. Curentul absorbit īn acest caz,
![]()
are valori extrem de mari īn raport cu curentul nominal, I1sc = (10.30) I1n.
Se
defineste tensiunea de scurtcircuit, ![]() , sau procentual īn raport cu tensiunea nominala,
, sau procentual īn raport cu tensiunea nominala,
![]()
ca fiind tensiunea ce trebuie aplicata primarului, atunci cānd secundarul este scurtcircuitat, astfel īncāt curentul absorbit sa aiba valoarea nominala. Īn mod uzual tensiunea de scurtcircuit are valori īn gama usc = (3.10)%. Īn functie de aceasta marime, curentul de scurtcircuit are expresia:
![]()
din care rezulta ca marimea 100/usc[%] arata de cāte ori este mai mare curentul de scurtcircuit īn raport cu curentul nominal.
Marimea:
![]()
este componenta activa a tensiunii de scurtcircuit, care este proportionala cu pierderile Joule īn īnfasurari la sarcina nominala. Marimea:
![]()
este componenta reactiva a tensiunii de scurtcircuit.
Īncercarea experimentala avānd ca scop evaluarea tensiunii de scurtcircuit a unui transformator se numeste īncercare īn scurtcircuit. Īn acest caz tensiunea de alimentare are valori reduse, reprezintānd (3.10)% din tensiunea nominala. Ca urmare, pierderile īn miezul magnetic, care sunt proportionale cu patratul tensiunii, reprezinta (0,09.1)% din valoarea lor nominala. Īn schimb, deoarece curentii prin īnfasurari au valorile nominale, pierderile īn īnfasurari sunt cele nominale. Cum pierderile nominale īn miez si īn īnfasurari au valori comparabile, rezulta ca puterea absorbita de transformator la īncercarea īn scurtcircuit este cu o foarte buna aproximatie egala cu pierderile nominale īn īnfasurari,
![]()
3.4.3. Functionarea īn sarcina. Bilantul puterilor. Caracteristica
randamentului. Caracteristica externa
Studiul functionarii īn sarcina īn conditiile alimentarii nominale are ca scop determinarea anumitor caracteristici de functionare ale transformatorului. Dependenta tensiunii secundare īn functie de curentul de sarcina, U2(I2) , se numeste caracteristica externa.; o alta caracteristica importanta este dependenta randamentului transformatorului īn functie de gradul sau de īncarcare īn sarcina.
a) Bilantul puterilor si caracteristica randamentului. Multiplicānd cele doua ecuatii de tensiuni:
![]()
![]()
cu marimile ![]() respectiv
respectiv ![]() si adunāndu-le se
obtine relatia:
si adunāndu-le se
obtine relatia:
![]()
unde ![]() ; Marimile S1 , S2
sunt puterile aparente complexe absorbita de primar, respectiv
debitata de secundar, iar P1 , P2 , Q1 ,
Q2 puterile activa
si reactiva corespondente. Ultimul termen,
; Marimile S1 , S2
sunt puterile aparente complexe absorbita de primar, respectiv
debitata de secundar, iar P1 , P2 , Q1 ,
Q2 puterile activa
si reactiva corespondente. Ultimul termen,
![]()
este puterea aparenta asociata miezului magnetic, avānd ca parte activa pierderile de putere Pm īn miez si ca parte reactiva puterea reactiva de magnetizare a miezului Qm.
Notānd cu :
Pj1 = R1I12 , pierderile Joule īn īnfasurarea primara,
Pj2 = R'2I'22 = R2I2, pierderile Joule īn īnfasurarea sedcundara,
Qs = Xs I12 , puterea reactiva corespunzatoare cāmpului de dispersie al
īnfasurarii primare,
Qs = X's I'22 = Xs I22, puterea reactiva corespunzatoare cāmpului de
dispersie al īnfasurarii secundare,
rezulta egalitatile:
![]()
![]()
Aceste doua relatii caracterizeaza bilantul puterilor activa si reactiva īn transformator. Expresia grafica a acestui bilant este īnfatisata īn figura 3.25.
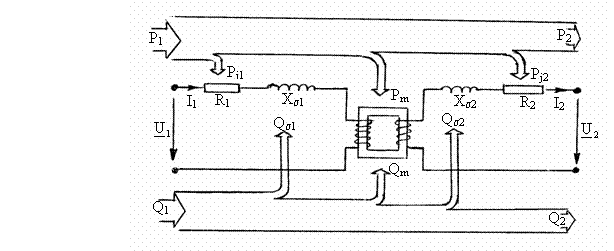 Fig. 3.25
Fig. 3.25Randamentul este raportul dintre puterea activa debitata si puterea activa absorbita,
![]()
Fie parametrul care exprima gradul de īncarcare īn sarcina:
![]()
Suma pierderilor Joule īn īnfasurari poate fi exprimata sub forma:
![]()
unde Pjn sunt pierderile nominale īn īnfasurari.
Functionānd sub tensiunea nominala, pierderile īn miez au valoarea nominala, Pm = Pmn, fiind evident independente de gradul de īncarcare īn sarcina. Deoarece U2I2 = U2n bI2n = bSn, expresia randamentului devine:
![]() ,
,
 ceea ce
īnseamna ca randamentul depinde doar de gradul de īncarcare īn
sarcina b si de factorul
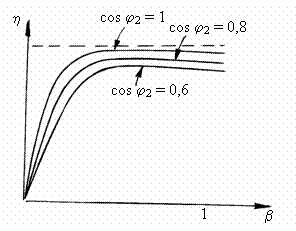
de putere al sarcinii cos j . Dependenta
randamentului īn functie de gradul de īncarcare īn sarcina
pentru valori cos j date este reprezentata
grafic īn figura 3.26. Pentru orice valoare b, valoarea randamentului
este cu atāt mai mica cu cāt sarcina este mai reactiva, adica
are un factor de putere cos j mai mic.
ceea ce
īnseamna ca randamentul depinde doar de gradul de īncarcare īn
sarcina b si de factorul
de putere al sarcinii cos j . Dependenta
randamentului īn functie de gradul de īncarcare īn sarcina
pentru valori cos j date este reprezentata
grafic īn figura 3.26. Pentru orice valoare b, valoarea randamentului
este cu atāt mai mica cu cāt sarcina este mai reactiva, adica
are un factor de putere cos j mai mic.
Pentru
o valoare data a factorului de putere al sarcinii, curba h b) are un maxim a carui
abscisa rezulta ca solutie a ecuatiei ![]() si are valoarea:
si are valoarea:

_files\image071.gif) Ordonata
corespunzatoare este:
Ordonata
corespunzatoare este:
Fig. 3.26 ![]()
Cum īn exploatare factorul de īncarcare īn sarcina are īn mod uzual valori īn intervalul 0,3.0,6 , interval īn care trebuie sa se situeze bm, rezulta ca īn dimensionarea transformatoarelor este recomandabil ca pierderile nominale sa se afle īn raportul:
![]()
Aplicatie. Un transformator cu puterea nominala Sn = 1000 kVA are randamentul nominal, pentru b hn = 98%. stiind ca randamentul maxim corespunde gradului de īncarcare īn sarcina bm = 0,333 , sa se calculeze pierderile nominale si randamentul transformatorului la sarcina nominala si valoarea factorului de putere cos j
Solutie: Pentru b =1 si cos j = 1 rezulta relatia:
![]()
de
unde ![]() . Asociind acestei relatii egalitatea :
. Asociind acestei relatii egalitatea :
![]()
rezulta pierderile nominale īn īnfasurari:

Pierderile nominale īn miez au valoarea:
![]()
Pentru b = 1 si cos j = 0,8 rezulta valoarea randamentului:
![]()
b) Caracteristica externa exprima dependenta tensiunii secundare U2 īn functie de curentul I2 si de factorul de putere al sarcinii cos j īn conditiile alimentarii nominale U1n , fn. Fie variatia relativa a tensiunii secundare:

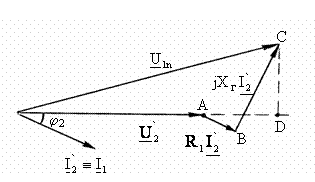
unde U20
si U2 sunt valorile tensiunii secundare īn gol si īn
sarcina. Pe baza diagramei fazoriale simplificate, fig. 3.27,
Fig. 3.27
se poate scrie succesiv:
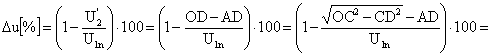

Folosind aproximatia 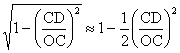 , rezulta
, rezulta  , respectiv,
, respectiv,
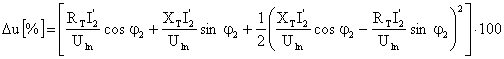
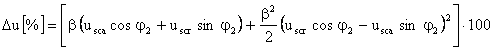

Caracteristica externa U2(I2, cos j ) rezulta din egalitatea:
![]()
si are pentru diverse valori ale facttorului de putere cos j alura din figura 3.28. Cu cāt sarcina are
Fig. 3.28 un caracter mai inductiv cu atāt
caracteristica externa este mai cazatoare. Īn schimb, o sarcina puternic capacitiva poate sa conduca la cresterea tensiunii secundare odata cu īncarcarea transformatorului īn sarcina.
3.5. TRANSFORMATOARE TRIFAZATE
3.5.1. Configuratia electromagnetica . Scheme si grupe de conexiuni
![]() ,
,
![]() ,
, ![]()
Prin sumare rezulta:
![]()
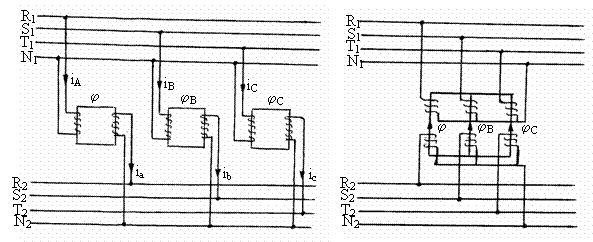
Fig. 3.29 Fig. 3.30
Cele trei transformatoare fiind identice rezulta iA + iB +iC = 0, respectiv cei trei curenti absorbiti formeaza un sistem trifazat simetric. Deoarece conform ipotezei uA + uB + uC = 0, rezulta jA jB jC = 0, respectiv ca cele trei fluxuri jA jB jC formeaza un sistem trifazat simetric. Rezulta astfel ca schema din figura 3.29 poate fi īnlocuita cu aceea din figura 3.30, care utilizeaza un transformator trifazat, īn care structura de miez magnetic cu trei coloane de tipul cu flux fortat asigura satisfacerea proprietatii jA jB jC = 0, valabila īn regimul simetric de tensiuni si curenti.
Īn cazul īn care sarcina este dezechilibrata, curentii debitati nu formeaza un sistem trifazat simetric, iar suma fluxurilor instantanee īn cele trei miezuri nu mai este nula,
![]()
Acelasi proprietate are loc daca alimentarea nu este trifazat simetrica.
 Daca miezul magnetic are trei
coloane, adica este de tipul cu flux fortat, fluxul rezultant j se va īnchide īn afara
miezului. Acest flux poate sa determine pierderi suplimentare de putere
importante prin curenti indusi īn structurile metalice ale
transformatorului. Daca se doreste ca acest flux sa se
īnchida printr-o structura de tipul miez magnetic cu pierderi reduse,
miezul magnetic este de tipul cu flux liber, cu cinci coloane, fig.3.31.
Daca miezul magnetic are trei
coloane, adica este de tipul cu flux fortat, fluxul rezultant j se va īnchide īn afara
miezului. Acest flux poate sa determine pierderi suplimentare de putere
importante prin curenti indusi īn structurile metalice ale
transformatorului. Daca se doreste ca acest flux sa se
īnchida printr-o structura de tipul miez magnetic cu pierderi reduse,
miezul magnetic este de tipul cu flux liber, cu cinci coloane, fig.3.31.
Fig. 3.31 Prin comparatie cu utilizarea a trei transformatoare monofazate,
transformatorul trifazat este o solutie mai economica, atāt prin cheltuielile de investitie, cāt si prin cele de exploatare.
Pe fiecare coloana a miezului se dispun de regula concentric īnfasurarile primara si secundara.
Notarea bornelor conform standardelor utilizeaza literele A, B, C, N pentru īnfasurarile de īnalta tensiune si a, b, c, n, pentru cele de joasa tensiune. Notarea bornelor prezinta o importanta apare atunci cānd apare problema cuplarii īn paralel a transformatoarelor.
b) Schemele de conexiuni ale celor trei faze ale
īnfasurarilor primare respectiv secundare pot fi stea
(simbol Y, y), triunghi (simbol D, d) sau zigzag (simbol Z, z). Conexiunea stea a
īnfasurarilor asigura doua sisteme de tensiuni: de
faza Uf , respectiv de linie Ul , cu relatia de
dependenta Ul = ![]() Uf . Intensitatea curentului īn cele trei
īnfasurari (faze) ale transformatorului are aceeasi valoare
cu curentul absorbit sau debitat din/īn linia la care transformatorul este
conectat, Il = If.
Uf . Intensitatea curentului īn cele trei
īnfasurari (faze) ale transformatorului are aceeasi valoare
cu curentul absorbit sau debitat din/īn linia la care transformatorul este
conectat, Il = If.
Presupunānd ca tensiunile induse īn cele trei īnfasurari de faza secundare sunt nesinusoidale descompunerea īn serie pune īn evidenta armonici de ordinul 3, 5, .:
![]()
![]()
![]()
Din expresia tensiunii de linie:
![]()
rezulta ca tensiunile de linie nu contin armonicele de ordinul 3, 9, 15. adica armonicile sinfazice.
Īn
cazul conexiunii triunghi tensiunile de faza ale celor trei
īnfasurari sunt egale cu tensiunile de linie ale retelei de
conectare, Uf = Ul, īn schimb curentii prin cele
trei faze sunt de ![]() ori mai mici decāt curentii absorbiti sau
debitati īn retelele de conectare If = Il/
ori mai mici decāt curentii absorbiti sau
debitati īn retelele de conectare If = Il/![]() .
.
Presupunānd ca, curentii de faza iab iax , ibc iby , ica icz sunt nesinusoidali, rezulta ca curentii de linie ia = iab - ica , ib = ibc - iab , ic = ica - ibc nu contin armonicele sinfazice.
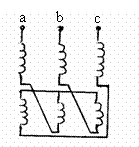 Conexiunea
zigzag, fig. 3.32, presupune ca īnfasurarea fiecarei
faze este formata din doua sectiuni identice plasate pe coloane
diferite ale miezului magnetic. De exemplu īnfasurarea fazei a se afla jumatate pe prima
coloana si cealalta jumatate pe cea de a doua coloana.
Relatiile de legatura īntre marimile de faza si
cele de linie sunt cele precizate la schema de conexiuni stea.
Conexiunea
zigzag, fig. 3.32, presupune ca īnfasurarea fiecarei
faze este formata din doua sectiuni identice plasate pe coloane
diferite ale miezului magnetic. De exemplu īnfasurarea fazei a se afla jumatate pe prima
coloana si cealalta jumatate pe cea de a doua coloana.
Relatiile de legatura īntre marimile de faza si
cele de linie sunt cele precizate la schema de conexiuni stea.
Daca Ua, Ub sunt fazorii tensiunilor de faza īn conexiunea stea, avānd modulul Ufy , se observa ca tensiunea de faza corespunzatoare conexiunii zigzag are valoarea:
Fig. 3.32 ![]()
mai mica de ![]() decāt īn cazul conexiunii stea.
decāt īn cazul conexiunii stea.
c) Grupe de conexiuni. Īn functie de schemele de conexiuni ale īnfasurarilor primare si secundare si de numerotarea bornelor, se pot obtine o multitudine de valori ale defazajului dintre tensiuni corespondente primara si secundara (de exemplu UAB, Uab , sau UAX, Uax ). Se poate usor verifica pentru un transformator Yy sau Dd ca acest defazaj este un multiplu de 30 , 2 x 30 , 4 x 30 , 6 x 30 , 8 x 30 , 10 x 30 ). Pentru un transformator Dy sau Yd acest defazaj este un multiplu impar de 30 (1 x 30 , 3 x 30 , 5 x 30 , 7 x 30 , 9 x 30 , 11 x 30
Īn sensul datelor nominale ale unui transformator, grupa de conexiuni este un simbol reprezentānd schemele de conexiuni ale primarului si secundarului si cifra care caracterizeaza defazajul dintre doua tensiuni primara si secundara corespondente, de exemplu Yy0, Dd6, Yd5, Yz11. Īn figura 3.33 sunt prezentate conexiunile si diagrama fazoriala a tensiunilor primare si secundare corespunzatoare grupelor de conexiuni Yy0, Yd5, Dz6.
Fig. 3.33
3.5.2. Functionarea transformatoarelor trifazate pe sarcini dezechilibrate
Sistemele trifazate de distributie alimenteaza īn mod frecvent si receptoare monofazate, care nu pot fi distribuite īntotdeauna pentru a asigura o īncarcare simetrica a celor trei faze. Astfel, transformatoarele trifazate pot ajunge sa functioneze īn regimuri asimetrice. Comportarea transformatoarelor īn astfel de regimuri depinde īn principal de constructia miezului si de schema de conexiuni ale īnfasurarilor.
Īn analiza comportarii transformatoarelor trifazate īn regimuri asimetrice se considera alimentarea trifazat simetrica si miezul magnetic este liniar, ceea ce īnseamna ca impedanta de magnetizare este constanta. Pentru simplitate, se considera ca cele īnfasurarile primara si secundara au acelasi numar de spire, w1 = w2.
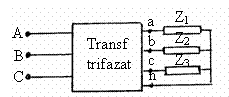 Problema fundamentala a
structurii din figura 3.34, īn care cele trei impedante de sarcina au
valori diferite Z1 Z2
Z3 (sarcina
trifazata dezechilibrata), este aceea de a determina curentii
primari si secundari si tensiunile secundare atunci cānd tensiunile
de alimentare UAB, UBC, UCA
formeaza un sistem trifazat simetric.
Problema fundamentala a
structurii din figura 3.34, īn care cele trei impedante de sarcina au
valori diferite Z1 Z2
Z3 (sarcina
trifazata dezechilibrata), este aceea de a determina curentii
primari si secundari si tensiunile secundare atunci cānd tensiunile
de alimentare UAB, UBC, UCA
formeaza un sistem trifazat simetric.
Cea mai generala abordare a acestei probleme utilizeaza metoda componentelor simetrice, conform careia sistemului nesimetric de curenti IA, IB, IC, fig. 3.35, i se asociaza componentele simetrice directa Id, inversa Ii si homopolara Ih si reciproc pe baza relatiilor:
Fig. 3.34
 Fig.
3.35 (de schimbat iB cu iC si iC cu
iB)
Fig.
3.35 (de schimbat iB cu iC si iC cu
iB)
 ,
,
unde ![]() .
.
Īn raport cu cele doua sisteme trifazate simetrice de curenti, direct si invers, transformatorul are aceeasi impedanta, anume impedanta de scurtcircuit,
Zd = Zi = ZT= RT + j XT
 Īn
raport cu sistemul de curenti de succesiune homopolara,
impedanta corespunzatoare, Zh = Rh + j Xh
, este parametrul asociat componentelor homopolare ale fluxului magnetic īn
cele trei faze. Aceste fluxuri sunt sinfazice si vor avea valori diferite
īn functie de tipul miezului. Astfel, īn cazul transformatorului cu trei
coloane, cu flux fortat, fluxul homopolar rezultant al celor trei coloane
se īnchide īn exteriorul miezului magnetic, pe o cale de reluctanta magnetica
mare, ceea ce face ca reactanta corespunzatoare Xh sa
aiba o valoare relativ redusa, fig. 3.36. Īn cazul transformatoarelor
trifazate cu cinci coloane, respectiv cu flux liber, fluxurile homopolare se
īnchid prin coloanele laterale,
Īn
raport cu sistemul de curenti de succesiune homopolara,
impedanta corespunzatoare, Zh = Rh + j Xh
, este parametrul asociat componentelor homopolare ale fluxului magnetic īn
cele trei faze. Aceste fluxuri sunt sinfazice si vor avea valori diferite
īn functie de tipul miezului. Astfel, īn cazul transformatorului cu trei
coloane, cu flux fortat, fluxul homopolar rezultant al celor trei coloane
se īnchide īn exteriorul miezului magnetic, pe o cale de reluctanta magnetica
mare, ceea ce face ca reactanta corespunzatoare Xh sa
aiba o valoare relativ redusa, fig. 3.36. Īn cazul transformatoarelor
trifazate cu cinci coloane, respectiv cu flux liber, fluxurile homopolare se
īnchid prin coloanele laterale,
Fig. 3.36 ceea ce face ca reactanta Xh sa
aiba o valoare mult mai mare.
Rezistenta homopolara Rh este parametrul corespunzator ansamblului pierderilor de putere īn partile metalice exterioare miezului la transformatorul cu flux fortat si al pierderilor Joule īn īnfasurarile conectate īn triunghi. Tensiunile electromotoare induse īn īnfasurarile celor trei faze sunt de sinfazice. Ca urmare, īn cazul īnfasurarilor conectate īn triunghi apare un curent de circulatie homopolar. Īn general, cu cāt puterea transformatorului este mai mare cu atāt rezistenta Rh este mai redusa īn raport cu reactanta Xh.
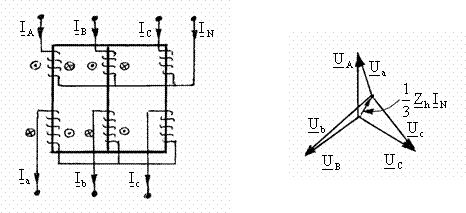
a) Calculul curentilor secundari si al tensiunilor secundare ale unui transformator Y0y ce debiteaza pe o sarcina dezechilibrata, fig. 3.37, alimentat cu tensiuni de faza simetrice. Aplicānd legea circuitului magnetic pe contururile celor doua ochiuri ale miezului magnetic, rezulta relatiile:
![]()
![]()
Fig. 3.37 Fig. 3.38
Conexiunile īnfasurarilor corespund relatiilor:

![]()
Aceste patru relatii determina univoc expresiile curentilor secundari īn functie de cei primari
![]()
Componentele simetrice asociate curentilor secundari sunt:
![]()
![]()
![]()
![]()
Componentele simetrice ale tensiunilor de alimentare UA, UB, UC (care formeaza un sistem trifazat simetric, ceea ce īnseamna ca UB = a2UA, UC = aUA) sunt
U1d
=![]() UA, U1i = 0, U1h = 0
UA, U1i = 0, U1h = 0
Rezulta expresiile componentelor simetrice ale tensiunilorsecundare:
![]()
Pe baza acestora, cele trei tensiuni de faza secundare rezulta:
![]()
![]()
![]()
![]() ,
,
![]()
![]()
Se
observa astfel ca tensiunile secundare nu mai formeaza un sistem
trifazat simetric, caderile de tensiune fiind influentate si de
impedanta homopolara Zh . Īn cazul neglijarii
caderilor de tensiune pe impedanta de scurtcircuit ZT
a transformatorului; tensiunile secundare difera de cele primare prin
termenul ![]() , iar diagrama de fazori a tensiunilor este
aceea din figura 3.38.
, iar diagrama de fazori a tensiunilor este
aceea din figura 3.38.
b) Comportarea la alimentarea unei sarcini monofazate.
b1) Īn cazul unui transformator cu schema de conexiuni Yy, fig. 3.39, avānd sarcina conectata īntre doua faze,
![]()
Prin aplicarea legii circuitului magnetic, la care se adauga relatia IA + IB + IC = 0, rezulta:
![]()
Īn aceasta schema, o sarcina monofazata conectata īntre doua faze se reflecta īn primar ca o sarcina dezechilibrata.

Fig. 3.39 Fig. 3.40
b2) Daca sarcina monofazata se conecteaza īntre o faza si nul a unui transformator Yy0, fig. 3.40, rezulta curentii absorbiti:
![]()
Solenatiile rezultante pe cele trei coloane ale transformatorului,
![]()
au acelasi sens si sunt īn faza. Īn cazul transformatoarele cu flux liber aceste solenatii produc fluxuri magnetice importante, care induc īn īnfasurarile de faza secundare tensiuni sinfazice. Aceste tensiuni deplaseaza originea sistemului tensiunilor de faza spre vārful corespunzator fazei īncarcate, asa īncāt tensiunea acestei faze se reduce si cresc celelalte doua tensiuni de faza. Din acest motiv nu este permisa īncarcarea īn sarcina nesimetrica a unui transformator cu flux liber, avānd schema de conexiuni Yy0.
Īn cazul transformatoarelor cu flux fortat, fluxurile sinfazice sunt mai reduse, deplasarea nulului este mai putin pronuntata, īn schimb aceste fluxuri pot produce pierderi importante de putere prin curenti indusi īn piesele metalice exterioare miezului magnetic.
b3) Īn cazul unui transformator cu conexiunea Yz, stea īn primar si zigzag īn secundar, fig. 3.41, avānd o sarcina monofazata conectata īntre faza a si nul, aplicarea legii circuitului magnetic conduce la relatiile:
![]() ,
, ![]()
Adaugānd relatia ![]() , se obtin curentii primari:
, se obtin curentii primari:
![]()
Sarcina monofazata din secundar se reflecta īn primar ca o sarcina conectata īntre doua faze, iar solenatiile rezultante pe cele trei coloane sunt nule.
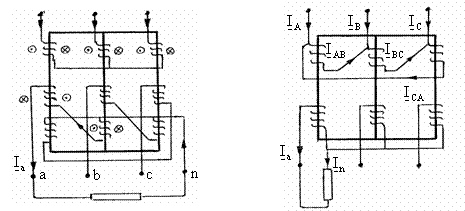
b4) Cazul unui transformator cu conexiune Dy0 , triunghi īn primar si stea īn secundar, fig. 3.42. Sunt valabile relatiile:
![]()
![]() ,
,
Prin exprimarea fluxurilor īn functie de solenatie si reluctanta Rm, aceeasi pentru toate coloanele, se obtine:
![]()
respectiv,
IAB + IBC + ICA = Ia.
Rezulta IAB = Ia ; IBC = 0 ; ICA = 0. Sarcina monofazata se reflecta īn primar ca o sarcina conectata īntre doua faze.
|