RUPEREA PRIN SOLICITARE LA OBOSEALA

3.1 Particularitati ale mecanismului ruperii

Pentru a se pastra integritatea unei structuri mecanice trebuie ca tensiunea maxima sa fie mai mica decat rezistenta la rupere a materialului din care se executa piesa.

Aceasta conditie nu este suficienta in totalitatea cazurilor datorita unor cauze complexe, ce contravin acestor observatii, din care pot fi redate :

v         tensiunea nu actioneaza intotdeauna dupa o singura directie, creandu-se astfel o stare biaxiala sau triaxiala de tensiune;

v         trebuie luate in consideratie defectele (fisurile) existente in material;

v         tensiunea poate actiona perioademai indelungate de timp;

v         tensiunea poate fi aplicata sau indepartata in mod periodic sau poate fi schimbat sensul de solicitare.

Ruperea se poate produce datorita actiunii repetate a unei incarcari numita si incarcare ciclica.

Procesul de initiere si de propagare a uneia sau mai multor fisuri, care conduce la ruperea elementelor de rezistenta, se numeste oboseala.

Analiza propagarii fisurii prin oboseala permite stabilirea unor momente de urmarire si control al evolutiei fisurii, respectiv eliminarea fisurilor periculoase din piesele sau structurile care sunt studiate.

La piesele solicitate in masini si utilaje, ruperea se produce la un numar mare de cicluri, fara deformatii plastice, sensibile la scara macroscopica. Deformatiile plastice apar la nivelul cristalelor prin lunecari de pachete de atomi. La solicitari alternante, daca lunecarile sunt limitate si materialele se ecruiseaza local suficient, lunecarea poate fi oprita, in sens contrar lunecarile din zonele cele mai solicitate progreseaza, se transforma in una sau mai multe fisuri vizibile cu ochiul liber, care se maresc, reduc continuu sectiunea pana cand aceasta devine insuficienta pentru a rezista fortelor aplicate, producandu-se ruperea piesei.

Ruperea prin oboseala este initiata in regimurile vulnerabile, in zone cu concentratori de tensiune ( crestaturi, variatii de sectiune, defecte, etc.) si este facilitata de zonele slabite ale microstructurii ( existenta unor incluziuni ) si de orientarea planelor de alunecare in graunti, daca este apropiata de cea a tensiunilor tangentiale maxime. Portiunea din sectiune in care fisura s-a propagat cu o viteza relativ mica este netezita datorita frecarilor mutuale exercitate pe fete, aceasta parte a sectiunii fiind denumita zona de oboseala.

Fig. 3.1

Suprafata dupa care s-a produs ruperea finala poarta denumirea de zona de rupere instantanee, si are un caracter rugos cristalin, figura 3.1

La scara microscopica, toate materialele sunt neomogene si anizotrope. In interiorul fiecarui graunte comportarea metalului este anizotropa datorita existentei planelor cristalografice, iar la trecerea limitei dintre doi graunti orientarea acestora se schimba. Neomogenitatea este datorata nu numai structurii granulare, dar si existentei golurilor si a incluziunilor de silicati si aluminiu din oteluri. Datorita neuniformitatii microstructurale, tensiunile sunt distribuite neuniform, in regiunile cele mai solicitate producandu-se initierea ruperii. La materialele ductile, in cristalele care au o orientare nefavorabila, fata de tensiunile aplicate, exista plane de alunecare. Acestea sunt portiuni in care apare o puternica deformati 919h76j e datorata miscarii tangentiale dintre planele cristalografice.

Pe unele dintre planele de alunecare, in interiorul cristalelor, se produc microfisuri care se unesc cu altele similare, obtinandu-se astfel o fisura a carei propagare determina ruperea materialului. Microfisura, de forma unui gol, se formeaza ca o suprafata libera in jurul unei incluziuni sau a unei particule, acolo unde tensiunea este suficient de mare pentru a rupe legaturile lor cu grauntii metalului de baza.

In ruperea ductila se produce marirea dimensiunii golului prin deformatie specifica plastica si unirea golurilor alaturate. Cresterea tensiunii hidrostatice (media aritmetica a celor trei tensiuni normale principale) favorizeaza formarea golurilor !n jurul particulelor de dimensiuni mai mari. Suprafata de rupere are un aspect fibros, iar deformatiile specifice plastice sunt reduse. Prin reducerea starii triaxiale de tensiune este favorizata formarea golurilor in jurul particulelor de dimensiuni mai mici si unirea lor datorita deformatiilor specifice plastice importante, planele de alunecare avand inclinarea orientata la aproximativ 45 fata de directia tensiunii tangentiale maxime. Suprafata de rupere in acest caz se numeste suprafata de forfecare, cu un aspect neted, lucios, figura 3.1. Ruperea ductila este insotita de deformatii plastice.

Ruperea prin clivaj este determinata de o propagare rapida a fisurii de-a lungul unor plane de alunecare cristalografice. Aceasta este caracteristica materialelor fragile si implica o rupere fara deformatii plastice.

Planele de rupere, in general, sunt plane cu densitate atomica mixta, cu legaturile cele mai slabe, fisura rezultata prin clivaj este orientata perpendicular pe directia tensiunii principale mixte.

Ruperea prin clivaj este favorizata de factori care determina cresterea limitei de curgere a materialului: scaderea temperaturii, starea triaxiala de solicitare, viteze mari de incarcare, prezenta radiatiilor, etc.

Ruperea intergranulara se produce in metale prin propagarea tensiunii de-a lungul frontierei dintre graunti. Pot exista mai multe situatii:

v     coroziune intergranulara;

v     precipitarea unei faze fragile la frontiera dintre doi graunti;

v     formarea de cavitati sau microfisuri la marginea grauntelui datorita temperaturii ridicate.

Ruperea prin oboseala se produce progresiv sub actiunea unor solicitari variabile, chiar daca tensiunea de intindere sau compresiune este mai mica decat limita de elasticitate a materialului. Tensiunile locale pot fi mai mari decat limita de curgere a materialului datorita concentrarii tensiunilor in jurul incluziunilor sau microfisurilor. In acest caz deformatiile plastice apar la nivel microstructural.

Ruperea prin oboseala este conditionata de trei factori:

v     tensiunea de intindere;

v     deformatiile plastice;

v     solicitari ciclice sau variabile.

Ruperea prin oboseala poate fi oprita prin stoparea sau blocarea cresterii fisurii, aspect determinat de limitarea avansarii fisurii. Acestea reprezinta pozitii succesive ale frontului fisurii care se propaga prin deschideri sau inchideri succesive. Liniile de oprire se formeaza printr-o initiere si propagare a fisurii datorita ruperii ductile, transgranulara. La modificarea directiei de propagare se produc striuri intre liniile de oprire. Uneori se pot observa linii de oprire fragila intre fisuri, in cazul ruperii intergranulare.

Daca fisura este intergranulara si in acest caz striurile nu pot fi observate, respectiv in cazul ruperii determinata de temperaturi inalte sau daca exista o coroziune intergranulara.

Ruperea prin oboseala nu se produce brusc in toata sectiunea transversala a unei piese, intotdeauna fiind distinse trei faze:

v     initierea fisurii;

v     propagarea stabila a fisurii;

v       propagarea instabila a fisuriicare conduce la atingerea unei lungimi critice de fisura si determina ruperea prin oboseala a elementelor de rezistenta. Acest aspect poate fi pus in evidenta printr-o curba de tip sigmoida in care se reprezinta viteza de propagare a fisurii notata prin da/dN in raport cu factorul de intensitate a tensiunii notat pein DK.

3.2 Studiul oboselii prin analiza tensiunilor

In cele mai multe cazuri practice, solicitarile la oboseala sunt determinate de o stare de incarcare cu o variatie ciclica sau periodica a tensiunii, intre o valoare maxima s_max o valoare minima s_min a tensiunilor, valori care nu se modifica in timp si determina o variatie continua a tensiunii intre cele doua marimi. In functie de tensiunile extreme pot fi definite urmatoarele elemente ale unei solicitari ciclice, figura 3.2:

v     tensiunea medie s_m s_max s_min

v     amplitudinea solicitarii : s_v s_max s_min

v     variatia tensiunii: Ds s_max s_min

Fig. 3.2

In raport cu coeficientul de asimetrie R, celelalte elemente caracteristice ale unui ciclu de solicitare sunt redate prin relatiile (3.1):

(3.1)

a.

b.

c.

d.

Fig. 3.3

a)  solicitari oscilante (ondulatorii) cand tensiunile extreme sunt de acelasi semn:

v     oscilante pozitive, pentru 0 < R < 1, figura 3.3 a;

v     oscilante negative, pentru R >1;

b) solicitari pulsante (pulsatorii) cand una din tensiunile extreme este nula :

v     pulsante pozitive, pentru s_min s_m s_max s_v ; R = 0

v     pulsante negative, pentru s_max s_m s_min / 2; R ¥ figura 3.3 b;

c) solicitari alternante, cand s_max > 0; s_min < 0;

v     alternante asimetrice, pentru R < 0; R ¹ -1, figura 3.3 c;

v     alternante simetrice, pentru s_max s_min s_m = 0; R = -1, figura 3.3 d. Daca R = 1 avem o solicitare statica cu tensiune constanta.

Existenta unui defect sau modificarea sectiunii transversale determina un concentrator de tensiune care implica o crestere a tensiunii, conducand la aparitia unei stari de deformare elasto-plastica normala. Daca o epruveta sau o piesa este solicitata ciclic cu o amplitudine suficient de mare, se poate initia si apoi extinde o fisura sau un defect care conduce in final la ruperea dupa un anumit numar de cicluri de solicitare numit durabilitate. Pusa in evidenta intr-un sistem de axe, tensiunea in raport cu durabilitatea determina o curba (N) numita curba de durabilitate a materialului sau curba lui Wöhler, sau curba N.

Reprezentarea acesteia poate fi facuta in mai multe moduri :

v     reprezentare la scara normala, figura 3.4 a;

v     reprezentare la scara semilogaritmica, figura 3.4 b;

v     reprezentare la scara logaritmica, figura 3.5.

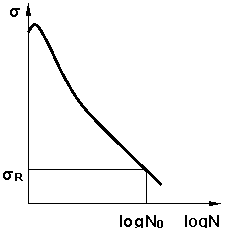
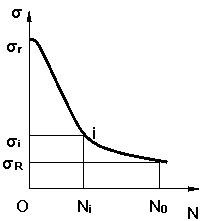
a.                                                 b.

Rezistenta la oboseala este valoarea cea mai mare a tensiunii pentru care oricat de mare ar fi numarul de cicluri de solicitare, piesa nu se rupe prin oboseala. Curba de durabilitate tinde asimptotic la valoarea respectiva.

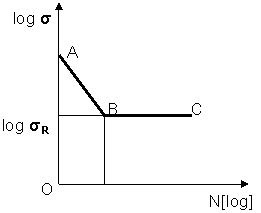
Fig. 3.5

Rezistenta la oboseala se noteaza cu _R unde R este coeficientul de asimetrie. Pentru materiale ductile, de tipul aluminiului, rezistenta la oboseala se determina arbitrar ducand o verticala la un numar de cicluri N_B, numit baza de incercare, care poate fi 10⁷ 10⁸ cicluri. Punctul in care intersecteaza curba determina limita de oboseala arbitrara si care se noteaza cu _N

Principalele tipuri de solicitari implica urmatoarele notatii pentru rezistenta la oboseala :

v       reprezinta rezistenta la oboseala pentru o solicitare alternant simetrica de incovoiere;

v       reprezinta rezistenta la oboseala pentru o solicitare pulsant pozitiva de incovoiere;

v       _-1t reprezinta rezistenta la oboseala pentru o solicitare alternant simetrica de tractiune - compresiune;

v       t reprezinta rezistenta la oboseala pentru o solicitare de rasucire alternant simetrica;

v       t reprezinta rezistenta la oboseala pentru o solicitare de rasucire pulsanta.

3.3 Factorii care influenteaza ruperea prin oboseala

Rezistenta la oboseala a materialelor este o marime conventionala care este stabilita pentru un anumit material si se determina pentru epruvete standardizate, cu un anumit diametru, cu suprafata exterioara lustruita si care lucreaza intr-un mediu fara agenti nocivi. Pentru anumite piese reale solicitate la oboseala, avand forme diferite, rezistenta la oboseala a materialului va varia fata de cea obtinuta pe epruveta. In calculul de rezistenta la solicitarile variabile, se urmareste sa se determine un coeficient de siguranta al elementului solicitat fata de rezistenta la oboseala a epruvetei standardizate.

Factorii principali care influenteaza rezistenta la oboseala se impart in trei grupe:

a)     factori constructivi: - forma piesei;

- dimensiunile piesei;

b)     factori tehnologici:    - calitatea materialului;

- rugozitatea suprafetei;

- tratamente termice de suprafata;

- ecruisarea materialului;

- tensiunile remanente.

c)     conditiile de lucru: - felul solicitarii;

- tipul ciclului de solicitare;

- suprasolicitari;

- subsolicitari;

- solicitari dinamice;

- agenti corozivi;

- temperatura de lucru;

- frecventa solicitarii.

Factori constructivi

Influenta concentrarii tensiunilor

Cauzele de natura constructiva ca discontinuitatile geometrice provenite din variatia brusca a dimensiunii piesei, gauri, crestaturi, asamblare cu strangere, care au ca efect o marire locala a tensiunilor se numesc concentratori de tensiune. Efectul concentratorilor de tensiune asupra rezistentei epruvetei standardizate se exprima cantitativ prin anumiti coeficienti. Fenomenul de concentrare a tensiunilor se manifesta diferit la solicitarile statice, variabile sau socuri, astfel marimea coeficientilor va depinde de felul solicitarii, respectiv geometria concentratorului.

v     Solicitari statice

In cazul solicitarilor statice se defineste ca factor teoretic de concentrare a tensiunii K, sau a_K, raportul dintre valoarea tensiunii maxime reale, calculate pentru elementul respectiv folosind elementele teoriei elasticitatii sau determinate experimental, s_max,real si tensiunea nominala s_n calculata pe baza relatiilor din Rezistenta materialelor, pentru solicitari statice, relatiile (3.2):

(3.2)

unde : s_max,real t_max,real, reprezinta tensiunea maxima produsa in sectiunea cu discontinuitati, salturi de diametre, solicitata static.

Pentru solicitarile simple, tensiunea nominala se calculeaza cu relatiile (3.3):

- pentru solicitari axiale;

- pentru solicitari de incovoiere; (3.3)

- pentru solicitari de rasucire.

Marimile A, W_y, W_p reprezinta aria, modulul de rezistenta axial, respectiv modulul de rezistenta polar al sectiunii transversale, pentru zona cu discontinuitati a piesei, (pentru sectiunea minima). Tensiunile care apar sunt maxime in vecinatatea concentratorului de tensiune, figura 3.6.

Cazul (a) reprezinta variatia tensiunii pe sectiunea transversala a unei platbande cu un concentrator de tipul unei gauri centrale, tensiunea maxima apare in vecinatatea acesteia, figura 3.6 a. Cazul (b) reprezinta starea complexa de tensiune pentru un arbore cu un canal radial, aceasta fiind determinata de tensiunea normala s orientata dupa directia longitudinala (directia de solicitare), tensiunea normala s orientata dupa directia circumferentiala si tensiunea s dispusa dupa directia radiala, figura 3.6 b. In vecinatatea defectului tensiunea maxima care poate produce ruperea piesei este s intre tensiuni existand corelatia:

(3.4)

v     Solicitari variabile

In cazul solicitarii variabile, concentratorul de tensiune scade foarte mult rezistenta la oboseala, influenta acestuia fiind concretizata prin coeficientul efectiv de concentrare a tensiunilor notat prin K_s, sau b_K , sau K_f si reprezinta raportul dintre rezistenta la oboseala a unei piese etalon fara concentrator s_R si rezistenta la oboseala a unei piese cu concentrator s_R,K , relatiile (3.5):

respectiv (3.5)

unde: s_R t_R reprezinta rezistenta la oboseala a unei piese de aceleasi dimensiuni, lustruita si fara concentrator, iar s_R,K t_R,K reprezinta rezistenta la oboseala a unei piese reale cu concentrator.

Fig. 3.6

Acest coeficient depinde de forma geometrica a concentratorului, de materialul piesei si se poate determina experimental. Se observa diferenta dintre coeficientul K_t , definit prin raportul a doua tensiuni, si coeficientul K_s , definit ca raport a doua rezistente la oboseala.

Elementul care exprima cel mai bine comportarea materialului la solicitari variabile periodice, in cazul prezentei unui concentrator, fata de efectul teoretic de concentrare a tensiunilor K_t , este coeficientul de sensibilitate h_K definit prin relatia (3.6):

respectiv (3.6)

Coeficientul de sensibilitate nu este constanta de material, el variind in functie de tipul defectului, de dimensiunile epruvetei si de tipul incarcarii.

Influenta dimensiunii piesei

Diagrame ale rezistentelor la oboseala

3.5. Calculul coeficientului de siguranta la oboseala la durabilitate nelimitata

3.6 Calculul coeficientului de siguranta la solicitari variabile compuse

O solicitare variabila compusa implica aplicarea simultana a doua sau trei tensiuni variabile, s sI t pentru starea plana de solicitare, respectiv s s sI s pentru starea spatiala de solicitare. Acestea conduc la introducerea unor teorii de rezistenta pentru determinarea unei tensiuni echivalente, care se compara cu starea limita de la solicitarea uniaxiala.

R s_{-1 p} t_max,L t_vL s_max,L s_vL iar ecuatia elipsei devine:

Expresia este valabila pentru orice valoare a amplitudinilor s_vL sI t_vL

Daca s_vL Þ

Pentru solicitari alternant simetrice de rasucire:

t_max t_vL t_{-1 p} s_vL Þ

relatie care introdusa in expresia ecuatiei elipsei rezulta:

Curba BLA reprezinta un sfert de elipsa cu coeficient de siguranta c = 1, iar sfertul de elipsa omotetic B¢LA₁,reprezinta locul geometric al punctelor cu coeficient de siguranta c la solicitarea variabila compusa, figura 3.23.

Punctului M( s_v t_v ii corespunde ciclul limita L( s_vL t_vL

Se cunoaste ca :

de unde:

, iar c este coeficientul de siguranta la solicitarea compusa. Considerand solicitarile simple (s si t pentru piesa:

(3.52)

Relatiile sunt particularizate pentru ciclurile de solicitari variabile simple, alternant simetrice, de incovoiere si de rasucire. Inlocuite in expresia elipsei, aceasta devine:

(3.53)

Relatia este folosita pentru calculul coeficientului de siguranta global la solicitarea variabila in functie de coeficientii de siguranta partiali, c_s sI c_t . Acestia se pot calcula cu relatiile determinate in paragrafele anterioare in functie de particularitatile piesei reale :

(3.54)

Pentru materiale fragile Gough sI Pollard, au propus curba ciclurilor limita tot o elipsa, deplasata , exprimata prin relatia:

Pentru materialele tenace : s_cr s_c s

In acest caz : F = 2, iar relatia (3.56) se reduce la relatia (3.53)