Radiocomunicatii

Radiocomunicatii

Oscilatoare

Cuprins

1. Analiza circuitului oscilator Hartley

2. Analiza circuitului oscilator Colpttis

3. Analiza circuitului oscilator Clapp

4. Analiza circuitului oscilator acordat la intrare si iesire

5. Oscilatoare neacordate

6. Stabilitatea oscilatorului si puritatea spectrala

7. Cristale di oscilatoare cu cristal

8. Oscilator cu cristal Pierce

Introducere

2-1. Oscilatorul Hartley - analiza circuitului

1. Verificarea reactiei pozitive. Presupunem ca tensiunea emitorului devine pozitiva datorita unei oscilatii sau zgomotului. Q₁ va tinde spre taiere iar tensiunea pe colector creste spre V_cc. Aceasta tensiune crescatoare este divizata in raportul n₂/(n₁+n₂), dar va avea aceeasi faza ca si in colector cu exceptia unei mici cantitati datorate incarcarii pe rezistenta de sarcina R_L. Semnalul reintors -reactia- la emitor prin C₁ va fi in faza cu semnalul initial f_osc. Determinarea incarcarii suplimentare datorita sarcinii: sarcina de 50Ω atunci cand este reflectata spre colector are un efect de sarcina R'_L, unde R'_L = R_L()²_, R'_L = 50()² = 24,2 kohmi

Incarcarea datorata lui Q_u finit al bobinei primare este calculata astfel - la 1MHz X_L=333Ω si R_bob=Q_uX_L = 50*333=16,7 KΩ

Privind de la priza n₁-n₂ la stanga se vede ca re||RE=(26mV/Ic)||1Kohm~25 ohmi. Prin urmare asa cum s-ar vedea privind de sus circuitul rezonant

R'_e = ()² (re||RE) (eq 2.5)

R'_e =(110/5)² Ω = 3KΩ (eq 2.5)

Asadar incarcarea totala a colectorului este :

R'_c = r_c||R'_L||R'_e

R'_c=50K||24,2K||16,7||3K=2,2K sau

G=0.002+0.041+0.06+0.32=0,45 mS, astfel R=1/G =2,2KΩ

Amplificarea in bucla la rezonanta pentru amplificator in conexiunea baza comuna

A_v=R'_c/r_e

A_v=2,2K/26=84,6 (=38.5 dB)

Pentru a afla daca circuitul oscilator are castig suficient se calculeaza amplificarea pe bucla si apoi se verifica daca este mai mare ca unitatea.

Bp= condensator de trecere (X_C = 0)

Se dau

n₁ = 100 spire, n₂ = 10 spire, n₀ = 5 spire

r_c = 50kΩ, incluzand efectele datorate unui emitator nedecuplat

L_p = 53μH; Q_u=50

C_CB = 1pF

C1 acordeaza circuitul pe 1MHz.

Daca desfacem circuitul asa cum se arata in fig 2-4 pentru a avea o idee cum va arata tensiunea de reactie v_fb pentru un v_i dat trebuie sa includem efectele de sarcina incarcarea, re||1K care ii va apartine cand bucla este inchisa si functioneaza. Amplificarea A_v poate fi foarte diferita in prezenta si in lipsa efectelor de incarcare cu impedanta de sarcina.

A_v = 84,6 cum s-a calculat anterior dar daca se ignora incarcarea data de re||1k , amplificarea ar parea sa fie A_v=(50k||24,2k||15K)/26 ohmi = 7,8K/26=300, ceea ce este cu 11 dB mai mare decat realitatea atunci cand se inchide bucla. O eraoare ca acestea poate avea ca rezultat un odcilator care nu functioneaza. Daca v_i=100mV, atunci o sa avem v_c = A_vv_i = 8,46 mV(nu exista inversie de faza la conexiunea baza comuna). Asadar v_fb= v_c

v_fb = (10/110) 8460 mV = 769 mV

mult mai mare decat intrarea de 100 mV. Se obtine astfel o amplificare pe bucla de A_vB = 84,6*(10/110). Deoarece 7,69 >>1, exista suficient castig pe bucla pentru a asigura oscilatiile intretinute pentru a avea o idee despre utilizarea condensatorului variabil , trebuie sa luam in considerare capacitatea deja existenta intre colector si masa. Orice capacitate asociata cu R_L se reflecta in circuitul colectorului ca C/(N²), unde N=110/5 . De asemenea , daca privim spre stanga dinspre punctul de priza (ramificatie), vedem C_BE la masa. In orice caz , aceste capacitati sunt mici iar efectul lor la colector este chiar mai mic intrucat ele se reflecta C/(N²).

Sa privim la C_CB dinspre colector la masa. Ar fi tentant sa aplicam efectul Miller ce ar duce la cresterea acestei capacitati, dar in acest caz nu ar fi corect, deoarece noi am luat in considerare un amplificator baza comuna. Nu actionam asupra bazei comune(baza e legata la masa), ci asupra emitorului. Asadar curentul alternativ care trebuie furnizat emitorului nu este afectat de C_CB. C_CB =1pF este vazut doar de la colector spre masa - peste circuitul rezonant. Cand se adauga la capacitatea fixa de 430 pF, circuitul rezonant paralel prezinta 431 pF catre masa.

Pentru a acorda 53 μH pe 1MHz se cere:

C = 1/(2f)²L

C = 1/[(210⁶)()]

Astfel, in cazul nostru, condensatorul variabil trebuie acordat la aproximativ 47 pF. Poate fi utilizat un trimer de 100 pF(max). Condensatorul variabil va compensa usor capacitatile parazite care sunt imposibil de prevazut exact.

2-2. Oscilatorul Colpitts

Oscilatorul Colpitts seamana cu oscilatorul Hartley, dar semnalul de reactie este luat de pe un divizor de tensiune capacitiv. Reactia este de data aceasta sopre emitorul tranzistorului Q₁, ci nu spre baza Q₁.Verificarea faptului daca faza este potrivita pentru a permite oscilatiile se face intrerupand bucla in locul marcat cu 'x', langa emitor si urmarind faza de-a lungul buclei. Rezultatul va fi acelasi ca si la oscilatorul Hartley.

Un lucru remarcabil este inductanta variabila, folosita pentru acord. Ea este de fapt un transformator cu miez de fier, reglabil cu mare permeabilitate. Analizand amplificarea pe bucla pentru oscilatorul Colpitts se tine cont de faptul ca atunci cand

rezistenta catre masa, peste C₁ este cel putin cu un ordin de marime mai mare decat X_C , atunci factorul de reactie este:

B=v_e/v_c = C₂/(C₁+C₂) = C_eq/C₁     (2-9a)

cu C_eq =C₁C₂ /(C₁+C₂) (2-9b)

De asemenea, incarcarea rezistiva in paralel pe circuitul rezonant este o combinatie intre R'_L si R'_e unde R'_L = (n_p/n_s)²R_L (2-10)

Figura 2-5 a) Oscilatorul Colpitts cu inductor variabil pentru acord

b) Circutul echivalent

iar R'_e=(C₁/C_eq)²(re||RE) (1/B)²r_e (2-11)

Oscilatorul Clapp

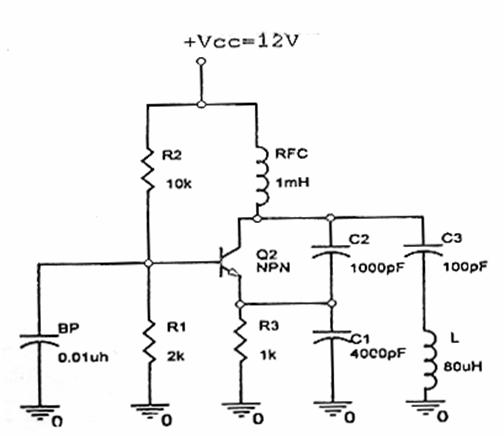
Oscilatorul Clapp fig 2-8 seamana cu Colpitts, dar in serie cu bobina L apare un mic condensator C₃. Capacitatea lui este mai mica decat cea a lui C₁ sau C₂, asfel incat reactanta lui este mai mare si astfel va avea cel mai important rol in determinarea frecventei de rezonanta.

C_eff=^-1.

In aceasta schema C₁ si C₂ pot fi schimbati pentru a obtine reactia dorita iar C₃ poate fi un condensator variabil pentru stabilirea frecventei de oscilatie. De asemnea C₃ ar putea avea un coeficient de temperatura negativ pentru a imbunatatii stabilitatea frecventei oscilatorului

Oscilatorul acordat la intrare si iesire

Oscilatoare neacordate

Oscilatorul cu punte Wien

Multivibrator astabil

Multivibrator astabil cu AO

Circuitul integrat prezentat in Figura 2-13 este un comparator de tensiune, astfel incat atat timp cat v₃ este mai mare decat v₂, iesirea este in mod ideal 0 constant v₀ = +v_cc. Daca v₃<v₂ iesirea are valoarea v₀ = -v_e. R₁ si R₂ impart v_o in raportul R₁/(R₁+R₂) astfel incat v₃= v_oR₁/(R₁+R₂)

Din figura 2-13, v₃ este fie +6V fie -6V. In acelasi timp C se incarca de la valoarea punctului anterior de comutare a lui v₃ spre v₀ prin rezistorul R. Figura 2-14 arata forma de unda a tensiunii de intrare si iesire din circuitul integrat. La momentul t₀ iesirea tocmai a comutat la aproximativ V_cc =12 V divizarea prin R₁ - R₂ va duce v₃ la 6V. v₂=-6V la t₀ este tensiunea pe C. Aceasta nu se poate schimba brusc, astfel ca la t₀ + caderea pe R este v₀-v₃ = +12 -(-6)=18V, iar curentul de incarcare al condensatorului este I_c(t₀+) = IR = =18V/47K =0,38 mA

Tensiunea pe C, v₂, creste exponential spre 12 V cu o canstanta de timp RC =47Ω0,001μF = 0,47ms. v₂ nu atinge niciodata 12V pentru ca la t1, cand v2 depaseste +6 V, circuitul integrat comuta in cealalta stare stabila. Timpul necesar

ca tensiunea pe piniul 2 creasca de la -6V la +6V se obtine din v2=vc=-6+(18)(1-e la -t/RC). Rezolvand pentru t, cu v2=+6V, rezulta ca 12/18=1-ela-t/RC,

iar ela -t/RC = 1-2/3 = 1/3. De aici -t/RC =ln (1/3) -1,1; iar t=1,1 RC =0,517 ms. t este o jumatate de perioada a undei dreptunghiulare de iesire, deci f₀ = 1/T = 1/2t = =1/(2,2RC) =267 Hz. Asadar v₀ =±V_cc cand |V_EE|=V_CC

v₃=±v₀R₁/(R₁+R₂)

t=-RCln (R₂/(2R₁+R₂))

fo=1/(-RCln (R₂/(2R₁+R₂)))

2.6 Stabilittatea oscilatorului si puritatea spectrala

Oscilatoarele sunt circuite relativ simple, dar performantele lor sunt critice

pentru sistemele de comunicatii. Printre parametrii oscilatoarelor care influenteaza

caracteristicile emitatoarelor si receptoarelor sunt: stabilitatea frecventei -incluzand variatiile zgomotului de scurta durata si deriva pe termen lung- si puritatea semnalului-incluzand si variatiile amplitudiniii semnalului determinate de zgomot si continutul in distorsiuni armonice.

Puritatea spectrala a semnalului poate fi controlata cu filtre si circuite dde control automat al castigului AGC. AGC poate de asemenea imbunatatii

variatiile zgomotului de scurta durata, dar se impune ecranarea circuitului

si filtrarea liniilor de alimentare pentru a minimiza zgomotul.

Parametrul de performanta critic al unui oscilator este deriva frecventei

Stabilitatea frecventei -pe termen lung - este afectata de imbatranirea componentelor care controleaza oscilatorul. de asemenea variatiile cu temperatura afecteaza comp[onentele care controleaza frecventa favorizand deriva

Aceste ultime modificari ale frecventei sunt caracterizate de catre

coeficientii de temperatura ai componentelor si de modul cum acestia influenteaza

stabilitatea cu temperatura a oscilatorului. Coeficientul de temperatura TC al unui parametru de sistem este

fractiunea cu care s-a modificat acesta per grad: TC= f₀/f₀

Fractiunea care reprezinta modificarea parametrului se da - de obicei - in procente sau in parti per milion (ppm), iar variatia temperaturii in grade ºC. De exemplu TC al frecventei unui oscilator poate fi +100ppm /ºC.

Aceasta inseamna TC= f₀/f₀= +100Hz/MHz per ºC. Daca temperatura creste

cu 20 ºC - atunci oscilatorul pe 5 MHz va prezenta o crestere de frecventa :

f₀/f₀ = TC T f₀=TCxTxf₀

f₀/f₀ = (+100Hz/MHz/0C)x200C f₀=+2kHz/MHz x 5MHz

f₀/f₀ = +2kHz/MHz f₀= +10 kHz

Asadar frecventa creste cu 10 kHz cand temperatura creste cu 20 ºC.

Stabilitatea cu temperatura a oscilatoarelor

Frecventa unui oscilator variaza cand temperatura circuitului variaza, datorita componentelor care controleaza frecventa ai caror coeficienti de temperatura sunt diferiti de 0. Principalii vinovati sunt condensatorii tipic construiti in sistem sandwich, un material dielectric intre doi conductori (armaturile). Capacitatea este data de :

C = ε A/d

unde A este suprafata armaturilor, d este distantra dintre ele, ε = constanta dielectrica a materialului dintre armaturi.