Reducerea sistemelor particulare de forte
In afara sistemelor de forte concurente, a caror reducere a fost studiata separat in cap.3.2, prezinta o importanta deosebita fortele coplanare si fortele paralele.
1 Reducerea fortelor coplanare
|
Fig.3.30 |
Pornind de la forma generala a torsorului de reducere al unui sistem de forte oarecare in raport cu un punct O, respectiv:
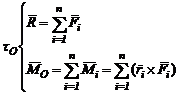(3.55)
se considera pentru simplificare ca toate
fortele sistemului sunt coplanare in xOy
(fig.3.30). In acest caz, pentru o forta oarecare 
a sistemului
(3.56)
Proiectiile pe axe ale rezultantei vor fi:
(3.57)
Momentul fortei fata de
punctul O este:
(3.58)
Observand ca 
, proiectiile pe axe ale momentului rezultant sunt:
(3.59)
Sintetizand, torsorul de reducere al fortelor coplanare va fi:
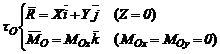(3.60)
Rezultanta sistemului este si ea coplanara cu fortele ce il compun, in timp ce momentul rezultant este perpendicular pe planul acestora. Efectul sistemului va consta dintr-o tendinta de translatare in plan a corpului, simultana cu o rotatie in jurul unei axe perpendiculare pe plan.
Referitor la invariantii sistemului se observa ca
(3.61)
In consecinta, sistemul de forte coplanare nu va putea fi echivalat cu un torsor minimal. Facand inlocuirile corespunzatoare in ecuatia (3.54) a axei centrale, respectiv
(3.60)
se obtine
(3.61)
Aceste relatii demonstreaza ca axa centrala este si ea coplanara cu fortele sistemului.
Referitor la cazurile de reducere analizate in cap.5, echivalenta valabila in cazul fortelor coplanare este:
Cazul 1 : 
– echilibru;
Cazul 2 : 
– cuplu de forte
actionand in planul sistemului sau paralel cu acesta;
Cazul 3 : 
– forta unica,
egala cu rezultanta, actionand in punctul O;
Cazul 4 : 
– forta unica,
egala cu rezultanta, actionand pe axa centrala.
|
