12.1 Introducere
Metodele de conducere conventionala se bazeaza pe o modelare corespunzatoare a sistemului supus reglarii si o tratare analitica cu ajutorul functiilor de transfer sau a ecuatiilor de stare. În majoritatea cazurilor, o tratare completa a problemei conducerii impune cunostinte avansate de matematica si sisteme de conducere.
În contrast cu tehnicile conventionale, metodele fuzzy de conducere ofera solutii mult mai pragmatice, cu evidente facilitati de aplicare în domenii diverse, impunând cunostinte de nivel acceptabil în domeniul sistemelor, logica de control si tehnologie.
Utilizarea logicii fuzzy în implementarea unor sisteme de conducere în conditiile absentei unei informatii totale asupra sistemului a reprezentat, de asemenea, unul din factorii care au determinat larga raspândire a controlului fuzzy în cele mai diverse domenii. Am asistat ( în ultimele doua decenii) si asistam la o adevarata explozie a tehnicilor de implementare de tip fuzzy atât în problemele clasice de control cât si în domeniul sistemelor expert, ale inteligentei artificiale sau în complexele probleme de decizii în domeniul economic.
Conceptul de Logica Fuzzy a fost introdus pentru prima data de Lotfi A. Zadeh de la Universitatea din California, Berkley, în 1965 în lucrarea Fuzzy Sets [1]. La acea epoca, de afirmare a calculatoarelor numerice bazate pe logica exacta 0, 1, un astfel de concept parea neverosimil. Zadeh, prin aceasta logica fuzzy a impus o alta modalitate de tratare a problemelor în care marimile ce determina evolutia unui sistem nu au frontierele clar definite, 0 sau 1, alb sau negru, aceasta putând fi asociate unei anumite zone incerte, "gri". De fapt, logica fuzzy da o noua interpretare a "logicii cu mai multe valori" formulata de Lukasievici [2]. De exemplu, sistemele ternare (cu trei valori logice 0, 1/2, 1) au fost studiate în nenumarate lucrari de algebra de comutatie, dar Zadeh a introdus conceptul de multime fuzzy, "vaga" pentru cazurile când frontiera valorii 1/2 are o caracteristica incerta.
Primele aplicatii ale acestui nou concept au aparut în jurul anilor 1975 în domeniile economic si medicina. Ulterior, japonezii au introdus metodele fuzzy în sistemele de control cu aplicatii diverse în industrie sau în echipamente electrocasnice.
Sfârsitul secolului trecut marcheaza o crestere spectaculoasa a metodelor fuzzy datorata atât noilor domenii de aplicatie: robotica, inteligenta artificiala, industrie usoara, industria materiilor compozite, navigatie, economie, etc., cât si extinderii geografice a noilor utilizatori în SUA si Europa.
12.2 Principiul logicii fuzzy
Logica fuzzy poate fi interpretata ca un concept de implementare a logicii umane în problemele de tip ingineresc. În limbajul uman exista diferite tipuri de inceritudini numite frecvent "incertitudini lexicale" care identifica imprecizia în evaluarea unor concepte sau în stabilirea unor concluzii.
Sa consideram cuvinte ca "barbat înalt", "barbat tânar" sau "zi calda", ce nu exprima foarte clar atributul asociat. Un barbat poate fi înalt daca are 1,80 m, dar unul care are numai 1,79 m nu poate fi considerat imediat ca unul de "înaltime medie". De asemenea, atributul de înalt poate fi diferit interpretat de un copil, pentru care toti barbatii sunt înalti, si altfel de un adult.
În aceeasi maniera se poate interpreta "barbat tânar". Pentru un om de 60 de ani, toti cei care au 54 de ani pot intra în aceasta categorie, ceea ce evident ca nu corespunde unor alte criterii de apreciere. Acesta poate fi considerat "între doua vârste" sau "în vârsta", dar delimitarea nu poate fi în nici un caz exacta.
Aceste exemple sugereaza faptul ca o eventuala abordare a acestor incertitudini într-o tratare logica necesita introducerea unui model matematic.
Sa reconsideram, pentru exemplificare, modelul lingvistic "barbati înalti". Într-o tratare conventionala, conform teoriei multimilor, multimea "barbati înalti" va cuprinde toti barbatii cu înaltime peste 1,77 m (de exemplu). Deci se poate introduce o functie care sa poata identifica exact apartenenta sau neapartenenta unui element (barbat) la aceasta multime (figura 12.1).
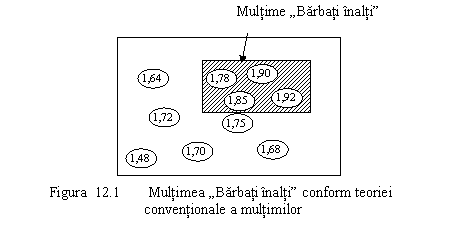
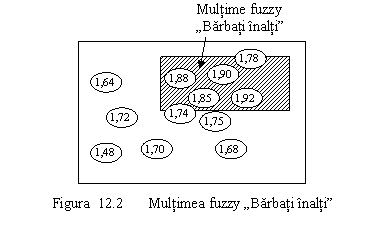
În figura 12.2 este
prezentata o multime în care elementele ei pot fi "mai mult sau mai
putin" definite ca "barbati înalti". Aceasta
multime este o "multime fuzzy".Fiecarui element al acestei
multimi i se poate asocia un anumit grad de apartenenta la
"barbati înalti". Acest grad este numit "grad al functiei
de apartenenta" m(x) al elementului x X.
Reprezentarea printr-o functie continua a functiei de apartenenta este redata în figura 12.3. Rangul lui m este de la 0 la 12.
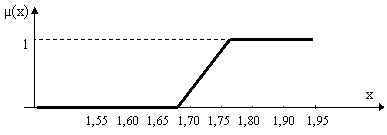
Figura 12.3 Functia de apartenenta m(x)

Figura 12.4 Functii de aprtenenta pentru câteva etichete lingvistice
Exemplul de mai sus poate fi extins si pentru alte "etichete lingvistice" cum ar fi: "barbati scunzi" si "barbati de înaltime medie" carora li se vor atribui functii de apartenenta corespunzatoare (figura 12.4).
Deci functia de apartenenta transforma X într-un spatiu M al functiei de apartenenta m(x). Daca M contine numai doua puncte 0 si 1, atunci caracterul incert dispare si se poate discuta de o multime conventionala (figura 12.5).
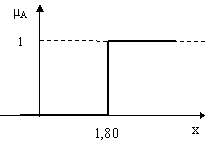
Figura 12.5
Daca se considera submultimea barbatilor cu înaltime "peste 1,80 m" atunci fiecare element x al universului de discurs poate apartine sau nu (cu certitudine) acestei submultimi:
mA:X
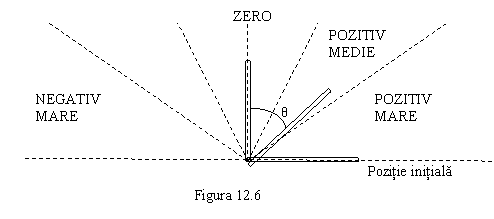
Sa
consideram universul X definit de multimea valorilor unghiulare ale
unui brat robot în coordonate cilindrice. În jurul pozitiei de
echilibru a bratului se pot defini urmatoarele etichete lingvistice:
ZERO, POZITIV MEDIE, POZITIV MARE, NEGATIV MEDIE, NEGATIV MARE, ceea ce
corespunde unei delimitari în coordonate unghiulare ca cea sugerata
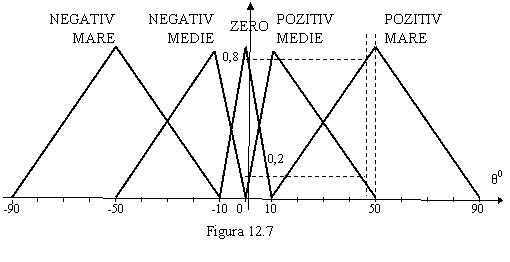
în figura 12.6. Acestora li se pot asocia functiile de
apartenenta reprezentate în figura 12.7.
Elementele prezentate mai sus permit introducerea conceptului de "multime fuzzy" si identificarea elementelor sale specifice.
O multime clasica (multime crisp) este definita ca o colectie de elemente sau obiecte x X care poate fi finita, numarabila sau nu. Daca consideram acum o submultime A, A X, un element x poate sa "apartina lui A" sau sa "nu apartina lui A". Daca x A atunci declaratia "apartine lui A" este adevarata, în caz contrar fiind falsa.
O
multime fuzzy ![]() este o multime de
perechi ordonate:
este o multime de
perechi ordonate:
![]()
unde ![]() este functia de
apartenenta a lui x în
este functia de
apartenenta a lui x în ![]() . De exemplu, sa consideram pozitia
bratului
. De exemplu, sa consideram pozitia
bratului ![]() . Pentru cele 5 variabile lingvistice reprezentate în Figura 12.7,
pozitia
. Pentru cele 5 variabile lingvistice reprezentate în Figura 12.7,
pozitia ![]() va fi definita
prin:
va fi definita
prin:
![]()
![]()
![]()
![]()
![]()
Deci, multimea fuzzy asociata multimii POZITIV MARE va fi:
![]()
Pentru submultimea ZERO obtinem:
![]()
În mod similar pot fi construite submultimile fuzzy pentru celelalte functii de apartenenta prezentate în figura 12.7.
O
notatie destul de frecvent întâlnita în literatura de specialitate
[2, 3] pentru un univers de discurs discret si finit este data de:
![]()
iar în cazul universului de discurs continuu si infinit se utilizeaza:
![]()
Functii de apartenenta
Exemplele precedente au pus în evidenta
importanta cunoasterii functiei de apartenenta în
conditiile definirii corecte a unei multimi fuzzy. Conform
elementelor prezentate anterior, considerând X un univers de discurs si o
submultime A a lui X, atunci submultimii fuzzy ![]() i se asociaza
functia caracteristica, functia de apartenenta:
i se asociaza
functia caracteristica, functia de apartenenta:
![]() (12.12)
(12.12)
prin care este specificat gradul prin care x este un membru al submultimii A.
Formele cele mai des întâlnite ale functiilor de apartenenta în aplicatii industriale sunt cele triunghiulare si trapezoidale (figura 12.8) [2], [3].

Figura 12.8 Functii de apartenenta triunghiulare si trapezoidale
Gradul de apartenenta este exprimat, în aceste cazuri, prin relatii liniare. În mod normal, aceste functii sunt definite prin punctele de referinta M1, M2, M3 sau M1, M2, M3, M4, respectiv.
Sunt utilizate de asemenea si alte forme [3] (figura 12.9).

Figura 12.9 Functii de apartenenta "clopot"
definite prin relatiile:
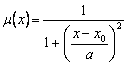 ;
; ![]()
respectiv:
![]() ;
; ![]()
unde x0 defineste pozitia vârfului pentru μ=1 iar a reprezinta largimea domeniului.
O functie de apartenenta care deriva din caracteristica trapezoidala si cea definita de relatia (12.14) poate fi determinata de relatiile [3]:
![]() ;
; ![]()
![]() ;
; ![]()
![]() ;
; ![]()
Forma acestei functii este prezentata în figura 12.10.
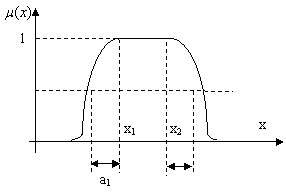
Figura 12.10 Functia de apartenenta definita prin relatiile (12.15 - 12.17)
Forma generala a unei functii de apartenenta este prezentata în Figura 12.112. În structura reprezentarii distingem urmatoarele zone:
baza
functiei de apartenenta definita ca acea regiune a
universului de discurs pentru care ![]() .
.
suportul
corespunde acelei regiuni a universului pentru care ![]() .
.
frontierele
functiei de apartenenta sunt definite ca acele regiuni pentru
care ![]() . Punctelor de pe frontiera le sunt asociate o
"anumita incertitudine".
. Punctelor de pe frontiera le sunt asociate o
"anumita incertitudine".
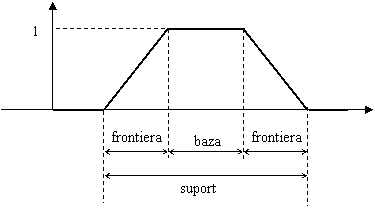
Figura 12.11 Forma generala a unei functii de apartenenta
12.4 Strategia de control lingvistica
Sa
reconsideram cazul comenzii unui brat de robot (figura 12.6). Sa
presupunem ca dorim sa miscam bratul din pozitia
initiala (![]() ) în pozitia de origine, dorita (
) în pozitia de origine, dorita (![]() ). Conducerea conventionala a bratului este
bazata pe procesarea erorii,
). Conducerea conventionala a bratului este
bazata pe procesarea erorii,
![]() (12.18)
(12.18)
utilizând regulatoare standarde PI sau PID (figura 12.12).

Figura 12.12 Sistem de conducere conventional
Algoritmul de control al bratului determina o lege de variatie a cuplului de actionare M(t) astfel încât eroarea stationara a sistemului sa tinda catre valoarea zero.
![]() (12.19)
(12.19)
O astfel de abordare impune o analiza exacta a miscarii bratului, determinarea ecuatiilor diferentiale ce guverneaza miscarea precum si calculul corespunzator al parametrilor regulatorului în scopul obtinerii performantelor dorite.
O tratare cu totul diferita de procedura de control conventionala este oferita de asa numita "strategie de control lingvistica". Un operator uman poate realiza un control cu performante acceptabile printr-o evaluare euristica a pozitiei (a erorii de urmarire) si luarea unor decizii corespunzatoare. În esenta, un operator va actiona dupa urmatoarele reguli:
Porneste bratul din pozitia initiala cu o valoare "medie" a cuplului M.
Daca distanta fata de pozitia dorita "mare", creste valoarea cuplului la o valoare "mare".
Daca distanta este "medie" el micsoreaza valoarea cuplului la o valoare "medie".
Daca distanta este "zero" valoare cuplului este redusa la "zero" sau se poate impune chiar o valoare "negativa zero" astfel încât sa fie realizata oprirea în pozitia dorita.
Regulile precizate impun introducerea unor multimi fuzzy corespunzatoare pe universul de discurs reprezentat de "cuplul de actionare". Conventional acestea vor fi notate prin: NEGATIV ZERO, POZITIV ZERO, MEDIE, MARE si carora li se va asocia functii de apartenenta de tip triunghiular (figura 12.13).

Figura 12.13 Functii de apartenenta ale cuplului de actionare
Scrise într-un formalism specific controlului fuzzy, regulile de mai sus sunt specificate prin asa numitele "reguli If-Then".
Regula 1 If Unghiul=POZITIV MARE
Then Cuplul=MARE
Regula 2 If Unghiul=POZITIV MEDIU
Then Cuplul=MEDIE
Regula 3 If Unghiul=ZERO
Then Cuplul=NEGATIV ZERO
Regulile prezentate mai sus definesc asa numitul mecanism de "inferenta" ce reprezinta o etapa importanta în introducerea conceptului "fuzzy" într-un sistem de conducere. Evident, aceste reguli au, în acest exemplu, o forma simpla, corespunzând problemei tratate.
Sa presupunem ca miscarea bratului din pozitia initiala pâna în pozitia dorita face parte dintr-un ciclu tehnologic de preluare a unei piese supusa unui proces de tratare termica. Introducând o noua variabila TEMPERATURA , asociindu-i acesteia domeniile: TEMPERATURĂ JOASĂ, TEMPERATURĂ MEDIE, TEMPERATURĂ MARE si asociindu-le functiile de apartenenta din figura 12.14, regulile prezentate mai sus vor introduce conditii suplimentare. Aceste conditii sunt impuse în corpului regulii prin operatori sI (AND), respectiv SAU (OR), în functie de logica interpretarii.
Astfel, noile reguli vor avea forma:
Regula 1 IF Unghiul=POZITIV MARE AND Temperatura =
TEMPERATURA JOASĂ
THEN Cuplul=POZITIV ZERO
Regula 2 IF Unghiul=POZITIV MEDIU AND Temperatura =
TEMPERATURĂ MEDIE
THEN Cuplul=MARE
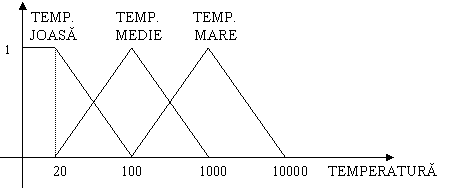
Figura 12.14 Functii de apartenenta ale variabilei Temperatura
Regula 1 se interpreteaza astfel: daca piesa ce urmeaza a fi preluata nu este suficient încalzita (TEMPERATURĂ JOASĂ) atunci miscarea bratului nu este necesara (Cuplu=POZITIV ZERO).
Pentru Regula 2 avem urmatoarea interpretare: daca Temperatura atinge valoarea necesara (domeniul TEMPERATURĂ MEDIE) si daca bratul are pozitia initiala (Unghiul=POZITIV MARE) atunci bratul este pus în miscare (Cuplu=MARE) pentru prinderea piesei, etc.
Desigur, în alte situatii pot apare si operatori de tipul SAU (OR) sau negatie (NOT) care implementeaza în concept fuzzy logica clasica.
12.5 Operatori în logica fuzzy
Operatorii uzuali NEGAŢIE, sI, SAU sunt tratati în logica fuzzy prin aplicarea regulilor "min", "max" asupra functiilor de apartenenta.
12.5.1 Operatorul SAU (OR)
Se vor considera trei multimi fuzzy ![]() ,
, ![]() ,
, ![]() , definite pe acelasi univers de discurs X. Operatorul
SAU corespunde operatiei de reuniune:
, definite pe acelasi univers de discurs X. Operatorul
SAU corespunde operatiei de reuniune:
![]() (12.20)
(12.20)
În tratarea fuzzy, operatorul este realizat prin functia de maxim aplicata la nivelul functiilor de apartenenta (figura 12.15):
![]()
În cazul în care variabilele sunt diferite, procedura se pastreaza:
![]()
Evident ca anumite proprietati ale algebrei logice conventionale (booleene), comutativitatea si idempotenta se pastreaza.
![]()
![]()
![]()
Operatorul SAU poate fi construit si prin operatia aritmetica de adunare, mai precis de mediere
![]() (12.25)
(12.25)

Divizarea prin 2 s-a impus pentru a exclude
eventualele depasiri a valorii 1 a functiilor rezultate prin
însumare.
Figura 12.15 Operatorul SAU realizat prin "maximum"
12.5.2 Operatorul sI (AND)
Ca si în algebra conventionala acest operator se obtine prin operatia de intersectie realizata la nivelul functiilor de apartenenta prin operatorul "minim":
![]()
![]() (12.27)
(12.27)
În figura 12.16 este prezentat operatorul sI prin operatia de "minim" aplicata functiilor de apartenenta.
Toate proprietatile descrise mai sus se regasesc si la acest operator:
![]()
![]()
![]()
![]()
În foarte multe aplicatii, operatorul sI este realizat prin operatia aritmetica de înmultire:

![]() (12.31)
(12.31)
Figura 12.16 Operator sI realizat prin operatia "minimum"
12.5.3 Operatorul NEGAŢIE (NOT)
Acest operator realizeaza complementul functiei de apartenenta în raport cu 1 (figura 12.17):
![]() (12.32)
(12.32)
![]() (12.33)
(12.33)
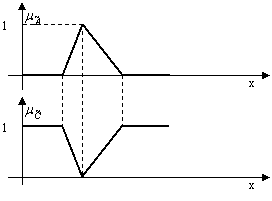
Figura
12.17 Operatorul NU (Negatie)
1.6 Proprietati generale ale unui sistem de conducere
în logica fuzzy
Sistemele conventionale de conducere ale unui robot (ale componentelor sale mecanice) se încadreaza în configuratia clasica a sistemelor de reglare (figura 12.18).

Figura 12.18 Sistem
conventional de conducere
Într-o astfel de structura, valoare dorita a variabilei de pozitie (de referinta) qd este comparata cu valoarea reala masurata de traductor (qT). Eroarea rezultata este procesata într-un regulator care genereaza marimea de comanda a sistemului de actionare u si prin aceasta este determinata miscarea elementului mecanic (bratul robotului):
![]()
Regulatoarele uzuale utilizate în aceste sisteme sunt de tipul P, PI si PID, ele asigurând, în conditii de alegere corespunzatoare a parametrilor regulatorului, performantele de control dorite.

Un sistem de conducere în
logica fuzzy (SCLF) respecta configuratia generala a
oricarui sistem de conducere, rolul regulatorului conventional fiind
preluat de un Controler în Logica Fuzzy (CLF) (figura 12.19).
Figura 12.19 Sistem de conducere în logica fuzzy
Un CLF va implementa, deci, un
algoritm de conducere care, prin procesarea erorii e (sau a unui vector eroare ![]() ) sa determine performantele calitative dorite
pentru întregul sistem de conducere, în mod curent obtinerea unei erori
stationare zero.
) sa determine performantele calitative dorite
pentru întregul sistem de conducere, în mod curent obtinerea unei erori
stationare zero.
În contrast cu regulatorul standard, CLF nu implementeaza o relatie mate-matica bine definita (algoritmul de reglare) ci utilizeaza inferente cu mai multe re-guli bazate pe variabile lingvistice si care sunt tratate prin operatori în logica fuzzy.
Configuratia generala a unui CLF cuprinde trei parti (figura 12.20) [2, 3, 6]:
Fuzificare
Inferente (baza de reguli)
Defuzificare.

Figura 12.20 Structura unui CLF
Blocul de fuzificare transforma datele de intrare, eroarea sistemului, în marimi fuzzy, atribuind acestor marimi variabile lingvistice si asociindu-le functii de apartenenta corespunzatoare.
Blocul de inferente reprezinta partea principala a unui CLF. Acest bloc genereaza legea de control sub forma unei familii de reguli logice de tipul IF...THEN ce descriu relatiile între intrarea e (eroare) si iesirea u a controlerului. Adaptând un model direct, aceste reguli implementeaza de fapt o lege de forma generala:
![]() (12.34)
(12.34)
Din considerente practice,
implementarea unei astfel de legi pentru ![]() este extrem de complexa si dificil de aplicat. În
mod curent, legea de control de mai sus capata forma
simplificata:
este extrem de complexa si dificil de aplicat. În
mod curent, legea de control de mai sus capata forma
simplificata:
![]() (12.35)
(12.35)
sau:
![]() (12.36)
(12.36)
Existenta unei legi de conducere de tipul (12.42)-(12.6.44) nu înseamna ca CLF poate fi definit printr-o functie de transfer sau printr-o ecuatie de diferente. Legea de control este generata prin baza de reguli IF...THEN sub forma:
![]() (12.37)
(12.37)
si deci iesirea actuala se obtine sub forma:
![]() (12.38)
(12.38)
un astfel de CLF este numit CLF-Mamdani dupa numele cercetatorilor Mamdani si Assilian care l-au propus prima data în anul 1975 (figura 12.21) [12].
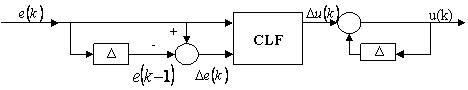
Figura 12.21 Variabilele de intrare si iesire într-un CLF
Fiecare din regulile bazei este caracterizata printr-o parte IF numita "antecedent" si o parte THEN numita "consecinta". Antecedentul unei reguli contine setul de conditii, consecinta contine concluzia. Modul în care opereaza CLF-ul este urmatorul: daca conditiile antecedentului sunt satisfacute, atunci concluzia, consecinta, este activa. Deci CLF-ul poate fi privit ca un sistem care are ca intrari variabilele incluse în antecedentele regulilor si ca iesire variabila inclusa în consecinta. Deci, se va putea defini eroarea e(k) si variatia ei Δe(k) ca intrari în sistem, iar iesirea poate fi reprezentata de variatia Δu(k) (figura 12.21). Un exemplu de regula poate fi urmatorul:
IF e(k) este POZITIV AND Δe(k) este ZERO
THEN Δu(k) este POZITIV
Este evident ca intrarile si iesirile unui CLF sunt stari, sau substari ale întregului sistem controlat, deci CLF poate fi privit si ca un controler de variabila de stare guvernat de o familie de reguli si un mecanism de inferenta fuzzy.
Ultimul bloc al unui CLF, blocul de defuzificare, asigura formarea unor semnale crisp, prin metode specifice, compatibile cu sistemele de actionare utilizate în controlul robotilor.
Elementele prezentate mai sus pot pune în evidenta caracteristicile generale ale sistemelor conduse prin metode bazate pe logica fuzzy si permit identificarea avantajelor si dezavantajelor acestor noi concepte de conducere.
Avantajele esentiale pot fi sumarizate în urmatoarele [10], [11, [12]:
nu se impune un model precis al sistemului condus;
strategia de conducere se bazeaza pe operatori lingvistici si o baza de reguli usor de implementat;
pot fi conduse procese complexe cu neliniaritati dificil de modelat;
implementarea se poate realiza tehnologic relativ facil fie prin proiectarea unor configuratii particulare de controlere, fie prin utilizarea unor procesoare dedicate.
Dezavantajele utilizarii acestor sisteme sunt:
nu exista o metodica precisa pentru realizarea tuturor fazelor implementarii unui CLF: fuzificare, inferente, defuzificare, în multe situatii solutiile adoptate având un caracter euristic, artizanal, nesistematic;
dificultatea demonstrarilor, în toate cazurile, a stabilitatii sistemelor;
posibilitatea aparitiei ciclurilor limita datorita functionarii pe caracteristici neliniare;
performantele sistemului condus pot sa nu fie întotdeauna la nivelul dorit;
imposibilitatea implementarii practice a unui CLF cu un numar mare de variabile de intrare (peste 4) datorita dimensiunii bazei de reguli implicata.
În orice caz, este evident ca sistemele de conducere în logica fuzzy reprezinta o alternativa clara fata de sistemele de conducere conventionale. Acest lucru este demonstrat de numeroasele aplicatii în economie si industrie, de volumul cercetarilor pe plan mondial în aceasta directie, de eforturile tehnologice pentru a pune la dispozitie resursele software si hardware specializate.
Fuzificarea marimilor în CLF
Dupa prezentarea generala a caracteristicilor de baza în SCLF, vom aborda în detaliu principalele aspecte ale procedurilor de implementare a unui CLF.
Interfatarea pe intrare a unui astfel de controler este realizata prin blocul de fuzificare. Acesta trebuie sa asigure:
Conversia marimilor de intrare (eroare) e într-o forma digitala compatibila cu procesarea ulterioara în logica fuzzy. Daca eroarea e este un semnal continuu, se impune o conversie analog-numerica corespunzatoare. De asemenea, daca e este un semnal numeric, o procesare numerica suplimentara este necesara pentru asigurarea performantelor dorite.
Formarea variabilelor ce vor determina conditiile antecedentului în baza de reguli a CLF. În general, asa cum s-a aratat anterior, o prima variabila de intrare este eroarea e(k), dar impunerea unor conditii complexe necesita generarea si a altor variabile de intrare. Acestea pot fi definite prin marimea de eroare evaluata la câteva momente de timp, e(k-1), e(k-2),..., e(k-v) sau de alte variabile de stare ale sistemului condus, cum ar fi viteza sau acceleratia bratului mecanic (pentru controlul unui sistem robot).
Exprimarea variabilelor de intrarea ca multimi fuzzy. În acest sens, marimilor fizice li se atribuie variabile lingvistice, variabile fuzzy si functii de apartenenta. Se determina totodata universul de discurs pe care este definita fiecare variabila.
Functiile de
apartenenta utilizate în sistemele de conducere au forme
triunghiulare sau trapezoidale. De asemenea, universul de discurs este frecvent
ales ca [-1,1] iar variabilele de intrare astfel definite sunt considerate
normalizate. Este evident ca aceasta impune utilizarea unor factori de
scala corespunzatori pentru fiecare variabila.
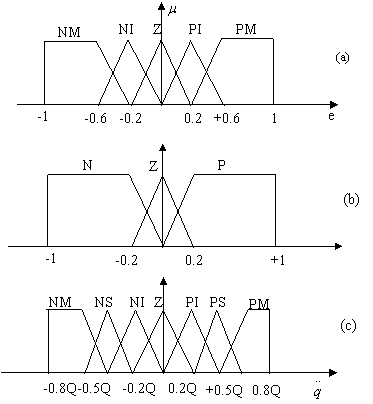
Figura 12.22 Functii de apartenenta ale variabilelor de intrare în CLF
În figura 12.22.a sunt reprezentate functiile de apartenenta a cinci multimi fuzzy ce reprezinta etichetele lingvistice ale erorii: NM, NI, Z, PI, PM (NEGATIV MARE, NEGATIV INFERIOR, ZERO, POZITIV INFERIOR, POZITIV MARE, respectiv). Rangul de operare al erorii, universul sau de discurs, se presupune [-1,1]. Se observa ca trei multimi au functii de apartenenta triunghiulare iar doua, trapezoidale.
În mod analog, în figura 12.22.b sunt reprezentate cele trei functii de apartenenta ale multimilor fuzzy asociate etichetelor lingvistice ale variatiei erorii Δe: N,Z,P (NEGATIV, ZERO, POZITIV) al carui univers de discurs este de asemenea normalizat.
În figura 12.22.c sunt prezentate
functiile de apartenenta ale multimilor fuzzy ce
reprezinta acceleratia miscarii (![]() ), în conditiile în care baza de reguli ce urmeaza
a fi stabilita impune introducerea acestor variabile. Sunt definite
sapte multimi fuzzy asociate etichetelor NM, NS, NI, Z,PI, PS, PM
(NS=NEGATIV SUPERIOR, PS=POZITIV SUPERIOR). Universul de discurs nu mai este
normalizat si este utilizat chiar domeniul de variatie al variabilei
de stare, acceleratia
), în conditiile în care baza de reguli ce urmeaza
a fi stabilita impune introducerea acestor variabile. Sunt definite
sapte multimi fuzzy asociate etichetelor NM, NS, NI, Z,PI, PS, PM
(NS=NEGATIV SUPERIOR, PS=POZITIV SUPERIOR). Universul de discurs nu mai este
normalizat si este utilizat chiar domeniul de variatie al variabilei
de stare, acceleratia ![]() .
.
Cele trei exemple prezentate mai sus ilustreaza faptul ca alegerea functiilor de apartenenta nu poate sa fie supusa unor reguli foarte precise. Acestea pot fi alese simetrice sau nesimetrice (în raport cu originea), triunghiulare sau trapezoidale, echidistante sau nu, pe universul de discurs normalizat sau nu. Totusi, indiferent de modalitatile de alegere se impun categoric respectarea urmatoarelor conditii:
![]() ,
, ![]()
![]() ,
, ![]()
Semnificatia
acestor conditii va fi ilustrata mai târziu dar o analiza
elementara indica ca relatia (12.39) impune ca pentru orice
punct din universul de discurs, U sa fie definita cel putin o
functie ![]() . A doua conditie este determinata de o
anumita comoditate în calculele numerice ale CLF.
. A doua conditie este determinata de o
anumita comoditate în calculele numerice ale CLF.
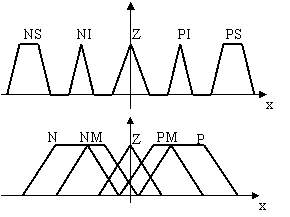
Figura 12.23 Forme ale functiilor de apartenenta
În figura 12.23 sunt prezentate câteva tipuri de functii de apartenenta care nu respecta conditiile (12.39), (12.40). Astfel de forme nu pot determina o implementare corecta a conceptului de logica fuzzy. Se remarca ca functiile descrise în figura 12.22 verifica cele doua conditii (12.39), (12.40), modelul lor servind ca referinta pentru implementari curente. Trebuie subliniat faptul ca, în functie de problema abordata, pot fi utilizate si alte tipuri de functii de apartenenta, cu forme specifice, particulare, [5, 6] care sa ofere anumite facilitati în generarea bazei de reguli (evident ca restrictiile (12.39), (12.40) trebuie sa fie satisfacute).
Pentru a evita eventualele confuzii ulterioare
mentionam ca particularitatile specificate mai sus
sunt valabile pentru functiile de apartenenta asociate numai
variabilelor de intrare într-un CLF. Variabilelor de iesire, marimile
crisp, li se asociaza de asemenea functii de apartenenta,
dar acestora nu li se mai impun restrictiv conditiile (12.39), (12.740).
Procesul de generare ale acestor variabile este defuzificarea si va fi
discutat ulterior. Functiile de apartenenta utilizate pot fi de
tipul celor prezentate în figura 12.22, dar pot avea si forma aparte ca în
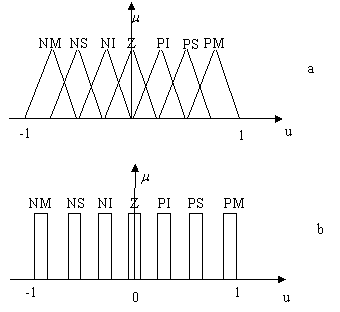
figura 12.24.b. Functiile de apartenenta din figura 12.24.a pot
intra în categoria "normale", acestea respectând conditiile (12.39), (12.40),
dar cele din figura 12.24.b, functii numite "singleton", nu verifica
nici una din conditii. Aceste functii sunt utilizate frecvent în
conditiile în care se doreste obtinerea, în procesul de
defuzificare, a unei relatii simplificate pentru variabilele de iesire.
Figura 12.24 Functii de apartenenta pentru variabilele de iesire
12.8 Baza de reguli
Partea principala a unui CLF, cea care implementeaza algoritmul de conducere al sistemului este baza de reguli (blocul de inferente) a sistemului.
Asa cum am aratat în paragrafele anterioare, fiecare regula este formata din doua parti: partea IF numita si antecedent si o parte THEN numita consecinta.
IF ![]()
THEN ![]()
IF ![]()
THEN ![]()
Antecedentul contine conditia sau conditiile (variabile de intrare) care activeaza regula. Daca mai multe variabile formeaza conditiile de activare, acestea sunt legate prin AND. Consecinta permite generarea variabilei sau a variabilelor de iesire activate ca urmare a îndeplinirii conditiilor regulii.

Pentru a fixa ideile vom
analiza baza de reguli pentru un sistem de conducere al unui brat în
miscare de translatie (figura 12.25).
Figura 12.25 Sistem de conducere al unui brat robot
Se va construi baza de reguli pentru un CLF cu doua variabile de intrare e(k) si Δe(k) si o variabila de iesire u(k). Se va presupune ca universul de discurs este normalizat atât în ceea ce priveste variabilele de intrare cât si pe cea de iesire, iar functiile de apartenenta au forma din figura 12.26.
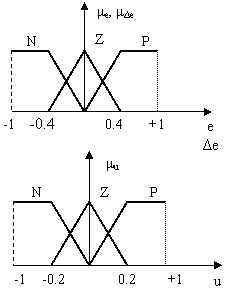
Figura 12.26 Functiile de apartenenta pentru e, Δe,u
Formarea corecta a bazei de reguli depinde de ordinul sistemului condus si de performantele dorite. În principiu, nu exista o procedura sistematica pentru determinarea regulilor, acestea fiind determinate în mare masura de abilitatea si experienta proiectantului. Totusi, pentru cazul analizat, regulile pot fi stabilite relativ usor, acestea fiind determinate de conditia evolutiei stabile a sistemului catre o dreapta de comutare [3], [7], [8]. Detaliile asupra acestei metode vor fi tratate ulterior.
În sinteza, baza de reguli pentru exemplul discutat, contine noua reguli în forma urmatoare:
Regula 1 IF e este N AND Δe este P
THEN u este Z
Aceasta regula sugereaza ca în conditiile în care eroarea este negativa si variatia ei este pozitiva, comanda generata u poate fi zero, evolutia sistemului ducând catre domeniul e=0. Celelalte reguli au interpretari similare.
Regula 2 IF e este Z AND Δe este P
THEN u este N
Regula 3 IF e este P AND Δe este P
THEN u este N
Regula 4 IF e este N AND Δe este Z
THEN u este P
Regula 5 IF e este Z AND Δe este Z
THEN u este Z
Regula 6 IF e este P AND Δe este Z
THEN u este N
Regula 7 IF e este N AND Δe este N
THEN u este P
Regula 8 IF e este Z AND Δe este N
THEN u este P
Regula 9 IF e este P AND Δe este N
THEN u este Z
Se remarca ca fiecare regula este definita prin operatorul logic AND (sI) ce defineste intersectia conditiilor logice asociate regulii. Desi, neformulat explicit, baza de reguli contine si operatorul OR (SAU) aplicat ca operator reuniune intrinsec pe multimea regulilor bazei. Exemplu anterior poate fi rescris sub forma urmatoare:
Regula 1 .......... ..... ...... ............. , OR
Regula 2 .......... ..... ...... ............. , OR
Regula 9 .......... ..... ...... ............. .
Descrierea de mai sus a bazei de reguli este asa numita "descriere lingvistica". Ea este utilizata frecvent în conditiile în care dimensiunea bazei este rezonabila, numarul de variabile de intrare în CLF nedepasind valoare trei. În mod frecvent, baza de date poate fi reprezentata sub forma tabelara si printr-o matrice de inferenta. De exemplu, regulile stabilite mai sus pot fi redate sintetic ca în Tabelul 12.12.
|
e |
N |
Z |
P |
|
P |
Z |
N |
N |
|
Z |
P |
Z |
N |
|
N |
P |
P |
Z |
Tabelul 12.1 Baza de reguli pentru variabilele e, ![]()
Matrice cuprinde, pe li 353c29d nii si coloane etichetele lingvistice ale variabilelor e si Δe, respectiv. Fiecare pereche linie, coloana defineste conditiile unei anumite reguli iar în celula corespunzatoare a matricei este introdusa eticheta lingvistica a valorii generate, u (consecinta).
Matricile de inferente de tipul celei prezentate sunt practice pentru baze de reguli cu un numar mare de variabile de intrare în CLF. De exemplu, daca conditiile în CLF sunt date de e, Δe si Δ2e (acceleratia sistemului), atunci baza de reguli poate fi sintetizata prin matricea de inferente din Tabelul 12.2.
|
|
N |
Z |
P |
||||||
|
N |
Z |
P |
N |
Z |
P |
N |
Z |
P |
|
|
P |
Z |
Z |
N |
Z |
N |
N |
Z |
N |
N |
|
Z |
P |
Z |
Z |
P |
Z |
N |
Z |
Z |
N |
|
N |
P |
P |
Z |
P |
P |
Z |
P |
Z |
Z |
Tabelul 12.2 Baza
de reguli pentru variabilele e,![]()
Procedura poate fi extinsa pentru structuri mai complexe, cu un numar mai mare de variabile de intrare, dar trebuie avut în vedere ca o crestere a complexitatii bazei de date implica o procesare mai laborioasa, prelucrarea unui numar mare de variabile, un timp de calcul sporit si multe inconveniente în implementarea practica a algoritmului de control.
12.9 Implementarea bazei de reguli
Este evident ca procesarea unor reguli într-o baza (mecanismul de inferenta) impune determinarea, în primul rând, a conditiilor ce definesc regula si a gradului lor de activare. Acest lucru este obtinut prin tratarea conditiei ca multime fuzzy si prin testarea gradului de activare al acesteia cu ajutorul functiilor de apartenenta asociate.
Într-o scriere sintetica, o regula poate fi exprimata sub forma:
Regula j: IF CONDIŢIA C1 AND CONDIŢIA C2 AND ... AND CONDIŢIA CP
THEN DECIZIA Dj
Considerând ![]() , multimea fuzzy asociata conditiei C1,
gradul de activare al conditiei pentru o valoare x=x* în
universul de discurs este exprimat prin
, multimea fuzzy asociata conditiei C1,
gradul de activare al conditiei pentru o valoare x=x* în
universul de discurs este exprimat prin
![]() (12.41)
(12.41)
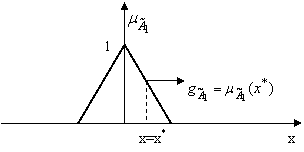
În figura 12.26 este ilustrat
grafic modul de calcul al gradului de activare.
Figura 12.26 Calculul gradului de activare
Pentru o regula completa
definita prin conditiile C1, C2, ..., Cp
carora li se asociaza multimile fuzzy ![]() ,
, ![]() , ....,
, ...., ![]() , definite pe universul de discurs x1, x2,
..., xp, se obtine:
, definite pe universul de discurs x1, x2,
..., xp, se obtine:
![]() , i=1, 2, ..., p (12.42)
, i=1, 2, ..., p (12.42)
Conditiile Ci sunt interpretate prin operatorul AND
![]() (12.43)
(12.43)
unde ![]() va reprezenta
functia de activare al variabilei de iesire, consecinta,
decizie a regulii determinate de expresia THEN.
va reprezenta
functia de activare al variabilei de iesire, consecinta,
decizie a regulii determinate de expresia THEN.
Sinteza deciziei, la nivelul unei reguli, este obtinuta în general prin algoritmul Mandami [12] care formal este scris sub forma:
 (12.44)
(12.44)
unde ![]() ,
, ![]() ,...,
,..., ![]() sunt multimi
fuzzy definite pe universul de discurs U al variabilei de iesire u.
sunt multimi
fuzzy definite pe universul de discurs U al variabilei de iesire u.

Figura 12.27 Calculul gradului de activare al unei reguli
Figura 12.28 ilustreaza tehnica de formare a deciziei în cadrul unei reguli. Pe întreaga baza, procedura este repetata pentru fiecare regula.

Figura 12.28 Generarea deciziei pentru regula j

În figura 12.29 este:
Figura 12.29 Generarea deciziilor pentru doua reguli.
prezentata generarea deciziilor
în doua reguli j si m, ![]() si
si ![]() reprezentând
multimile fuzzy corespunzatoare definite pe universul de discurs al
variabilei de iesire.
reprezentând
multimile fuzzy corespunzatoare definite pe universul de discurs al
variabilei de iesire.
 (12.45)
(12.45)
Implementarea numerica a bazei de reguli corespunde de fapt modului de tratare a operatorilor AND - OR. Cea mai des întâlnita modalitate de evaluare este cunoscuta sub numele "min - max" în care operatorii AND sunt evaluati prin functia "min", iar operatorii OR prin "max".
![]() (12.46)
(12.46)
![]()
Pentru exemplificarea ultimului operator, în figura 12.30 este prezentata functia max aplicata pe cele doua reguli j si m ilustrate în figura 12.29.

Figura 12.30 Generarea deciziei prin operatorul "max"
![]() (12.48)
(12.48)
Alte proceduri de implementare sunt definite ca "prod - max", unde:
![]() (12.49)
(12.49)
iar operatorul OR pastreaza forma (12.46).
De asemenea, se utilizeaza si forma "prod - suma" în care operatorul AND este tratata dupa relatia (12.47), iar OR prin:
![]() (12.50)
(12.50)
Pentru ilustrarea acestor proceduri se va utiliza baza de reguli prezentata în paragraful precedent, cu functiile de apartenenta ale celor doua variabile de intrare e, Δe si de iesire u.
Se va analiza metoda "min - max" ce
implementeaza conditiile logice AND si OR prin operatori min
si max, respectiv. În figura 12.31 este ilustrata grafic aceasta
metoda. Sunt analizate primele doua reguli ale bazei si este
exemplificata procedura pentru câteva valori particulare ale variabilelor
de intrare e si Δe, ![]() si
si ![]() .
.
Pentru Regula 1, ![]() determina un grad
de activare
determina un grad
de activare ![]() , pentru functia de apartenenta N:
, pentru functia de apartenenta N:
![]() (12.51)
(12.51)
iar ![]() , pentru functia de apartenenta P,
determina:
, pentru functia de apartenenta P,
determina:
![]() (12.52)
(12.52)
Conditia Regulii 1, "IF e este N AND Δe este P THEN u este Z" este tratata prin operatorul min:
![]()
Similar, pentru Regula 2 se obtine:
![]()
![]()
Cele doua functii de
activare ![]() ,
, ![]() determina
deciziile
determina
deciziile ![]() ,
, ![]() iar decizia
finala (dupa doua reguli) va fi conform relatiei (12.46),
iar decizia
finala (dupa doua reguli) va fi conform relatiei (12.46),
![]()
Aplicarea procedurii "prod - max" va determina câteva modificari cantitative
![]()
![]()
care se vor repercuta în noile forme
ale deciziilor ![]() ,
, ![]() si
corespunzator decizia finala
si
corespunzator decizia finala ![]() .
.

Figura 12.31 Implementarea regulilor 1
si 2 prin metoda "min-max"
În mod similar se obtine decizia prin algoritmul "prod - suma". Pentru comparare, în figura 12.32 sunt prezentate cele doua metode.

Figura 12.32 Analiza comparativa a metodelor
12.10 Defuzificarea
Paragrafele anterioare au abordat etapele principale în implementarea unui CLF, fuzificarea marimilor de intrare si procesarea algoritmului de conducere sub forma unei baze de reguli. În final, marimea de iesire este generata sub forma unei multimi fuzzy. Este evident ca se impune compatibilizarea acestei marimi cu procesul condus, deci este necesara reconversia marimii de iesire într-o marime crisp. Procedura aceasta este cunoscuta sub numele de defuzificare.
Defuzificarea reprezinta o etapa importanta în structura generala a proiectarii unui CLF si literatura de specialitate abunda în solutii [2, 3, 4, 5]. În cele ce urmeaza se vor prezenta câteva din tehnicile de implementare cele mai eficiente.
Defuzificarea prin "centru de greutate" este cea mai raspândita procedura de reconversie a deciziei fuzzy de la iesirea CLF într-o variabila crisp. Aceasta metoda se bazeaza pe evaluarea functiei de apartenenta a deciziei fuzzy dupa aceleasi reguli ca cele utilizate în calculul centrului de greutate din mecanica clasica. În acest mod se asociaza functiei de apartenenta a decizie variabilei de iesire o valoare crisp corespunzatoare.
Pentru fixarea ideilor, se va considera decizia D* reprezentata în figura 12.33. Functia de apartenenta a acestei decizii fuzzy este obtinuta din primele doua reguli ale aplicatiei discutate în paragraful precedent (figura 12.31).
Prin evaluarea "centrului de greutate" al ariei definita de functia de apartenenta a deciziei D* se obtine pe abscisa:
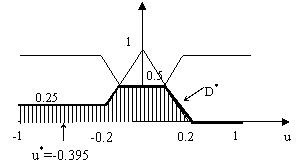
Figura 12.33 Defuzificarea deciziei D*
![]()
ceea ce reprezinta o masura crisp a deciziei fuzzy.
În cazul general, defuzificarea apeleaza la formula clasica a "centrului de greutate":
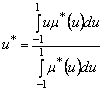
unde ![]() este functia de
apartenenta a deciziei finale obtinuta prin relatia (12.46),
numitorul reprezinta aria delimitata de functia de
apartenenta, iar numaratorul defineste momentul ariei.
În aceasta relatie s-a presupus ca universul de discurs U
este normalizat. Într-o forma mai generala, expresia (12.59) poate fi
rescrisa ca:
este functia de
apartenenta a deciziei finale obtinuta prin relatia (12.46),
numitorul reprezinta aria delimitata de functia de
apartenenta, iar numaratorul defineste momentul ariei.
În aceasta relatie s-a presupus ca universul de discurs U
este normalizat. Într-o forma mai generala, expresia (12.59) poate fi
rescrisa ca:

În mod curent este utilizata o procedura de discretizare

ceea ce permite, în cele mai multe cazuri, un calcul usor de implementat.
Pentru anumite cazuri particulare ale functiei de apartenenta, relatiile (12.59) - (12.61) pot capata anumite forme simplificate. De exemplu, daca iesirea este definita prin functii singleton, expresia (12.61) devine (figura 12.34):
![]()
unde:
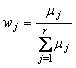

Figura 12.34 Defuzificarea pentru iesire de tip singelton
O interpretare si mai facila, desi evident destul de aproximativa, se poate obtine daca functia de apartenenta contine un maxim sau domenii maximale (figura 12.35).
![]()
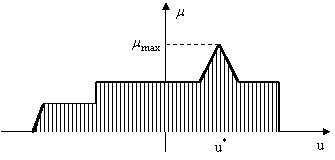
Figura
12.35 Defuzificarea prin valoarea maxima
12.11 Un exemplu de calcul
În paragrafele precedente a fost prezentata în detaliu metodologia de proiectare a unui CLF. Pentru a concretiza mai bine procedura si pentru a permite o mai buna familiarizare cu tehnicile de implementare, se va relua exemplul oferit de conducerea unui brat de robot (figura 12.25) cu baza de reguli prezentata în Tabelul 1 si functiile de apartenenta din figura 12.26. Se vor trata regulile de conducere prin metoda "min - max" pentru regimul de lucru definit prin:
![]()
![]()
Primele doua reguli sunt analizate în figura 12.31 si în continuare vor fi analizate celelalte sapte reguli ale bazei.
Astfel, Regula 3 impune algoritmul:
IF e este P AND Δe este P
THEN u este N
Gradul de activare al multimilor fuzzy se obtine în aceeasi maniera ca cea prezentata în paragraful 12.8:
![]()
![]()
iar functia de activare a iesirii, pe decizia N, va fi
![]()
ceea ce identifica decizia regulii, conform relatiei (12.45), ca multimea valorilor 0 în domeniul de discurs al variabilei de iesire:
![]() ,
, ![]()
În mod
similar sunt analizate celelalte reguli Regula 4, ..., Regula 9
obtinându-se deciziile sub forma multimilor fuzzy ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() , respectiv.
, respectiv.
Decizia finala, pentru variabilele de
intrare ![]() se obtine
dupa formula (12.46):
se obtine
dupa formula (12.46):
![]()
Întreaga procedura este ilustrata în figurile 12.36 si 12.37.
|
N |
|
Z |
|
P |
|
ge=0 |
|
|
|
|
|
|
|
e |
|
|
|
fN6=0 |
|
|
|
|
|
|
|
u |
|
N |
|
Z |
|
P |
|
|
|
|
|
|
|
g |
|
|
|
N |
|
Z |
|
P |
|
|
|
|
|
e=-0.3 |
|
min |
|
N6* |
|
|
|
|
|
|
|
|
|
N |
|
Z |
|
P |
|
ge=0.75 |
|
|
|
|
|
|
|
e |
|
N |
|
Z |
|
P |
|
ge=0.75 |
|
|
|
|
|
e |
|
N |
|
Z |
|
P |
|
g |
|
|
|
|
|
|
|
|
|
N |
|
Z |
|
P |
|
fP7=0 |
|
|
|
|
|
u |
|
min |
|
P7* |
|
Reg 7 |
|
Reg 6 |
|
|
|
|
|
|
|
|
|
N |
|
Z |
|
P |
|
ge=0.25 |
|
|
|
|
|
|
|
e |
|
N |
|
Z |
|
P |
|
|
|
|
|
e |
|
N |
|
Z |
|
P |
|
g |
|
|
|
|
|
|
|
|
|
N |
|
Z |
|
P |
|
fZ5=0.25 |
|
|
|
|
|
|
|
u |
|
min |
|
Z5* |
|
Reg 5 |
|
|
|
|
|
|
|
|
|
N |
|
Z |
|
P |
|
|
|
|
|
|
|
e |
|
N |
|
Z |
|
P |
|
ge=0 |
|
|
|
|
|
e |
|
N |
|
Z |
|
P |
|
g |
|
|
|
|
|
|
|
|
|
N |
|
Z |
|
P |
|
fN3=0 |
|
|
|
|
|
|
|
u |
|
min |
|
N3* |
|
Reg 3 |
|
|
|
N |
|
Z |
|
P |
|
ge=0.75 |
|
|
|
|
|
|
|
e |
|
|
|
fP4=0.5 |
|
|
|
|
|
|
|
u |
|
N |
|
Z |
|
P |
|
|
|
|
|
|
|
g |
|
|
|
N |
|
Z |
|
P |
|
|
|
|
|
min |
|
P4 |
|
Reg 4 |

N Z ge=0.25 e N Z P e N Z P g N Z P u Z P ge=0 e fZ9=0 u N Z P g N Z P e=-0.3 min Z9 Reg 8 Reg 9

Figura
12.36 Implementarea bazei de reguli - conducerea
unui brat robot
u*=-0.22 u D*

Figura 12.37 Defuzificarea decizie -
conducerea unui robot
12.12 Analogia între CLF si regulatoarele conventionale PD, PI, PID
Exemplul analizat în paragraful precedent ilustreaza modul de calcul al variabilei de iesire u în functie de eroarea e(k)si variatia erorii Δe(k), deci determina o lege de conducere de forma
![]()
O astfel de lege de conducere este similara cu cea stabilita în regulatoarele conventionale de tip PD care genereaza un control sub forma unei combinatii între o componenta de tip proportional si una de tip derivativ [10, 11]:
![]()
unde kP si kD sunt parametrii regulatorului PD.
Prin analogie, o lege de conducere obtinuta într-un CLF, de forma (12.66) se va numi CLF - PD.
Daca regulile unui CLF nu genereaza valoarea u(k), ci variatia marimii de iesire Δu(k):
![]()
deci se implementeaza o lege de conducere generala de forma
![]()
atunci aceasta lege se poate asocia cu cea oferita de un regulator conventional de tip PI descris prin relatia:
![]()
unde kP si kI sunt parametrii regulatorului PI.
În acest sens, un CLF a carei baza de reguli defineste un algoritm de forma (12.69) se va numi de tipul CLF - PI.
Procedura poate fi extinsa pentru legi de conducere mai complexe. De exemplu, daca legea unui CLF este generata sub forma:
![]()
unde:
![]()
ea va fi de tipul PID, întrucât este similara cu cea obtinuta de regulatorul conventional cu acelasi nume:
![]()
Este evident ca o astfel de lege
impune în CLF o baza de reguli mai complexa, definita pe
variabilele ![]()
![]()
![]()
IF
![]()
![]()
![]()
THEN ![]()
O forma modificata a legii (12.12.6) care poate fi acceptata în definirea unui CLF - PID poate fi de forma:
![]()
care corespunde regulatorului PID discret:
![]()
Desigur, pot fi adoptate si alte legi de conducere, cu algoritmi mai sofisticati, dar este evident ca o crestere a numarului de variabile de intrare (antecedente) în structura regulilor, determina o implementare extrem de dificila si în multe cazuri cu totul nepractica. Din acest motiv, introducerea a mai mult de doua variabile de intrare în structura regulilor este acceptata numai în conditii de performante cu totul speciale.
12.13 Consideratii asupra universului de discurs
În general, universul de discurs al variabilelor de intrare si de iesire la un CLF este reprezentat de dreapta numerelor reale. În practica, fiecare univers este restrictionat la un interval bine definit între o valoare maxima si una minima în conformitate cu rangul marimilor fizice.
Sa luam, pentru exemplificare, conducerea unui brat robot (figura 12.25) unde:
![]()
Universul de discurs al erorii va fi definit practic de valorile maximale si minimale ale variabilelor de pozitie prescrise xd si masurate x.
![]()
![]()
![]()
În mod analog se vor defini universele de discurs ale variatiei erorii si ale variatiei de iesire (de control) u:
![]()
![]()
![]()
![]()
Este evident ca în functie de problema de conducere abordata, domeniile universurilor de discurs pot fi extrem de diverse. Totusi, pentru simplificarea tratarii si unificarea metodologiei de proiectare, este de preferat sa se opereze pe universuri de discurs normalizate.
Pentru exemplificare se va considera
ca variabilele e(k), Δe(k) si u(k) opereaza pe domeniile ![]()
![]()
![]()
![]()
![]()
![]()
Pentru a transforma domeniile de operare ale variabilelor de intrare masurate e(k), Δe(k) în universul de discurs normalizat se utilizeaza factori de scala [10, 11]:
![]()
![]()
Acesti coeficienti vor transforma valorile reale masurate ale intrarilor în CLF, e(k), Δe(k), în valorile e*(k), Δe*(k) din universul normalizat:
![]()
![]()
unde:
![]()
![]()
Algoritmul bazei de reguli se va aplica marimilor normalizate si va permite dupa defuzificare, obtinerea unei variabile de iesire din universul corespunzator normalizat:
![]()
Implementarea completa a CLF-ului impune generarea iesirii în universul real de activare, deci este necesara o "denormalizare" printr-un factor de scala corespunzator:
![]()
![]()
ceea ce determina revenirea
variabilei de iesire în domeniul ![]()
În general, universul normalizat poate fi identic cu un rang real de operare al unei variabile, dar, pentru cele mai multe aplicatii, acesta coincide cu intervalul închis [-1,1].
Factorii de scala joaca un rol extrem de important în proiectarea unui CLF. Este evident ca scalarea erorii si a variatiei acesteia înseamna efectiv o transformare a spatiului de stare ceea ce va determina o modificare automata a performantelor. În literatura de specialitate [8, 9, 10] sunt mentionate urmatoarele reguli ce se impun în selectia factorilor de scala:
Alegerea unor valori mari ale factorilor ke determina erori stationare mici, timp de crestere mic si suprareglaj ridicat, în timp ce valori mici ale lui ke determina o comportare opusa;
Valori mari ale lui kd determina o convergenta rapida;
Timpul de crestere este ridicat pentru valori mici ale factorului ku.
12.14 Metodele Takagi - Sugeno - Kang (TSK)
Modelele fuzzy discutate anterior se bazau pe reguli în care atât partea conditionala cât si cea decizionala cuprindea multimi fuzzy
Regula i: IF CONDIŢIA C1
AND CONDIŢIA C2 AND ... ![]()
THEN DECIZIA Di ![]()
Astfel de modele nu contin nici o forma explicita a functiei obiectiv si sunt cunoscute frecvent sub denumirea de modele Mandani.
O alta modalitate de tratare, atragatoare în cazul sistemelor mari si complexe, este oferita de modelul Takagi - Sugeno - Kang (TSK) în care iesirea, decizia sistemului este obtinuta dupa o lege non-fuzzy, ca o functionala pe variabilele de intrare.
Regula i: IF x1 este C1i
AND x2 este C2i AND ... ![]()
THEN ![]()
![]()
Marele avantaj al acestui model rezida în posibilitatea de tratare a sistemelor complexe prin decompozitia acestora în subsisteme mai simple, uneori chiar, subsisteme liniare. De asemenea, o alta posibilitate de abordare consta în descompunerea spatiului de stare al sistemului în subspatii disjuncte si identificarea modelelor dinamice pentru fiecare subspatiu. Iesirea finala este obtinuta printr-o compunere logica a iesirilor fiecarui subspatiu.
În cele mai dese cazuri, partitionarea spatiului de stare este astfel realizata încât iesirea sa poata fi generata sub forma unor modele liniare.
Regula 1: IF x1 este C11 AND ... AND xn este Cn1
THEN ![]()
Regula p: IF x1 este C1p AND ... AND xn este Cnp
THEN ![]()
În ceasta baza de reguli, Cij (j=1,p), (i=1,n) sunt multimi fuzzy pe spatiul de stare al sistemului X1, X2, ..., Xn iar x1, x2, ..., xn sunt valori crisp ale variabilelor de intrare (stare). Partea decizionala a regulilor poate fi considerata ca modele liniare ce definesc variabilele de iesire u1, u2, ..., up (marimi crisp) în functie de variabilele de intrare (stare), variabile crisp. Iesirea globala u a întregului model TSK se obtine printr-o medie ponderata a iesirilor crisp ui pentru fiecare subsistem liniar. Considerând gradul de activare al fiecarei conditii Cij:
![]()
iar functia de activare la nivelul unei reguli:
![]()
iesirea generala va fi:

Daca iesirea fiecarei
reguli este o functie neliniara ![]()
Modelul TSK poate fi utilizat pentru implementarea unui CLF de tipul PI, PD, sau PID. De exemplu, un CLF - PI poate fi modelat prin urmatoarea baza de reguli:
Regula 1: IF e(k) este C11 AND Δe(k) este C21
THEN ![]()
Regula p: IF e(k) este C1p AND Δe(k) este C2p
THEN ![]()
Iesirea CLF va fi:
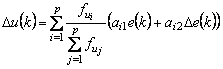
unde ![]()
Analogia acestui model cu un regulator conventional PI permite identificarea parametrilor regulatorului:
![]()
deci:
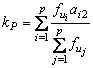
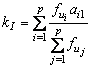
12.15 Controlul cinematic diferential prin CLF
Dupa cum este bine cunoscut în literatura de specialitate [6], controlul cinematic diferential utilizeaza modelul diferential al unui robot, model ce permite calculul diferential dX al coordonatelor operationale (variabile ce definesc pozitia în spatiul de lucru) în functie de variatia dq a coordonatelor generalizate (variabile asociate fiecarei articulatii mecanice). Analitic, aceasta dependenta este scrisa printr-o matrice Jacobian, în forma
![]()
Structura clasica a unui control cinematic diferential este prezentata în figura 12.38.
Asa
dupa cum se cunoaste, punctul slab al unei astfel de conduceri îl
constituie calculul inversei matricei Jacobian, calcul ce nu poate fi realizat
off-line datorita dependentei coeficientilor matricei de
parametrii qi. Cu toate ca în literatura s-au dezvoltat o
serie de metode care permit calculul rapid al lui ![]()
J-1(q) f(q) xdi qi xi

Figura 12.38 Controlul cinematic diferential
conventional
În cele ce urmeaza, se va analiza o solutie de control cinematic diferential utilizând un CLF care va permite calculul inversei matricii Jacobian adoptând euristic o baza de reguli corespunzatoare.
Este evident ca atât structura conventionala cât si cea utilizând logica fuzzy trebuie sa urmareasca acelasi criteriu de calitate, minimizarea erorii sistemului de conducere.
CLF f(q) xdi qi xi

Figura 12.39 Control cinematic diferential cu CLF
Într-o scriere generala, eroarea poate fi definita [8], [9] astfel:
![]()
unde Xd este vectorul de pozitie dorit în spatiul cartezian. Legea de conducere care se va introduce trebuie sa determine variatii Δq care sa permita micsorarea erorii. O solutie simpla se bazeaza pe utilizarea unei metode de tip "gradient":
![]()
unde η este un factor de
proportionalitate ales convenabil, ![]()
![]()
astfel încât variatiile Δq vor fi date de legea:
![]()
Se poate arata usor ca adoptarea unei legi de conducere de tipul (12.107) ofera solutii bune pentru un sistem de tipul celui prezentat în Figura 12.39, o astfel de conducere determinând convergenta la zero a erorii (12.104)
![]()
Pentru justificarea acestei solutii se va utiliza metoda a 2-a a lui Liapunov si se va defini o functionala Liapunov de forma:
![]()
Derivata acestei functionale, de-a lungul traiectoriei sistemului va fi:
![]()
Aproximând derivata ![]()
![]()
unde T este timpul de esantionare, se obtine:
![]()
sau:
![]()
dar, cu exceptia cazurilor în
care matricea ![]()
![]()
ceea ce confirma convergenta la zero a erorii e din (12.104).
Pentru ilustrarea metodei vom analiza sistemul de conducere pentru un robot planar cu doua articulatii (figura 12.40)
Coordonatele operationale sunt:
![]()
iar matricea Jacobian va fi:
![]()
Pentru o eroare de forma:
![]()
se impune o lege de conducere de forma (12.107) care va fi implementata într-un CLF:
![]()
Y X x (x,y)=X q2 q1

![]()
Figura 12.40 Modelul unui robot planar cu 2 articulatii
sau într-o forma simplificata:
![]()
![]()
unde Jij sunt componentele matricei Jacobian iar ex, ey reprezinta erorile pe cele doua coordonate operationale.
Pentru transpunerea celor doua relatii (12.120), (12.121) într-o baza de reguli se vor adopta functiile de apartenenta din figura 12.41.
Numarul mare de variabile (de
intrare) antecedent în definirea regulilor ![]()
De exemplu, prima regula se va formula astfel:
Regula 1: IF ex este N AND J11 este N AND ey este P AND J21 este P
THEN Δq1 este PM.
-E -0.1E 0.1E +E N P Z ex, ey Iij -I -0.2I 0.2I +I N P Z -0.6Q 0.2Q 0.2Q +0.6Q Nm Pm Z -Q Q PM NM

Figura 12.41 Functii de apartenenta
|
J21 J11 ey ex |
N |
Z |
P |
|||||||
|
N |
Z |
P |
N |
Z |
P |
N |
Z |
P |
||
|
P |
P |
PM |
Pm |
ZP |
Pm |
Pm |
Pm |
ZP |
Pm |
PM |
|
Z |
Pm |
ZN |
Nm |
ZN |
ZP |
ZP |
Nm |
ZN |
Pm |
|
|
N |
ZN |
Nm |
NM |
Nm |
Nm |
Nm |
NM |
Nm |
ZN |
|
|
Z |
P |
Pm |
ZN |
Nm |
ZN |
ZN |
ZP |
Nm |
ZP |
Pm |
|
Z |
Pm |
ZP |
Nm |
Nm |
ZN |
ZP |
Nm |
ZP |
Pm |
|
|
N |
ZN |
ZN |
Nm |
ZN |
ZN |
ZP |
Nm |
ZP |
Pm |
|
|
N |
P |
ZP |
Nm |
NM |
Nm |
Nm |
Nm |
NM |
Nm |
ZN |
|
Z |
Pm |
ZN |
Nm |
ZN |
ZN |
ZN |
Pm |
ZP |
Pm |
|
|
N |
PM |
Pm |
ZP |
Pm |
Pm |
Pm |
ZP |
Pm |
PM |
|
Tabelul 12.3 Baza de reguli
Toate celelalte reguli se vor formula într-o maniera similara, variabila de iesire Δq1 obtinându-se din functiile de apartenenta prezentate în figura 12.41.
12.16 Proiectarea unui CLF ca un sistem ca structura
variabila
Paragrafele precedente au pus în evidenta tehnicile generale de implementare a unui CLF si asimilarea sa cu regulatoare conventionale PD, PI, PID. Metodologia de proiectare si implentare a subliniat ideea ca un CLF este un controler robust care permite obtinerea unor performante de conducere satisfacatoare în conditiile unei cunoasteri, deseori insuficienta, a modelului matematic al sistemului. De fapt, ideea agreata în aceasta proiectare consta în pozitionarea spatiului starilor si adoptarea unor legi de conducere PI sau PD în fiecare spatiu, parametrii de conducere fiind modificati la comutarea dintr-un subspatiu în altul. Deci, în esenta, un CLF este un sistem cu structura variabila.
Pentru a ilustra aceasta metoda se va considera modelul dinamic definit de ecuatia:
![]()
prezentat în figura 12.42.
|
CSV |
|
SISTEM |
|
|
|
|
|
|
|
|
 |
În ecuatia (12.122),
functiile ![]()
![]()
Starea dorita a evolutiei este definita ca:
![]()
iar eroarea de urmarire va fi:
![]()
sau:
![]()
Daca se considera suprafata:
![]()
unde![]()
![]()
Suprafata:
![]()
este un subspatiu de dimensiune
(2n-1) si este numita suprafata de comutatie.
Aceasta suprafata divide spatiul în doua regiuni ![]()
![]()
În cazul n=1, ![]()
![]()
![]()
Un controler cu structura variabila CSV (figura 12.43) va conduce sistemul spre suprafata de comutare într-un timp finit si constrânge sistemul sa ramâna pe suprafata de comutare.
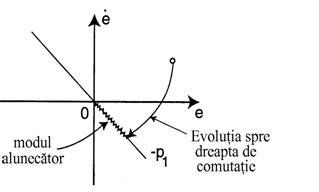
Figura 12.43 Traiectoria într-un sistem cu
structura variabila
Când sistemul opereaza pe suprafata (dreapta) de comutare se spune ca acesta evolueaza în mod "alunecator" (sliding).
Una din cele mai simple legi de control poate fi:
![]()
dar legea de control poate fi mai complexa în functie de complexitatea sistemului.
Se va analiza, în continuare, conducerea unui brat mecanic al unui sistem descris prin ecuatia:
![]()
si se vor considera ![]()
![]()
![]()
![]()
![]()
![]()
Din relatia (12.129) se obtine:
![]()
![]()
si, din (12.132), (12.133), expresia (12.131) devine:
![]()
unde:
![]()
Se va presupune ca legea de control va avea forma:
![]()
unde c este o ![]()
Brat robot CLF Controler
conventional u1=-cs+H

Figura 12.44 Conducerea unui brat-robot cu CLF
si controler conventional
Nm Pm Z PM NM e
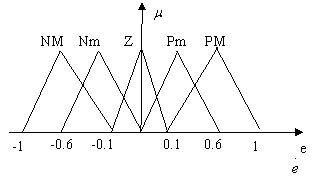
Figura 12.45 Functiile de apartenenta
pentru e,![]()
Nm Pm Z NM PM uF
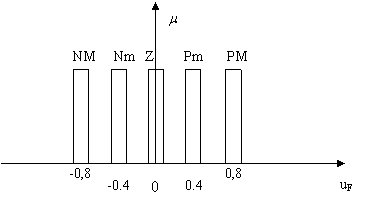
Figura 12.46 Functiile de apartenenta pentru iesirea uF
Pentru a determina conditiile de stabilitate ale sistemului, se va considera metoda a 2-a a lui Liapunov. Se va utiliza o functie Liapunov de forma:
![]()
deci:
![]()
si din (12.134) se obtine:
![]()
Conditia de stabilitate impune
![]()
deci:
![]()
![]()
Pentru implementarea CLF, se vor
adopta functiile de apartenenta pentru ![]()
![]()
Notatiile folosite NM, Nm,Z,Pm, PM desemneaza etichetele lingvistice NEGATIV MARE, NEGATIV MEDIU, ZERO, POZITIV MEDIU, POZITIV MARE, respectiv. Pentru functia de iesire, se vor adopta, cu aceleasi etichete, functii singleton (Figura 12.46).
Baza
de reguli va implementa relatia (12.142) si este prezentata
sintetic în Tabelul 12.4. Se remarca ca deasupra diagonalei ![]()
![]()
|
e e |
NM |
Nm |
Z |
Pm |
PM |
|
PM |
Z |
Nm |
Nm |
NM |
NM |
|
Pm |
Pm |
Z |
Nm |
Nm |
NM |
|
Z |
Pm |
Pm |
Z |
Nm |
Nm |
|
Nm |
PM |
Pm |
Pm |
Z |
Nm |
|
NM |
PM |
PM |
Pm |
Pm |
Z |
Tabelul 12.4 Baza de reguli
Regulile tabelei vor avea urmatoarea interpretare:
Regula 1: IF ![]()
![]()
THEN ![]()
Regula 2: IF ![]()
![]()
THEN ![]()
Regula 16: IF ![]()
![]()
THEN ![]()
|