STABILITATEA SI MANIABILITATEA AUTOVEHICULULUI

STABILITATEA sI MANIABILITATEA AUTOVEHICULULUI

9.1.Stabilitatea autovehiculului

fata de cazul ideal rotile puntii din spate sunt suprafrânate - se blocheaza - iar cele din fata sunt subfrânate;

fata de cazul ideal rotile puntii din fata sunt suprafrânate - se blocheaza - iar cele din spate sunt subfrânate.

Din punct de vedere al stabilitatii automobilului primul caz reprezinta un comportament supravirator, instabil pe traiectoria rectilinie a automobilului, iar cel de-al doilea caz un comportament de subvirare, autostabilizant pe traiectoria rectilinie a automobilului.

Din evaluarea celor doua comportamente ale automobilului frânat si anune instabil daca rotile din spate se blocheaza inaintea cel din fata si autostabilizant pe traiectoria rectilinie daca rotile din fata se blocheaza înaintea celor din spate, în constructia sistemului de frânare se utilizeaza, fara nici o exceptie, un dispozitiv, cel putin de tipul limitatoarelor de frânare, pentru corectarea fortei de frânare la roti. Rolul functional al unui astfel de dispozitiv este acela de a evita ca la frânarea intensiva - de urgenta - sa se produca blocarea rotilor din spate înaintea celor din fata, respectiv exclude posibilitatea instalarii caracterului supravirator.

Datorita efectelor defavorabile pe care blocarea rotilor le are asupra eficacitatii frânarii, stabilitatii si maniabilitatii autovehiculului, precum si asupra uzurii pneurilor, s-au dezvoltat solutii tehnice de dispozitive antiblocare, care împiedica blocarea rotilor indiferent de momentul de frânare aplicat si de coeficientul de aderenta.

Daca se defineste forta specifica de frânare a autovehiculului ca raport dintre suma fortelor de frânare la punti si greutatea totala a autovehiculului de forma:

(9.30)

unde:

Folosind notatiile: , si , in conditiile în care iar deceleratia relativa are valoarea maxima d_f =j (rel.7.1), relatiile (9.31) si (9.32) devin:

(9.33)

din care prin eliminarea coeficientului de aderenta j se obtine ecuatia de gradul al doilea de forma:

(9.34)

care reprezinta ecuatia unei parabole cunoscute sub numele de "paraboila distributiei ideale a fortei de frânare" deoarece defineste marimile maxime ale fortelor specifice de frânare la rotile autovehiculului dezvoltate simultan la limita de aderenta, când se obtine deceleratia maxima posibila sau deceleratia ideala .

Pentru o situatie bine determinata când se cunosc reprezentând grafic relatia (9.34) cu în abscisa si in ordonata, se obtine o parabola care trece prin origine si intersecteaza axele in punctele de coordonate si (fig.9.3)

Fig.9.3 Parabola distributiei ideale a fortelor de frânare

Fiecarui punct al parabolei ii corespunde un anumit coeficient de aderenta, care se poate preciza ducând în acest punct o paralela la bisectoarea a doua a axelor si citind valoarea corespunzatoare la intersectia cu una din axele de coordonate.

Rezulta ca pentru a se realiza frânarea optima, raportul fortelor de frânare la punti trebuie sa fie variabil.

Timând seama de relatia (9.30) expresia deceleratiei relative devine:

(9.35)

cu ajutorul careia din relatiile (9.31) si (9.32) se obtine:

(9.36)

j , determina un fascicul de drepte care trece prin punctul de coordonate . Pentru un autovehicul cu o anumita sarcina, la care se cunosc coordonatele centrului de greutate si se deplaseaza pe o anumita cale, fortele specifice de frânare si sunt dependente de forta de apasare pe pedala de frâna.

O dreapta împarte planul în doua regiuni, una pozitiva si una negativa. Daca se considera dreapta de ecuatie , atunci una din regiuni este cea pentru care D₁<0, iar a doua regiune este cea pentru care D₁>0.

Reprezentarea grafica a dreptelor D_I si D_II, ale caror ecuatii sunt date de relatiile (9.36) si respectiv (9.37), in sistemul de coordonate , imparte planul in patru domenii dupa cum urmeaza:

- domeniul I în care: D_I>0, D­_II>0;

- domeniul II în care: D_I>0, D­_II<0;

- domeniul III în care: D_I<0, D­_II>0;

- domeniul IV în care: D_I<0, D­_II<0;

Acestor domenii, figura 9.4, le corespund urmatoarele situatii pentru starea de frânare a rotilor autovehiculului:

I - rotile din fata si din spate ruleaza fara tendinta de blocare, deci au alunecari relative în zonele de stabilitate;

II - rotile din fata ruleaza fara blocare iar cele din spate se blocheaza;

III - rotile din fata se blocheaza iar cele din spate ruleaza fara blocare;

IV - rotile ambelor punti se blocheaza.

Fig.9.4 Dreptele de echiaderenta

9.2. Maniabilitatea autovehiculelor

Virajul unui autovehicul este considerat corect daca rotile directoare ruleaza fara alunecari laterale. Pentru aceasta este necesar ca toate rotile automobilului sa descrie cercuri concentrice în jurul unui singur punct, numit centru efectiv de viraj (punctul O din fig.9.3). În cazul automobilelor cu 4 roti centrul efectiv de virare este situat la intersectia dintre axa puntii spate si axele rotilor directoare. Pentru aceasta trebuie ca roata de directie interioara virajului sa fie rotita cu un unghi de bracare mai mare decât unghiul de rotire a rotii exterioare virajului (θ₁>θ₂).

Conditia de virare corecta, adica de înscriere în viraj a autovehiculului fara ca rotile de directie sa derapeze lateral, se obtine când toate punctele autovehiculului descriu cercuri concentrice in O, (fig.9.5), respectiv din triunghiurilor OAD si OBC, pot fi determinate urmatoarele relatii:

si (9.31.)

Facând diferenta celor doua egalitati se obtine expresia:

(9.32.)

în care L reprezinta ampatamentul autovehiculului si b distanta dintre pivotii rotilor directoare.

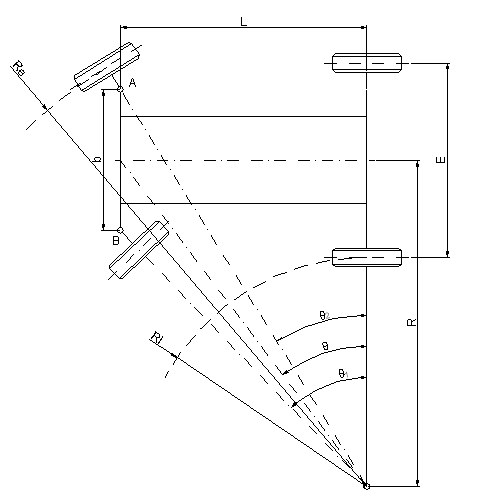
Fig.9.5 Schema virarii corecte a autovehiculului cu roti rigide

Dintre parametrii geometrici ai virajului prezinta interes razele minime de virare, obtinute atunci când se efectueaza virajul cu unghiurile maxime de bracare.

Din triunghiurile OAD si OBC, fig.9.5 se pot scrie relatiile :

- pentru raza exterioara de virare:

; (9.33.)

- pentru raza interiara de virare:

(9.33.)

Din cele prezentate privind stabilitatea si maniabilitatea autovehiculului nu s-a tinut seama de elasticitatea transversala a pneurilor, care influenteaza traiectoria reala, deoarece, prin deformarea laterala a pneului, poate apare o abatere de la directia initiala de deplasare.

Daca asupra autovehiculului actioneaza o forta de deviere laterala F_y determinata de forta centrifuga, de vântul lateral, sau de înclinarea transversala a caii de rulare, datorita elasticitatii laterale a pneului roata deviaza de la directia initiala de deplasare cu un unghi δ, care este denumit unghi de deviere laterala sau unghi de deriva. Marimea acestui unghi depinde de marimea fortelor care actioneaza asupra rotii de directie, de constructia pneului, de marimea presiunii interioare a aerului din pneu. Valorile maxime ale unghiului de deriva se afla în intervalul δ = 12 - 18⁰, dupa care poate aparea deraparea autovehiculului.

Componenta F_iy a fortei centrifuge (fig.9.6), la deplasarea în viraj, determina aparitia unghiurilor de deriva δ₁ la rotile puntii fata, respectiv δ₂ la rotile puntii spate, care influenteaza traiectoria miscarii în raport cu traiectoria comandata de conducatorul autovehiculului. Ca urmare a elasticitatii laterale a pneurilor centrul instantaneu de virare se deplaseaza din punctul O în punctul O_δ, aflat la intersectia perpendicularelor pe vectorii vitezelor rotilor fata, V_a1 si din spate, V_a2.

Fig.9.6 Schema virarii autovehiculului cu roti elastice

Distanta dintre centrul instantaneu de virare si axa longitudinala de simetrie a autovehiculului se numeste raza de virare si se noteaza cu R_δ.

Daca δ₁ = δ₂ raza de viraj a autovehiculului este aceeasi ca si în cazul în care acesta ar avea roti rigide (R = R_δ).În acest caz se spune ca autovehiculul are virare normala sau neutra.

Daca δ₁ > δ₂ razele de viraj nu mai sunt egale (R_δ > R) iar autovehiculul are capacitatea de viraj insuficienta sau este subvirator. În acest caz, la deplasarea autovehiculului în viraj, pe curba de raza R, rotirea volanului trebuie sa se faca cu un unghi mai mare decât se face la virarea neutra.

Daca δ₁ < δ₂ razele de viraj nu mai sunt egale (R_δ < R) iar autovehiculul are capacitatea de viraj excesiva sau este supravirator, deoarece pentru deplasarea pe curba de raza R, volanul trebuie rotit la un unghi mai mic decât în cazul virarii neutre.

La deplasarea rectilinie a autovehiculului., când rotile de directie nu sunt bracate si sunt paralele cu directia de înaintare, la aparitia unor forte de deviere laterala, apare tendinta ca autovehiculul sa devieze de la directia rectilinie si sa înceapa sa vireze, fara comanda primita de la conducator. În acest caz conducatorul trebuie sa intervina si sa roteasca de volan, într-un sens sau altul, pâna la aducerea autovehiculului pe directia dorita de deplasare.

În cadrul proiectului, la acest capitol, trebuie verificat, prin calcul si grafic, daca autovehiculul proiectat respecta legea virarii corecte, data de relatia 9.31, adica daca se înscrie în curba fara derapari sau alunecari ale rotilor directoare. Pentru aceasta trebuie cunoscute dimensiunile geometrice ale automobilului, si distanta dintre axele pivotilor De asemenea trebuie calculate raza exterioara R_e si raza interioara R_I, cu ajutorul relatiilor 9.33, cunoscând ca valorile maxime ale unghiurilor de bracare ale rotilor directoare sunt cuprinse între 30-35 grade. Razele minime de virare calculate trebuie comparate cu cele ale solutiilor similare.