STUDIUL VARIATOARELOR DE C.C. , AL PRINCIPALELOR TOPOLOGII FOLOSITE LA STUDIUL CONVERSIEI C.C.

STUDIUL VARIATOARELOR DE C.C. , AL PRINCIPALELOR TOPOLOGII FOLOSITE LA STUDIUL CONVERSIEI C.C.

-> topologii de contactoare statice cu comanda sustinuta

-> -------------"----- ----- ------- cu regim de functionare in impulsuri .

CONVERTOR /VARIATOR de c.c.-c.c. cu raport de transformare subunitar - conv. de tip BUCK

1. INTRODUCERE

Acest variator produce la OUT o tens. medie U₂ mai mica decit tens. de IN continua aplicata . Principala aplicatie a conv. de tip BUCK este in sursele cu functionare in comutatie (U₂- trebuie ct.) si in actionarile electrice la care pt. modif. turatiei motorului de c.c. (U₂-trebuie modificat). La sursele cu functionare in comutatie , variatia tens. de IN U₁ nu trebuie sa determine la OUT variatia tens. U₂ .

Topologia de baza a unui astfel de convertor

Filtrul de OUT care are in componenta si inductanta de acumulare care are rolul de a fi acumulator de energie , si a doua - FTJ care precede sarcina propriu-zisa .

Caracteristica amplitudine-frecventa :

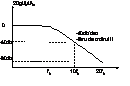In aceasta situatie f₀ trebuie plasata la stg . fata de frecv . de esantionare 1/T pt. ca celelalte componente spectrale sa fie rejectata .

NOTA : in analiza pe care o efectuam asupra conv. BECK , vom considera C de val. f. mare , aceasta fiind o situatie care este realizata pt. sursele cu functionare in comutatie , unde este necessar ca U₂=ct. In continuare i_L=i₂=ct. (pt. ca C cur. se scurge numai prin R.) .

2 In regimul stationar de conductie continua >pp. faptul ca circ. a fost alimentat ; nu iau in considerare procesele tranzitorii de conectare a tens. U₁ , aceste fenomene fiind diferite de cele de regim stationar .

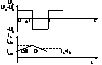
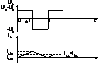La intrarea in conductie a CS , sursa U1este conectata la circ . de sarcina si se acumuleaza energie in L . La blocarea CS-ului , datorita inversarii pol. la bornele lui L se deschide dioda D si energia acumulata in L este retrocedata circ. de sarcina .In cele ce urmeaza vom consideraca I₁=I₂ , i₂(t)=I₂ , u₂(t)=U₂ , componentele alternative inchizindu-se prin C.

sau

(U₁-U₂)*D*T-U₂ (1-D)*T=0 => U₂/U₁=D .

Neglijind pierderile de putere in fen. de conversie -> P1=P2 - puterea medie furnizata de circ. de IN = cu puterea furnizata de circ. de OUT : U₁*I₁=U₂*I₂ => U₁/U₂=I₂/I₁=1/D .

In modul de conductie continua prin inductanta , convertorul este echiv. cu un transformator de c.c. unde rap. de transfer [0,1] prin intermediul factorului de umplere D. Se obs. ca daca cur. mediu de IN I₁ urmareste relatia de transfr. ,variatia curentului i₁ este cuprinsa intre I_LM si I_Lm la fiecare comutare on-off a CS. Un FTJ la IN poate fi necesar pt. a elimina armonicile nedorite de curent .Acest filtru este cu atit mai necesar cu cit cur. furnizat de sursa de IN este discontinuu.

In acest mod de conductie caracteristica externa normata nu depinde de curentul I₂ (cur. prin sarcina ).

3. Regimul de conductie discontinua : (reg. limita)

Diagramele de variatie a tens. si curentului :

In acest regim periodic curentul prezinta treceri periodice prin 0.

a). Regimul limita de functionare considerind U₁=ct. , U₂=reglabil .

I_LL=I_LM/2=U_L*DT /2L=DT*(U₁-U₂)/2L .

In intervalul ON pot scrie aceste relatii : I_LL=DT*U₁*(1-D)/2L .

Val. medie la limita conductiei de curent :

I_LLmax =I_LL |_D=0.5=T*U₁/8L

sau I_LL=4*I_LLmax*D*(1-D).

EOF
(F1P1C2) EI CURS 3 continuare la 2

STUDIUL CONVERTOARELOR DE TIP BUCK (continuare)

B. Regimul de conductie discontinua avind tensiunea de iesire    U₂=ct .

In aplicatiile cu surse de comutare U₁=tensiunea de IN poate varia ca efect al variatiei tens . de alimentare , dar U₂=tens. de OUTeste mentinuta ct. prin ajustarea factorului de conductie D in toata plaja de variatie a curentului prin sarcina . De aceea in acest caz se obisnuieste sa se prezinte o caracteristica : D= f( I₂/I_LLmax) . Inainte de aceasta vom studia si regimul limita .

Din U₁=U₂/D se obt . : I_LL=T*U₂*(1-D)/2L (1) arata ca daca tens. U₂ este mentinuta ct . val. medie max . a curentului I_LL apare ipotetic pt . D=0 .

I_LLmax=T*U₂/2L (2). Din rel. (1) si (2) se obtine :

I_LL=(1-D)*I_LLmax (3) D=(1-I_LL)/I_LLmax ec. unei drepte =locul geometric al punctelor pt. care convertorul se afla la limita conductiei de curent. Pt . modul de conductie discontinua , utilizind I₂ U₂ D D D₁ D₁ L se obtine :

D =U₂/U₁ * (I₂ / I_LLmax / (1-U₂/U₁))^1/2 (4).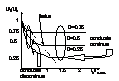Caracteristica raportului de conductie D a fost reprez. functie de I₂ normat avind ca reper U₂/U₁.

In conductia continua D nu depinde de val. curentului prin sarcina . Aici trebuie stabilizata functionarea sursei de alimentare . Probabilitatea ca sursa sa oscileze in aceasta zona este cea mai mica .

5. Elemente de performanta si proiectare

Introducere : In analiza anterioara condensatorul de iesire a fost suficient de mare a.i. s-a putut considera ca tens. de OUT este ct. In practica acest lucru nu e realizabil , iar pt. o val. finita a condensatorului de OUT , riplul tens. U₂ pote fi calculat considerind ca val. medie I₂= componenta continua a lui I₂ se inchide prin sarcina (R) iar componentele alternative se inchid prin condensator .Pt. acesta facem analiza functionarii continue a convertorului :

In intervalul de conductie T_on : i_c=i_L-i₂=I_Lm+(I_LM-I_Lm) t/DT- I₂ =(I_LM-I_Lm) t/DT-(I_LM-I_Lm)/2 (5) . Pe de alta parte : ic(DT)=I_CM=(I_LM-I_Lm)/2=DI_L/2 . (6)

I₂=val. medie , I₂=(I_LM+I_Lm)/2 .

Pp. ca se ramifica numai prin R iar componentele alternative ale lui I_L se ramifica prin C aria hasurata DQ reprezinta o sarcina aditiva iar riplul tens. de OUT se pote calcula :

DU₂=DQ/C=(I_CM)*(T/2)*(1/2)*(1/C)=DI_L*T/8C (7)

In int. toff riplul de curent se pote determina :

DI_L=U₂*(1-D)*T/L=D*(1-D)*U₁*T/L (8) . Din(7)si(8) =>DU₂=T²*U₂*(1-D)/8*L*C (9) sau val normata :

DU₂/U₂=1/8*T²(1-D)/L*C=p (1-D)*[(f₀/f)²]/2 (10)

unde am notat f=1/T iar f₀=1/2p LC .

Din rel. (9) se poate spune ca riplul tens . este max pt . val . maxima a riplului curentului .Val. max. a riplului de tens. : DU_2max=U₁/(32*L*C*f²) - utila pt. ca permite dimensionarea lui C avind impuse celelalte marimi electrice . Rel. (10) arata ca riplul tens. poate fi minimizat plasind polul FTJ a.i. (f₀<<f )

De asemenea din relatia (10) se pote obs. ca avind U₂=ct. riplul tens . de OUT este independent de puterea furnizata sarcinii .De mentionat ca la sursele de alimentare cu functionare in comutatie riplul tens . de OUT se situeaza sub 1%. Din acest motiv ramin practic valabile tote relatiile care au fost scrise pt. U₂=ct. (eroarea este f. mica).

CONCLUZII (1) Conv. BUCK este simplu necesitind un singur contactor static CS . Viteza de variatie a curentului prin acest CS este lim. de val. lui L=di/dt ->panta de variatie a curentului . (2) (2.a) Regimul de scurtci 141j98b rcuit -> in int. t_on sursa de IN U₁ este direct conectata la sarcina . Din acest motiv este necesara protectia CS. (2.b) In int. t_off sursa U₁ este deconectata dar prin dioda D este eliberata energia acumulata in inductanta L. De asemenea in acest caz este necesara protectia diodei D la scurtcircuit pt. filtre . (3) (3.a) Inafara de FTJ necesar la OUT din cauza discontinuitatii curentului debitat in oricare regim de functionare de catre sursa U₁ este necesar un FTJ si la IN pt. optimizarea regimului energetic al acesteia . (3.b) In regim de functionare discontinua componenta spectrala a curentului prin inductanta creste iar din acest motiv la acest regim de functionare este necesar un filtru EMI pt. atenuarea regimului de perturbatie electromagnetica .

EOF
(F1P1C3) Continuare???????curs 4???

Curentul mediu la IN = curentul mediu prin L: I_L=I₁=U₁*D*T*(D+D₁)/2L ;

I_L=I_LM*(D+D₁)/2    (12).Din rel. (11) si (12) I₂=T*D₁*D*D₁/2L    (13)

In cazul surselor de tens. la care U2=ct. si rap.de conductie D se modifica ca raspuns la var. sursei de IN U₁ este util de a se prezenta rap. de conductie D ca o functie de raport de transfer N : D = f (U₂/U₁) .Din (13)+(10)+(7) D=[4/27 *U₂/U₁ *(U₂/U₁ -1) *I₂/I_2max] ^1/2 ;

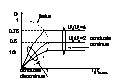In regim de conductie discontinua daca U₂ nu este controlat in timpul fiecarei perioade de comutatie , cel putin , cantitatea de energie este transferata de la IN la OUT prin condensator si sarcina . Daca sarcina nu e capabila sa absoarbe aceasta energie -> tens. pe C deci si in sarcina poate creste pina cind se stabileste echilibrul energetic ->daca rezistenta de sarcina creste scade curentul prin sarcina ; cresterea tens. U2 poate cauza distrugerea condensatorului de iesire sau aparitia unei tens. de val. mare poate produce evident avaria echipamentului alimentat.

Elemente de proiectare si performanta

a) determinarea riplului tens. de iesire

Pt. aceasta pp. functionarea convertorului in regim de conductie continua,considerand formele de unda corespunzatoare respectiv unui regim. Pp. ca riplul curentului prin dioda se inchide numai prin condens., iar componenta continua prin rezistenta de sarcina putem sa trasam urmatoarele diagrame:

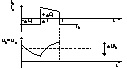In int. (0 , DT) :

i_c= -i₂ = -I₂ (15) >Riplu vf. la vf. se poate exprima ca:

DU₂=DQ/ C=I₂*D*T/C=U₂*D*T/(R*C) (16). Variatia normata a riplului :

DU₂/U₂=D*T/(R*C)=D*T/t (17) .O analiza similara se poate face si pt. celelalte regimuri liniare .

b). Efectul elementelor parazite

Elem. parazite se datoreaza pierderilor asociate in bobina L, condensator C ,contactorul static CS si dioda D .Spre deosebire de caracteristica ideala, U₂/U₁ descreste cu cit raportul de conductie se aproprie de unitate.

Din cauza utilizarii limitate a CS la val. mari pt. rap. de conductie D , rap. de transformare in aceasta regiune este limitat din pct. de vedere practic , iar in situatia cu D=1 in locca U2/U1 acesta devine 0 , deci in concluzie efectul elem. parazite devine din ce in ce mai pronuntat cu cresterea rap. de conductie D

EOF

(F1P1C4) (3.)Regimul de conductie discontinua

Ca urmare a scaderii curentului mediu prin sarcina se trece in regim de functionare discontinua .

T

u₂ dt=0 , U₁*D*T-U₂*D₁*T=0    (10) 0

U₂/U₁=D/D₁ .

Situatia surselor cu functionare in comutatie .U₂=ct.; D=f(I₂/I_2Lmax) ; din P₁=P₂ I₁/I₂=D/D₁ si I₂/I₁=D₁/D (11) I₂= (I_LM/2)*D₁ (12) I₂=(U₂*D₁*T/2L)*D₁ (13).

Tinind cont de (7) si inlocuind in (10) si (13) se obt. pt. D : D=(U₂/U₁)* I₂/I_2Lmax (14) .

In situatia U₂=ct. pt. cele 3 reg. de functionare -> caracteristicile utile pt. proiectat o sursa cu functionare in comutatie .

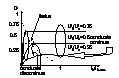Elemente de performanta si proiectare

a). riplul tens. de OUT -> pote fi determinat , spre ex. in modul continuu de functionare , in conditiile unei val. finite a cond. de iesire , pp. ca toate componentele riplului de curent se inchid prin cond. , iar val. medie a curentului se inchide prin rezistenta de sarcina . Curentul prin dioda

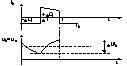DU₂=DQ/C=I₂*D*T/C (15) sau

DU₂=U₂*D*T/(R*C) (16), DU₂/U₂=D*T/t

b). efectul elem. parazite

Analog cu conv. Boost elem. parazite au un impact puternic asupra rap. de transformare si asupra stabilitatii la functionarea in bucla inchisa a conv.

Concluzii

-> variatorul boost = eficient, simplu, fiind realizat cu un singur CS la care vit. de variatie a cur. di/dt este limitata de prezenta inductanteei L .

-> in int. de acumulare a energiei in L sursa U1 = izolata de sarcina ceea ce e bine in cazul unui scurt circuit la OUT .

-> tens. de OUT =senzitivitate prea mare in rap. cu D ceea ce face ca sa apara unele probleme de stabilitate. in cazul surselor stabilizate de tens. (U2/U1=1/(1-D)).

-> curentul mediu de OUT avind o val. mai redusa decit cel de IN determina ca restul componentelor sa se inchida prin intermediul filtrului o val. mai mare pt. L si C decit la Buck.

-> circulatia continua de curent la IN = mai mare la IN ->necesare filtre FTJ la IN +circ. EMI.

Concluzii pt. convertorul BUCK BOOST :

1). Curentul I1 prin sursa este discontinuu ceea ce implica utilizarea unui FTJ la IN . De asemenea avind in vedere componenta spectrala bogata a cur. de IN este obligatorie utilizarea unui filtru de tip EMI pt. reglarea perturbatiilor de natura electromagnetica .

2). In intervalul acumularii si eliberari de energie in sarcina circ. de IN si respectiv OUT sunt izolate intre ele ceea ce ofera o buna protectie la scurtcircuit in intreg int. de functionare a variatorului .

EOF

(NEFOLOSITA-F1P1C5)

(NEFOLOSITA-F1P2C1)

(F1P2C2) EI C5 Fata

Convertorul Cuk = conv. c.c. -c.c. cu rap. de trans. oarecare N >=< 1 .

->acest conv. este obtinut primn utilizarea principiului dualitatii , similar cu conv. Buck-Boost .

->asigura la OUT o tens. medie cu pol. negativa fata de terminalul comun IN/OUT .Aici C actioneaza ca principal mijloc de inmagazinare si transfer de energie de la IN la OUT .

Sch. principala contine :

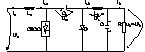U_c1=U₁+U₂ . Pp. ca C₁ de val. suficient de mare , in reg. stationar de functionare , variatia tens. U_c1 de la val. sa medie pote fi pp. neglijabila chiar daca C inmagazineaza sau cedeaza energie .Cind CS este blocat , I_L1 si I_L2 se inchid prin dioda D , C₁ este incarcat prin D cu energia de la IN si energia din L₁ < cur. I_L1 scade deoarece U_c1 >U₁ . In acest interv. energia inmagazinata in L₂ este transferata iesirii, deci curentul respectiv (I_L2) deasemenea trebuie sa scada . Cind CS in conductie ,U_c1 polarizeza invers dioda D , cei 2 cur. I_L1 si I_L2 se inchid prin CS . Deoarece U_c1>U₂ , C₁ se descarca prin contactorul static , transferind energia la OUT ; deci si lui L₂ , I_L2 creste . Deasemenea IN alimenteaza cu en. inductanta ,I_L1crescind .

In aceasta situatie avem pt. tens. si cur. prin cele 2 inductante in reg. de functionare continuu :

Pt. int. t_off sch. echivalenta :

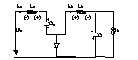
Pt. int. t_on sch. echiv. :

Sa determinam raportul de transformare :

L₁: (U₁-U_c1)*(1-D)*T+U₁*D*T=0 (1) U_c1=U₁/(1-D) (2)

L₂: -U₂*(1-D)*T+(U_c1-U₂)*D*T=0 (3) U_c1=U₂/D (4)

Deci U₂/U₁=!/(1-D) (5) .Pt. rap. curentilor : (P₁=P₂) I₁/I₂=U₂/U₁ I₂/I₁=(1-D)/D .

(I₂=I_L2 ; I₁=I_L1 ).

) si o alta metoda de a obt. expresiile de mai sus . I_L1 si I_L2 admitem ca sunt fara riplu .

i_L1=I_L1=ct. ; i_L2=I_L2 cind CS este in ON se elibereaza de catre C o cantittate de sarcina egala cu Q=I_L2*D*T .Pt. ca in regim stationar variatia de sarcina pe C sa fie nula intr-o perioada este necesar ca :

I_L1*(1-D)*T=I_L2*D*T I_L2/I_L1=(1-D)/D= I₂/I₁ si

respectiv U₂/U₁=D/(1-D) deoaorece P₁=P₂ .

Concluzii :

(1.) conv. Cuk are functionarea bazata pe transferul energiei de tip capacitiv , spre deosebire de Buck-Boost . circ. are o eficienta mai mare avind pierderi mai reduse .

(2.) un avantaj important este acela ca .... curenti de IN si OUT sunt in mod rerzonabil fara riplu spre deosebire de conv. B.-B. unde curentii sunt deiscontinui .... I_L>0 .

(3.) Un dezavantaj semnificativ = necesitatea unui C₁ cu posibilitatea unui riplu mare de curent in el .

EOF

(F1P2C3) EI CURS 4

Variator c.c.-c.c. cu raport de transformare oarecare Buck-Boost

Conventional se pot obtine pt. un anume variator situatii practice N 1.Aplicatia principala : sursele de tens. cu functionarea in comutatie . La acest tip de convertor , la OUT se obt. o tens. de polaritate negativa in raport cu respectarea terminalelor comune ientrare/iesire .Pe de alta parte , raportul tens. de OUT U₂/U₁=D/(1-D), asta in val. absoluta caci de fapt U₂/U₁<0.

In principiu un conv. Buck-Boost poate fi evident obtinut prin conecterea in cascada a doua conv. BUCK, BOOST insa este neavantajos ca conectarea sa se faca prin cascadare si rezulta solutia:

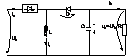Functionarea la IN in conductie a CS se acumuleaza energie in bobina de la sursa de IN . Dioda D este pol. invers in acest interval . La blocarea contactorului static tens. de autoinductie de pe L deschide D si energia inmagazinata in L se transfera circ. de sarcina .In analiza pe care o efectuam vom considera : u₂(t)=U₂=ct. , i₂(t)= I₂=ct. (C mare).

1). Regimul de conductie continua

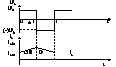In ambele situatii sarcina si sursa sunt practic izolate , ceea ce ofera practic un avantaj in ceea ce priveste regimul de scurtcircuit .

u₂ dt =0

U₁*D*T-U₂*(1-D)*T=0 N=U₂/U₁=D/(1-D) [cea ce am obtinut si prin conectarea in cascada a conv. Buck-Bost ] I₂/I₁=(1-D)/D [P₁=P₂] .

2). Regimul limita

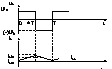Presupunind ca U₂=ct. in cazul surselor stabilizate de tens. : I_LL=I_LM/2+T*U₂*(1-D)/2L (4); I₁=DI_LL

I_2L=I_LM(1-D)/2    (5) I_2L=T*U₂*(1-D)²/2L (6).

Se poate observa ca I_LM si I_2L au valori maxime , ipotetic , pt. D=0 .

I_LLmax=I_2Lmax=T*U₂/2L    (7) pt. D=0 ; I_LL=I_LLmax*(1-D) ; I_2L=I_2Lmax*(1-D)² .

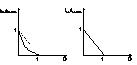
EOF

(F1P2C4) EI Cursul 3

Variator/convertor cu rap. de transformare supraunitar - BOOST (N>1)

Aplicatiile principale ale conv. Boost sunt sursele stabilizate de tens. cu functionarea in comutatie si in sist. de actionare a motoarelor de c.c.

Topologia : prezinta cele 3 elem. cheie : CS , L de acumulare si D dispusa ca in fig. :

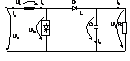Conceptul conv. Boost este de tip indirect cu functionare in clasa A (intr-un cadran) avind tens. de OUT > decit tens. de IN (ca val. medii) . Cind CS se gaseste in starea ON , D este polarizata invers aceasta determinind izolarea iesirii fata de intrare . In acest interv. intrarea asigura acumulare de energie in L . La blocarea CS-ului iesirea primeste energie din circ. de intrare reprezentat de sursa U₁ si tens. autoindusa in L (tens. are polaritatea din paranteze )!!! Pune-o tu!!! .

In analiza pe care o vom desfasura in continuare pp. u₂(t)=U₂=ct.

1.Reg. de conductie continua

Se are in vedere analiza unui regim stationar pt. care curentul prin L nu prezinta intreruperi I_L(T)>0

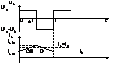In primul int. tens. U₂ este U₁ pt. ca CS e deschis -> scurt . La acest tip de convertor :

U₁-U₂<0 , U₂>U₁ , U₂,U₁>0 , i_L=i₁ . Pt. cele 2 secvente de comutare considerind elem. de circ. ideale putem avea :

Le vei desena fara CS respectiv fara dioda si tensiunile pe bobina. iar in loc de R gen ideal de curent -> !!! FIG. 5

In primul int. de timp in circ. de intrare energia este furnizata de L iar C mentine circulatia de curent in sarcina .In cel de-al doilea int. sursa de alimentare debiteaza energie in circ. de sarcina . Retrocedarea energiei stocate de L si in plus sursa U1->acest circ. poate furniza la OUT U2>U1 . Pentru regimul stationar mentionat putem scrie:

N=U₂/U₁=D/(1-D) (2)-rap. de conversie/transf.

La var. limita ale lui D N ) .Pt. elemente ideale de curent puterea furnizata de circ. de IN = put. debitata in sarcina : P₁=P₂ U₁*I₁=U₂*I₂ I₂/I₁=(1-D) (3)

Val. medie a lui I₂ < I_L= val. medie a lui I₁ .

2.Regimul de conductie limita

Ne referim la punctul de trecere/granita dintre conductia continua si cea discontinua .

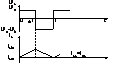I_LL=I_LM/2=U₁*DT/2L=T*U₂*D*(1-D)/2L

Acceptind ca acest variator este ridicator de tens. curentii prin L si prin sarcina sunt egali , folosind rel. (3) obt. pt. curentul prin sarcina la limita de curent :

I_2L=D*(1-D)²*T*U₂/2L (5)

Curentul max . prin inductanta L atinge val. max. pt. D=0.5 : I_LLmax=T*U₂/8L    (6)

Pt. curentul I₂L maximul se obtine pt. D=1/3 : I_2Lmax=2/27*(T*U₂/L) (7)

In functie de val. maxime ale celor 2 curenti avem : I_LL=4*D*(1-D)*I_LLmax

si I_2L=27*D*(1-D)²*I_2Lmax/4 (9)

Relatile de mai sus au fost reprezentate pt. U2=ct. situatie prezenta la sursele stabilizate de tens. iar in aceasta situatie la limita conductiei de curent considerind pe D=var. reprezentam functiile de la (8) si (9) :

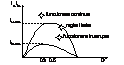
Pt. D impus avind U₂=ct. daca curentul prin sarcina scade sub I_2L avem regimul de functionare discontinua .

CURS 4

3. Regimul de conductie discontinua

Pp. ca U₁ si D sunt ct . Conductia de curent discontinuu apare datorita scaderii de curent in sarcina deci si la IN (am pp. ca P1=P2) . Intrucit I_Lm este pp. aceeasi in ambele regimuri de functionare (continua/discontinua) o val. mai mica pt. I_L in modul de functionare discontinua ( si de aici un reg. continuu cu I_L este posibil numai daca tens. de OUT creste ).

In ceea ce priveste forma de unda a curentului ea este liniara .

T

u₂dt = 0 U₁*D*T+(U₁-U₂)*D₁*T =0 (10).

N=U₂/U₁=(D+D₁)/D₁ iar I₂/I₁=D₁/(D+D₁) (11) (pt. ca P₁=P₂)

EOF

(F1P2C5) In timpul operarii cu un set de valori date : T,U₁,U₂, L si D. Daca curentul mediu prin bobina deci si cel prin sarcina devine mic decit cel furnizat de relatiile de mai sus , atunci i_L devine discontinuu .

(2.3.1)Regimul propriu-zis de functinare discontinua

Aceasta aplicatie se intalneste la motoarele de c.c. cu U₁=ct. , U₂=reglabila prin ajustarea factorului de umplere D .

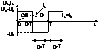
Circ. echivalent pt. ultimul interval indica o schema echivalenta in care dioda D se afla in blocare

La depasirea limitei de curent , mentinind ct. T, L, U₁ , D si scazind puterea furnizata in sarcina curentul mediu prin L scade. Aceasta dicteaza o valoare mai mare pt. U₂ rezultind astfel un curent discontinuu atit prin L cit si prin sarcina . In timpul intervalului _T tensiunea la bornele lui L devine 0. Inductanta pierzindusi rolul de distribuitor de energie intre IN si OUT . In acest regim de functionare avind U₁=ct., suntem interesati de trasarea caracteristicile externe U₂/U₁ functie de curent .

(U₁-U₂) D T-U₂ D₁ T=0 ;

U₂/U₁=D/(D+D₁) ;

In intervalul de conductie (D+D₁)<1 I_Lmax=U₂ D₁ T L ;

Val. medie a curentului prin L si D : I₂=I_Lmax D D₁ U₂ D D D₁ D₁ L (U₁ T D₁ D) L I_LLmax D D₁

D₁ I₂ I_LLmax D

Din relatiile anterioare se poate observa ca : U₂/U₁=D²/(D²+I₂/(4 I_LLmax)).Caracteristica externa a variatorului la convertorul BUCK pt. regimul de conductie discontinua avind U₁=ct. arata astfel :

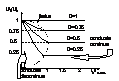
Limita - este locul geometric al tuturor punctelor de functionare ce reprezinta conductia la limita de curent.

Se continua cu conductia discontinua !!!

EOF
(F2P1C1) EI CURS 6

Topologii izolate de conversie c.c.-c.c. cu excitatie bidirectionala

- topologia PUSH-PULL ,HALF-BRIDGE si FULL-BRIDGE .

In cazul topologiilor cu un singur CS (FLYBACK sau FORWARD ) controlul este efectuat prin metodele clasice de modulatie PWM sau PFM .Topologiile cu un singur CS stau la baza topologiilor conv. cu excitatie bidirectionala .In aceste top. nr. de CS creste iar tens. de OUT se obt. de obicei prin redresarea dubla-alternanta cu punct median .

Topologia PUSH-PULL (in contratimp) :

-cuprinde 2 CS complect comandate , realizate cu disp. VMOS .

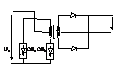
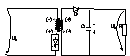t_on=timpul de comutare in conductie a unui contactor/ grup de contactoare .

D=interval de pauza .

O tens. liniar var. cu frecv. dubla fata de frecv. de lucru a circ. este intersectata cu o tens. de control .In pct. de intersectie se genereaza comanda pt. contactore .Se pune problema ... in comanda :

- grupul CS-urilor trebuie comandate simetric = cu aceeasi raport de conductie , inrucit la controlul in semipunte , daca nu sint comandate simetric , este posibil sa apara in reg. de cond. continua o incarcare a miezului magnetic , mutarea pct. de functionare pe caracteristica .... B,H a miezului ceea ce poate

provoca saturatia miezului magnetic.

- pt. a elimina comp. continua care depinde pct. de functionare pe caracteristica B,H se introduce un condensator .

Analiza conv. FLY-BACK (conv. cu revenire )

- este direct derivat din topologia de baza neizolata Buck-Boost .

Pt. starea de conductie a lui CS polaritatea tens. este +;- .In ac. sit. circ. de sarcina -izolat de primar , pt. ca D e pol. invers .In acest int. de timp este acumulata en. in miezul magnetic. La blocarea CS tensiunea este cea cu paranteze si are loc transferul en. inmagazinate in miezul mag. catre circ. de sarcina pt ca D este deschisa.Se numeste cu revenire pt ca energ. este furnizata sarcinii in starea de blocare .

Schema echivalenta a convertorului (cu inductantele de scapari care dau functionarea conv la frecv. inalte)

D=contactor necomandat

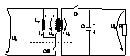Pt. frecv. joase in sch. echivalenta a trans. a fost considerata numai inductanta de magnetizare Lm . Infasurarea 2 este pur si simplu figurativa -> sa aratam ca pe acolo circula i1, curentul replica al lui i2, insa in Lm se inmagazineaza en.

Diagramele ce caracterizeaza functionarea

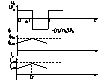(in blocare gasim in primar replica tens. U₂)

U₂/U₁=n₂/n₁.

F=variatia fluxului mag.

Toate diagramele corespund reg. de functionare continua a convertorului .

i_m=curentul de magnetizare .

Urmaeza determinarea rap. de transformare in curent continuu :

T

u₁ dt=0 U₁*D*T- U₂*(1-D)*n₁/n₂=0

N=U2/U1=(n2/n1)*[D/(1-D)].

sau U₁=n₁*dF/dt=n₁*DF DT , U₂=n₂*dF/dt=n₂*DF/[(1-D)*T] .

b). solicitarea CS pe val. max. de curent si tens. In int. t_off ->muta originea in 0

i_m(t)=I_mM-(n₁/n₂)*U₂*t/L_m , i_d=(n₁/n₂)*i_m(t) ,

(1-D)*T

id dt I_mM=(n₂/n₁)*[D/(1-D)]*I₂+(n₁/n₂)*[(1-

-D)*T/(2*L_m)]*U₂ ,

I_mM=I_CSmax .

In ceea ce priveste tens. max. pe CS : U_CSmax aceasta tens. apare in starea cind CS =blocat : U_CSmax=U₁+(n₁/n₂)*U₂=U₁*[1/(1-D)] , U₁-tens. la borne , (n₁/n₂)*U₂- tens. reflectata din secundar .Cel mai defavorabil caz : cind D U_CSmax (suprasolicitat).

EOF

(F2P1C2) EI CURS 7

Surse de tens. cu functionare in comutatie

Cerinte de proiectare :

a). iesirea sursei trebuie sa fie reglabila

b). tens. de iesire trebuie mentinuta ct. cu un anumit grad de toleranta atit la var. de sarcina cit si la var. tens. de alimentare

c). sursa este cu izolare galvanica iesirea trebuie izolata electric fata de sursa primara de alim.

d). cu iesiri multiple difera functia de putere necesitata la iesire

e). iesirile/ izolate electric intre ele

f). reducerea gabaritului sursei ; cresterea randamentului de transfer .

Iata citeva elem. care au stat la baza surselor liniare :

Schema bloc :

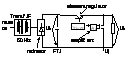
0Tens. U1 prezinta un riplu .Tiristorul regulator lucreaza in regiunea activa .

Tr. o rezistenta controlata in curent sau tens. Ot. minimizarea pierderilor pe tr. regulator este necesar ca intre tens. u1 si u2 diferentele sa fie minime atit cit sa permita ca tr. sa lucreze in RAN . UCE=U1-U2 ; daca diferenta este mare si put. debitata este mare . Cel mai defavorabil caz : in regim de scurt la OUT i2=max. -> UCE=U1.

Pt. val. mari ale curentului de OUT si tens. reduse UCE put. disipata pe elem. regulator serie este max. .

Prezenta unui transformator de JF care are dimensiunile >> decit un transf. de aceeasi putere dar care functioneaza la frecv. > .

Pierderile de putere pe tranzistorul regulator serie care functioneaza in RAN :

randamentul sursei de tip liniar =P2/P1 <50% .

In opozitie cu sursele liniare de tens. , transformarea liniara de tens. de la un nivel la altul este realizata de conv. c.c.-c.c. studiate anterior .Conv. sunt construite cu CS-uri ce functioneaza in regim ON-OFF , pierderile sunt diminuate fata de functionarea in regim activ .

Schema bloc generala pt. o sursa in comutatie :

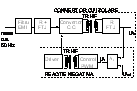
Avantaje :

1). functionarea in comutatie spre deosebire de funct. in RAN ->reducerea pierderilor cu 70% - 95% .Pt. randamente f. mari nu se utilizeaza conv. de c.c. cu modulatie in impulsuri ci fol. ZVS , ZVC(conv. c.c.-c.c. de tip rezonant )- zero voltage/curent switching .

2). utilizarea transf. de inalta frecv.

EI CURS 8 continuare la 7

Schema bloc a sursei cu funct. in comutatie :

Z_i, Z_f =impedante ; u_c=tens. de OUT din AEC (amplif. de eroare si compensare ) ;d=rap. de conductie ; u₂=tens. de OUT din conv.

Pt. modelul de sem. mic redesenam :

T₁(s)=T_m(s)*T_p(s) ,T_m, T_p-funct. de transfer ale etajelor .

Daca tens. de referinta = ct. -> perturbatia pe acest nivel de c.c. este 0.

T_m(s)= d/ u_c(s) ; T_p(s)= u₂(s)/ d(s) T₁(s)= u₂(s)/ u_c(s) .

_EOF

(F2P1C3) EI CURS 9

ControlerulPWM(modulator)- cel mai simplu este cu modulatie in durata. Consideram ca forma de unda modulata se obtine in urma intersectiei unui semnal liniar variabil cu tensiunea u_c(t).

u_c=U_c+ u_c ->ultimul termen este componenta perturbatoare

u_c=a sin(w_dt-f) ; d-raport de conductie

d(t)=|1, u_c(t)>=u_r(t)

|0, u_c(t)<u_r(t)

dezvolt in serie:

d(t)=U_c/U_r+(a/U_r)sin(w_dt-F

d(t)=D+ d ; D=U_c/U_r ; d=(a/U_r)sin(w_dt-f

Definim functia de transfer a controllerului

T_m(s)= d(s)/u_c(s)=1/U_r e constant.

Intirzierea de faza e practic nula pentru ca modulatorul are raspunsul foarte rapid fata de restul circuitului. Acest modulator este realizat cu un comparator. In practica, lucrurile stau putin diferit ;caracteristica modulatorului:

d(s)/u_c(s)=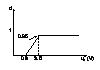

Cunoscind functia de transf. a modulatorului notam:

T₁(s)=[ u₂(s)/ d(s)] d(s)/u_c(s)]=T_p(s) T_m(s)

Amplificatorul de eroare si compensare, elemente de stabilitate

Functia de transfer pe bucla:

T_OL(s)=T₁(s) T_c(s) ;

T_c(s) functia de transfer a amplif de err si compens.

Pentru T₁ impus , T_c trebuie realizata a.i. T_OL sa indeplineasca cerintele de stabilitate ale sursei:

amplif. la frecvente joase trebuie sa fie suficient de mare pentru a minimiza eroarea stationara in tensiunea de iesire DU₂/U2->0

frecventa de taiere (frecv la care T_OL trece prin 1 sau 0db),w_c trebuie sa fie cit mai mare , cel putin cu un ordin de merime peste frecventa de comutatie f=1/T pentru ca sursa sa raspunda rapid la variatiile rezultate ca urmare a unor perturbatii in sarcina .

marginea de faza PM=F_OL F F

din conditiile de stabilitate rezulta ca valoarea absoluta a lui PM trebuie sa fie PM=45⁰..60⁰.

ideea de stabilitate pe baza diagramelor Bode consta in aceea ca 20|T_OL(jw)| sa treaca prin 0db inainte ca faza F_OL sa treaca prin (-180⁰

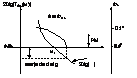
Schema amplif:

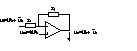
pasivizam componentele de curent continuu si rezulta functia de transfer:

u_c/ u₂=z_f/z_I=-T_c(s)

putem introduce pereche pol-zero sau zero in origine => T_c(s)=(A/s) (s+w_z)/(s+w_p) Introducerea polului in origne face ca faza lui T_c(s) sa plece de la -90⁰. Prezenta zeroului determina cresterea fazei > -90⁰ iar datorita polului faza se intoarce catre -90⁰. Parametrii in ultima relatie trebuie astfel alesi incit faza minima a functiei T_c(s) sa se produca la w_c a functiei T_OL(S).

Tehnici de control PWM

1 Control direct.

In controlul direct factorul de umplere d, dc apar var. ale tens de IN se produce o err in tens de OUT care eventual este corectata prin intermediul buclei de reglare in tensiune . Pt acest sistem de control al PWM raspunsul este lent , cu dinamica redusa la variatiile intrarii.

2 Controlul PWM cu avans de faza.

Dezavantajul de dinamica mentionat anterior poate fi minimizat dc raportul de conductie este ajustat nemijlocit functie de variatia intrarii. Aceasta se realizeaza prin modificarea la intrarea controllerului PWM a amplitudinii tens de referinta , (deci si a pantei acesteia ), care var proportional cu tensiunea de intrare.

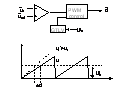
obtinem functie de transfer cu avans de faza.

EOF

(F2P1C4) Elementele de protectie a surselor cu functionare in comutatie :

In sursele realizate actual in componenta modulatorului PWM sunt prevazute o serie de circ. aditionale , ce au posibilitatea comenzii la aparitia regimului de avarie .Un circ. UC1524A si care are in el tot ceea ce necesita partea de control a unei surse cu functionare in comutatie (UNITRADE).

Circ. de protectie au rolul :

1). protejarea dispozitivelor contactorului static si ale redresorului in mom. pornirii sursei .

Aceste solicitari apar deoarece la pornire , condensatoarele de filtrare sunt initial descarcate ,comportindu-se ca un scurt .

(continuare C9)curs10

Elementele de protectie a surselor cu functionare in comutatie :-> blocul de comanda PWM sesizind initial absenta tens. de OUT tinde sa comande CS cu factor de umplere maxim desemnind in regim dur de funct pt. CS .Circ.de protectie trebuie sa determine in aceasta situatie intrarea in functionarea sursei (spre atingerea reg. stationar ) printr-o procedura lenta = soft-start , care consta in comanda CS-urilor cu factor de umplere lent crescator , pina la atingerea reg. normal de functionare .

2). protejarea sursei in cazul de scurt la OUT ->prin blocarea comenzi CS-ului .

Important : dupa activarea acestui circ. , starea iesirii este testata in mod periodic iar dupa disparitia cauzei care a generat activarea protectiei functionarea sursei este reluata automat prin procedura lenta .

3).protejarea sursei la supratens. de OUT , care poate aparea daca sarcina conectata impune un cur. redus si ca urmare ( ) posibilitatea aparitiei unui reg. intrerupt de functionare a conv. PWM .

A 2 posibilitate -> supratens. respectiva poate aparea ca urmare a deteriorarii buclei de control a tens. Cele 2 sit. pot fi eliminate . In primul caz protectia o asigura chiar bucla de reglare deoarece la val. mai mari Uc>Uref are loc blocarea comenzilor .Pt. cea de-a doua sit. este prevazut un circ. de protectie suplimentar care actioneaza la tens. de iesire U2 impusa , producind scurtcircuitarea iesirii ceeea ce det. activarea protectiei la scurt si in final blocarea comenzii .

Protectiile :

1). la curent : circ. poate fi plasat atit in primar cit si in secundar

Poate actiona cu limitarea cur. max. cit si evident la scurt .Pt. limitarea cur. se utilizeaza doua metode :

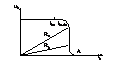La atingerea val. max. circ. mentine cur. la aceeasi val. ; toata tens. se va regasi pe elem. regulator de curent .Se obs. ca la atingerea val. limite impuse circ. de protectie actioneaza in sensul pastrarii ct. a cur. de OUT. Situatia cea mai rea -> la scurtcircuit la iesire atunci se poate realiza o alta protectie la cur. ,limitarea cu intoarcere Foldback.Motivul consta in a realiza prin sursa un cur. mai mic decit I_2L ; in acest mod are loc minimizarea regimului energetic de disipatie pt. CS-uri .

EOF

(NEFOLOSITA-F2P1C5)

(F2P2C1) PROBLEME
Aplicatie 1:

Intr-un variator Boost rap. de conductie D este reglat a.i. tens. de OUT U₂=48V , tens. de IN U₁ variaza intre 12 si 36 V .Put. max. debitata in sarcina : 120 W. Se considera ca variatorul functioneaza in regim de conductie discontinua , f=50 khz , T=1/f=20ms .

Considerind componentele ideale iar condensatorul C destul de mare a.i. u₂(t)=U₂ , sa se calculeze val. max.. pt. L a.i. sa se realizeze reg. de functionare impus .

I_2Lmax=P₂/U₂=2.5 A .

solutie:

Val. max. a inductantei trebuie determinata a.i. regimul de functionare sa ramina discontinua si in acest caz calculul se face pt. limita dintre conductia discontinua si continua . Pt. regimul de functionare corespunzator : D=(0.75 , 0.25 ) pt. acest domeniu al lui D , I_2L are val. minima pt. D=0.75 pt. L corespunzator reg. respectiv :

L_max =T*U₁*D*(1-D) ²/(2*I_2Lmax)=9mH.

Daca L=9mH , pt. U₁=12V si P₂=120W convertorul lucreaza la limita dintre regimul de conductie continua , in rest functia este discontinua->pt. asigurarea acestui regim este necesar ca inductanta utilizata L<9mH , val. care asigura regimul de granita.

Aplicatie 2:

Un conv. Buck-Boost cu functionare in regim de conductie continua are tens. de IN U₁=12V,

D=0.25, si frecv. de comutare f=25 khz , L=150mH, C=220mF, I₂=1.25A (cur. mediu prin sarcina ) . In conditiile specificate (funct. in reg. de conductie continuu) se cere :

a). tens. medie de iesire : U₂ ;

b). val. de vf. a riplului : DU₂ ;

c). val. de vf. a riplului de curent prin L : DI_L ;

d). amplitudinea curentului prin CS : I_LM ;

Solutie :

Pt. a caracteriza reg. de functionare in conditiile specificate este necesar ca I₂>I_2L .

Rel. la limita :

I_2L=T*U₂*(1-D)²/2L=T*U₁*D*(1-D)/2L=0.3 A .

I₂=1.25 A >I_2L=0.3 A -> OK ! -functioneaza in reg. continuu .

a). U₂=U₁*D/(1-D)= 4V (in realitate -4V) fata de terminalul comun IN-OUT .

b). DU₂=I₂*D/(f*C)=56.81mV .

c). DI_L=D*U₁*T/L=0.8 A .

d). curentul I₁ functie de I₂ si D se poate exprima : I₁=D*I₂/(1-D)=0.417 A .Val. vf. la vf. (din diagramele care descriu reg. de funct. continuu ) : I_LM=I₁/D +DI_L/2=2.07 A .

Aplicatie 3

Un convertor BUCK avind frecv. de comutare 25 khz cu functionare in regim de c.c. are U₁=12 V, U₂=5V iar riplul de tens. DU=20mV . Daca DI₂ este limitat la 0.8A sa se determine :

a). rap. de conductie D ; b). val. lui L ; c). val. lui C

Solutie : a). D=U₂/U₁=0.417   

b). L=U₂*(1-D)*T/DI₂ , unde T=1/f => L=146mH

c). C=DI₂*T/8*DU₂=200mF.

Aplicatie 4:

Un conv. Cuk care lucreaza in regim continuu are frecv. de comutare f=50 khz . Pt. simplitate L₁=L₂=1mH , C₁=5mF .Condensatorul de iesire C este suficient de mare a.i. sa se poata considera ca tens. de OUT este u_c=u₂=U₂=ct. ; U₁=10V iar U₂=5V puterea debitata P₁=P₂=5W . Sa se calc. erorile procentuale .... o data tens. pe C ct. si a doua oara curentii I_L1si I_L2 .

a). DI_L1/I_L1=? ; DI_L2/I_L2=? (u_c1=U_c1)

b). DU_c1/U_c1=?    (I_L1=I₁ ; I_L2=I₂=ct. )

Solutie :

a). U_c1=U₁+U₂=15V .In conditiile continue de curent : N=D/(1-D) D=0.33 .

DI_L1=(u_c1-u₁)*(1-D)*T 0.067A (u=L*di/dt) ; DI_L2=u₂*(1-D)*T/L₂=0.067 A .

I_L2=I₂=P₂/U₂=1A ; I_L1=I₁=P₁/U₁=0.5A

Erorile proc. : DI_L1/I_L1=13.4 % , DI_L2/I_L2=6.7 % .

b). Pp. ca I_L1=ct. si I_L2=ct.

(1-D)*T

DU_c1=1/C * iL₁ dt=1/C * I_L1*(1- D)*T=1.33 V .

Eroarea care se face : DU_c1/U_c1=8.87 % .

Pt. o eroare 10 % - ambele metode ramin valabile .

EOF

(F2P2C2) Convertoare CC-CA autonome

Invertoare Monofazate (invertor de tip paralel cu punct median cu alimentare in curent) Wagner

La aceasta topologie caracteristic este faptul ca condensatorul de stingere se gaseste in paralel cu sarcina , avind configuratia unui redresor cu punct median la care sa adaugat condensatorul C si respectiv sarcina. Comutatia este de tip autonom, intrarea in conductie a unuia din dispozitive atragin dupa sine blocarea celuilalt. Vom considera transformatorul de alimentare ideal cu raportul de transformare n=1. Sursa este ideala cu L . n ₃/ n ₂ = n ₃ / n ₁ = n

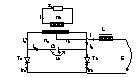
Voi desena diagramele regimului permanent de functionare:

-initial este comandat in conductie T₂

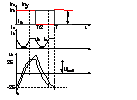
Z_S=R u=u_c/2 (datorita efectului de autoinductie ce apare la comutarea celor doua Tiristoare)

Presupunind ca la t=0, in regim stationar de functionare initial este comandat T₂ si C se gaseste incarcat din ciclul anterior cu polaritatea din figura, tensiunea la bornele condensatorului u_c=-2E.

|u_c|=2E datorita faptului ca primarul transf. lucreaza ca autotransformator ce are aplicat fata de punctul median si respectivele capete ale infasurarilor tens E, deci in total 2E. Tens la bornele sarcinii are in acel moment valoarea E. Comanda T₂ determina punerea in paralel a C pe T₁; u_AKT1 devine negativa provocind iesirea lui T₁ din conductie. Incepe descarcarea C prin intermediul transf. pe circuitul de sarcina. Pt intervalul in care are loc schimbarea polaritatii C de la -2E la 2E in circuitul respecti pot fi scrise relatiile: i₁+i₂=I ; legea solenatiei i₂n-i₁n=in ; i₁=i_c=C du_c/dt=2C du/dt ; u=u_c/2 din aceste relatii I-i=2i₁=2C du_c/dt=4C du/dt

I=i+4C du/dt=(u/R)+4Cdu/dt solutia ecuatiei este:

u=k e^-t/t+IR, t=4RC iar pentru determinarea lui K punem conditia u(0)=-u(T/2)

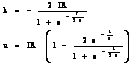
Dezavantajul unui asemenea circuit consta in posibilitatea de supracrestere a tensiunii u respectiv u_c si u_AK ce apare pe tiristorul ce urmeaza a fi blocat. Supracresterea se datoreaza acumularii de energie creativa, ceea ce inseamna ca sunt determinate conditii restrictive de functionare pt regimul de sarcina in gol. Apare pericolul strapungerii dispozitivului si la variatiile rezistentei de sarcina apar fluctuatii de majore de putere . In cazul sarcinilor complexe dezavantajul mentionat anterior se mareste in sensul cresterii si mai accentuate a tensiunii U.

Invertoare tip serie

Aceste invertoare cuprind condensatorul de stingere in serie cu sarcina formin astfel un circuit rezonant. Blocarea tiristorului ce a condus prezinta unele particularitati, nefiind necesara prezenta unui alt tiristor pentru comutare.

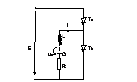
Comutatia la acest circuit se face prin sarcina si exista o conditionare pentru stingerea celu de al doilea tiristor.

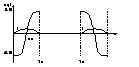
(1) L(di/dt)+Ri+u_c=| E , pentru conductia lui T₁

| 0 , pentru conductia lui T₂

(2) LC(d²u­_c/dt²)+RC(du_c/dt)+u_c= "ca mai sus"

(3) d²u_c/dt²+2a(du_c/dt)+w u_c="ca mai sus"

Aplicam transf. Laplace:

[s²U-sU(0)-U`(0)]+2a[sU-U(0)]+w U="ca mai sus

a=R/2L=atenuarea; w w a =frecv circulara ; w LC=frecv de rez proprie a circ respectiv.

Conditiile initiale:|u(0)=-KE u`(0)=0

| u(p w)=KE

Aceasta expresie se obtine la comanda T₁ iar la

EOF
(F2P2C3) 3 Control PWM cu bucla suplimentara de curent (control cu injectie de curent ). In acest mod de control este aditionata o a doua bucla de reglare .

Pentru controlul optim al unui sistem de ordinul n in cazul general trebuie utilizate n bucle de reactie independente . Rezulta ca pentru un sistem de ordinul 2 ca in acest caz avind ca variabile de stare curentul prin inductanta si tensiunea pe condensator , sunt necesare 2 bucle de reglare una in tensiune si una in curent.

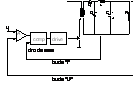
Sunt posibile trei tipuri de control prin bucla de curent. primele 2 cu frecv. ct.

CURS 11

Prima posibilitate->U_c=tens. la iesirea AEC (amplif. de eroare si compensare )

Se realizeaza compensarea U_c cu i_l depinde de D_IL, parametrii convertorului si conditiile de operare -> acest mod de c+ontrol este operational numai pt. reg. de circulatie continua a curentului .In modul discontinuu de operare curentul prin L la trecerile prin 0 ar impune o var.negativa D_IL ceea ce nu este posibil intrucit contactorul static in aceaste situatie nu mai revine in starea de blocare dupa trecerea prin 0 a curenrului I_L .

(b.) A doua posibilitate -> in situatia 2 , avind t_off=ct. , U_c dicteza val. maxima pt. I_L. La atingerea val. I_Lmax CS revine in blocare avind t_off impus prin reg. de functionare .

( c )In modul 3 , avind frecv. de comutare ct. cu comutare ON initiala , CS se deschide la inceputul fiecarei perioade T. Tens. U_c impune val. max. I_LM si respectiv momentul in care CS revine in starea de blocare ... la inceputul unei noi perioade T. Avind frecv. de lucru ct. elem. de filtrare pot fi dimensionate si proiectate in mod riguros . In practica o tens. liniar variabila este aditionata la U_c, producind un efect de control cu avans de faza si de aici imbunatatirea raspunsului sist. de reglare t_on si t_off., fiind modificate simultan , si frecv. de lucru raminind ct. Cum stau lucrurile :

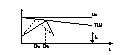
Pp. aceeasi val. medie a curentului I_L daca tens. de IN creste tens. de OUT ramine ct. prin descresterea rap. de conductie de la D₂ la D₁.Prin introducerea tens. aditionale liniar variabile se imbunatatesc de asemenea conditile de stabilitate ale sursei.

Concluzii : Modul de control cu bucla suplimentara de curent prezinta o serie de avantaje fata de modul de control PWM direct (o singura bucla de tens.).

1). Limiteaza val . max.. a curentului -> adica aceasta se face : este masura val. cur. prin CS sau prin sarcina si aceasta val. este limitata de U_cmax =val. max. care apare pt. U_c.

2). Produce deplasarea unui pol (ce corespunde filtrului de OUT) cu functia de transfer control iesire u₂(s)/ u_c(s) ceea ce poate simplifica compensarea amplificatorului in sist. cu reactie negativa , in special in prezenta in semiplanul drept a unui 0.

3). permite proiectarea modulara a surselor de c.c. care sunt conectate in paralel , impunind aceeasi val. a cur. mediu la iesirea fiecaruia (daca u_c=acelasi pt. toate sursele interconectate).

4). pt. sursele care au convertor cu functionare in PUSH-PULL elimina posibilitatea de saturare a miezului magnetic .

5). produce un mod de control cu avans de faza , rezultind un regim de lucru stabil dublat de raspunsul rapid al sursei de alimentare .

Toate metodele prezentate -> doar principial si mai ales pt. sist. analogice de reglare .Pt. sursele mai pretentioase se foloseste

Controlul digital PWM

Avantaje

1). senzitivitate mai redusa la variatile de temp., alimentare si ale componentelor.

2). cresterea fiabilitatii sursei prin reducerea consumului de putere in partea de control .De asemenea prin realizarea digitala a regulatorului PID(proportional integral derivativ) .

Realizarea PID-urilor : se pot face atit hard cit si soft , imbunatatind regimul tranzitoriu si minimizind eroarea stationara la iesire .

EOF

(F2P2C4) Liniarizarea conv. PWM si a FTJ utilizind metoda var. de stare :scopul acestei metode de mediere in spatiul var. de stare este acela de a obt. o topologie de circ. invarianta in timp .Prin sinteza se poate obtine modelul SPICE al convertorului si implicit al sursei , si care poate fi in continuare analizat d.p.d.v. al stabilitatii . Ideea acestei metode este de a obt. d.p.d.v. analitic un set unic de ecuatii liniare care sa descrie functionarea medie in reg. stationar .

T este format din T_K intervale de lucru iar T este o peroiada de lucru.Pe aceste intervale circ. isi poate schimba structura isi poate modifica structura .

n

T= Tk .

k=1

Ideea este de a obt. pe tot T un model al circ.

-> se analizeaza comportarea conv. in regim de functionare continua . Pt. fiecare ciclu de comutatie se poate scrie un ciclu de stare .

PAS 1 : X`=A₁*X+B₁*u₁ in int. dT (1). Pt. a doua secv. de comutare :

X`=A₂*X+B₂*u₁ in int. (1-d)T (2).

Matriciile A₁,A₂ - patrate , B₁,B₂ - vectori .

d.p.d.v. al iesirii u₂ : u₂=C₁*X (3) in int. d*T si u₂=C₂*X (4) in int. (1-d)*T . C₁,C₂ - vectori transpusi .

PAS 2 : redarea ec. de stare folosind rap. de conductie d ; pt. a produce modelul mediat al circ. de comutatie intr-o perioada ; in cazul nostru ec. corespunzatore celor 2 stari sunt ponderate si mediate in timp rezultind in cazul general ecuatii neliniare :

X`=[A₁*d+A₂*(1-d)]*X+[B₁*d+B₂*(1-d)]*u₁ (5)

u₂=[C₁*d+C₂*(1-d)]*X .

Nota (1) x`(t)=A₁*x(t) t (0 , t₁)

(2) aplic trans. Laplace pt. a o aduce la forma unei ec. algebrice : s*x(s)-x(0)=A1*x(s) .

(s*I-A1)*x(s)=x(0)

P[I+ (A_k*T_k)/ i!]*x(0) (I+ (A_k*T_k))*x(0)

i

sau x(t)=(I+ (d_k*A_k*T)*x(0) (12) ;

k=1

x(T) e^(A*T)*x(0) , unde A= (d_k*A_k) .

In particular pt. un curent cu 2 stari matricea mediata este :

A=d₁*A₁+d₂*A₂

B=d₁*B₁+d₂*B₂ .

PAS 3 : Sunt introduse perturbatiile de sem. mic si in continuare sunt separate componentele de sem. mic si de c.c.

x=X+ x (7), x - comp. de c.a. , X - comp. de c.c.

u₂=U₂+ u₂ (8) , d=D+ d (9) ,

u₁=U₁ pt. ca u₁=0 . (10)

Inlocuind in (5)

x`+X`=AX+BU₁+A* x+[(A₁-A₂)*X+(B₁-B₂)*U₁] d+ ... (11)

termeni care contin prod. de x si d si care sunt neglijati .

A=A₁*D+A₂*(1-D) (12)

B=B₁*D+B₂*(1-D) (13).

Regimul de sem. mare , de c.c. poate fi obtinut :

X`=A*X+BU₁ (14)

X`=A* X+[(A₁-A₂)*X+(B₁-B₂)*U₁]* d (15).

In mod similar utilizind ec. (7)->(10) si introducind in (6) :

U₂+ u₂=C*X+C* x+[(C₁-C₂)*X]* d (16) , unde C=C₁*D+C₂*(1-D) (17) ; pt. reg. continuu : U₂=C*X (18) ; pt. reg. pulsatoriu : u₂=C* x+[(C₁-C₂)*X]* d (19) ; din reg. stationar de c.c. (14)->(18) : U₂/U₁= -C*B/A (20) .

PAS 4: transf. ec. de stare din domeniul timp (t) in (s) . Se realizeaza determinarea functiilor de .... control iesire ; rel. (15)->(19) contin perturbatiile de semnal mic / componente alternative ; aplicind tr. Laplace rel. (15)

s x(s)=A x(s)+[(A₁-A₂)*X+(B₁-B₂)*U₁] d(s) (21)

x(s)=(s*T-A)^-1[(A₁-A₂)*X+(B₁-B₂)*U₁]* d(s) (22) Din rel. (19) si (22) functia de transfer control iesire notata T_p(s) : T_p(s)= u₂(s)/ d(s)=[C/(s*I-A)]*[(A₁-A₂)*X+(B₁-B₂)*U₁]+(C₁-C₂)*X    (23) .

La pasul 2 se obtine o singura topologie de circ. descrisa de ec. matriciale dar ecuatia este neliniara. ajungem la o singura ecuatie (dupa neglijarile respective) care este liniara.

EOF

(F2P2C5) Conv. FORWARD (a.) direct (ideal) = derivat din conv. de tip Buck ; se numeste conv. direct deoarece energ este transferata direct in secundarul transformatorului si in sarcina in interv. de conductie a CS-ului t_on .

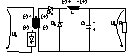=numit si "conv. ideal " .

Spre deosebire de conv. prezentate anterior ,aici transformatorul nu are un rol propriu-zis de acumulator de energie ,respectivul rol fiind preluat de inductanta L din secundarul transf. .

In t_on D₁ conduce ,D₂ blocata se transfera energ. din primar in inductanta L : U₂=(n₂/n₁)*U₁-U₂

In t_off (-) ; (+) ->D₁ blocata, D₂ se deschide -> se poate transfera energie din L in circ. de sarcina .

Pt. determinarea rap. de transformare :

T

u2 dt =0 , [(n₂/n₁)*U₁-U₂]*D*T-(1-D)*T*U₂=0 N=U₂/U₁=(n₂/n₁)*D - rel.

valabila pt. reg. de functionare continua .In conditii practice la functionarea in reg. continuu exista posibilitatea magnetizarii miezului magnetic ->trebuie gasita solutia pt. care indiferent de reg. de functionare in reg. stationar nu are loc excitatia in curent continuu a miezului magnetic .

Astfel acumularea de en. magnetica ar provoca distrugerea convertorului prin cresterea tens. aplicate CS-ului si de asemenea ar fi practic imposibila intr-o bucla de reglare ,controlul tens. de iesire .

b). convertorul real :energ. suplimentara acumulata trebuie retrocedata partial sursei de alimentare . Aceasta se poate obtine spre ex.. prin introducerea celei de-a 3 infasurari capabile sa inmagazineze si sa retrocedeze surplusul de energie .

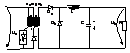In t_on se transfera en. din primar in secundar .Ceea ce se modifica ->se da comanda de blocare ->polaritatea tens. se schimba ->ne gasim in sit. in care D=deschisa ->surplusul de en. se duce catre sursa de alimentare prin D si bobina .D=dioda de recuperare in timpul t_m =timpul de retrocedare a surplusului de en. Se vede ca in tm i_m scade la 0 ; mai departe avem un int. mort , mai putin cur. care circula prin L -> reg. este unul cu circulatie continua a curentului prin circ. de conversie .

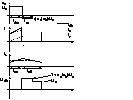
Tens. la bornele CS are 2 nivele .In regiunea in care este activa u3 -> Ucs=U₁*(1+n₁/n₃)(tens. reflectata in n₃) .In int. mort al lui n₃ ->U_cs=U₁ .

In starea t_on functia decurge ca la conv. FORWARD .La blocarea CS ,in int. de timp t_m ca urmare a intrarii in conductie a diodei de recuperare D ,este retrocedat surplusul de energie ce nu a fost disipat in sarcina (secundar) catre sursa de alimentare U1.Are loc anularea curentului de magnetizare la sfirsitul acestui moment .

Conv. FORWARD cu dioda de recuperare .

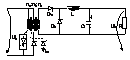0<t<ton ,u₁=U₁, cur. de magnetizare I_m in t_on creste de la 0 la Imm .La comanda in blocare :

"OFF" i₁= -i_m ; din n₁*i₁+n₃*i₃=n₂*i₂ si i₂=0

i₃= -(n₁/n₃)*i₁=(n₁/n₃)i_m

In ceea ce priveste tens. pt. infasurarea de reactie : t_m<t<(t_on+t_m) , u₁= -(n₁/n₃)*U₁ .

Demagnetizarea conduce la anularea lui I_m ,resp. la anularea tens. pe infasurarea primara .Int. de magnetizare t_m poate fi determinat luind in consideratie integrala tens. u₁ care trebuie sa se anuleze in decursul unei perioade de lucru a conv.

U₁*t_on - (n₁/n₃)*U₁*t_m =0 , t_m/T=(n₃/n₁)*D , t_m=D*T Daca se considera ca miezul este demagnetizat in reg. stationar la inceputul unui nou ciclu de conversie ,atunci penultima relatie se poate scrie :

(T - D_max*T)/T=(n₃/n₁)*D_max .

D_max=1/(1+n₃/n₁) functionarea trebuie asigurata a.i. miezul sa nu fie in sit. de a-si modifica PSF-ul la val. ale lui D D_max ->acest t_m sa se termine inainte de T .Pt. n₃=n₁ D_max=1/2.

OBSERVATII : (1)- intrucit intre primar si infasurarea secundara de reactie nu se impune un grad inalt de izolatie , cele 2 infasurari se pot realiza bifilar .Deasemenea diametrul infasurarii n3 este mic intrucit curentul de magnetizare este redus . (2) - infasurarea de reactie nu modifica expresia raportului de transformare ca in sit. in care conv. este realizat fara dioda de recuperare / infasurare dereactie secundara : U₂/U₁=(n₂/n₁)*D . (3) - tens. max. pe CS : U_csmax=U₁+(n₁/n₃)*U₁ .

- in locul infasurarii n₃, pt. anularea curentului de magnerizare ,se poate introduce o dioda Zenner care sa asigure demagnetizarea miezului in int. de blocare a CS in locul CS-ului. (4) - dimensionarea miezului : reducerea gabaritului transformatorului ; reducerea pierderilor in reg. de comutatie ; dimensionarea componentelor de EOF

FOAIA ASTA ESTE GOALA