Sistemul de parametri diferentiali ai tranzistorului bipolar

Sistemul de parametri diferentiali ai tranzistorului bipolar

Tranzistorul ca cuadripol activ

Variatiile mici ale tensiunii pe jonctiunile tranzistorului aduc la schimbari liniare în valoarea curentilor si tranzistorul devine cuadripol liniar activ. Cuadripol activ este numit circuitul electric format din elemente pasive (R, C, L) si generatoare echivalente de tensiune electromotoare sau curent, ce poseda doua perechi de borne 616f59g (fig.1.13). Perechii de borne de intrare îi corespunde curentul si tensiunea . Perechii de borne de iesire îi corespunde curentul si tensiunea .

Fig.1.13. Reprezentarea tranzistorului ca cuadripol

Sub curenti si tensiuni se subânteleg dependente de tipul

; ; (1.25)

; . (1.26)

Exista sase sisteme posibile de ecuatii pentru descrierea tranzistorului bipolar ca cuadripol, care sunt prezentate în tab.1.2.

Tabelul 1.2

Sisteme de ecuatii pentru descrierea tranzistorului

Cele mai întrebuintate în practica sunt trei sisteme de parametri si anume: Z, Y, H

; (1.27)

; (1.28)

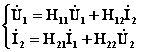. (1.29)

Parametrii diferentiali (Z, Y, H) sunt determinati din conditiile mers în gol sau scurtcircuit dupa curent alternativ în dependenta de sistemul de parametri. Rezistenta jonctiunii emitorului polarizata direct este mica si pentru obtinerea starii de mers în gol, la intrarea tranzistorului în circuitul bazei se conecteaza un rezistor cu rezistenta înalta. De aceea sistemul de parametri H este cel mai comod pentru masurari. Între sistemele de parametri Z si H exista o interdependenta. Transferul de la un sistem la altul este usor de efectuat conform relatiilor din tab.1.3.

Valorile numerice ale parametrilor diferentiali ai tranzistorului ca cuadripol depind de schema de conectare. De aceea parametrii diferentiali se noteaza cu indici suplimentari: b - parametrii tranzistorului în cuplaj BC; e - parametrii tranzistorului în cuplaj EC;c - parametrii tranzistorului în cuplaj CC.

Tabelul 1.3

Legatura dintre parametrii Z,Y,H

În tab.1.4. sunt prezentate relatiile de baza pentru parametrii H la conectarea tranzistorului EC si BC.

Tabelul 1.4

Parametrii H pentru diferite scheme de conectare

Tabelul 1.4 (continuare)

La frecvente joase, când tranzistorul nu introduce defazaj între curent si tensiune, parametrii H complexi sunt substituiti cu valori reale

. (1.30)

Sistemul de ecuatii (1.30) poate fi scris sub forma:

. (1.31)

Pentru determinarea parametrilor si la iesirea cuadripolului asiguram regim scurtcircuit dupa curent alternativ ( sau ) si, utilizând relatia (1.30) sau (1.31), obtinem:

; (1.32)

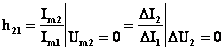. (1.33)

Pentru determinarea parametrilor si la intrarea cuadripolului asiguram regim mers în gol dupa curent alternativ ( sau ) si, utilizând relatia (1.30) sau (1.31), obtinem:

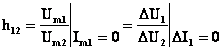; (1.34)

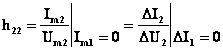. (1.35)

Coeficientii si exprimati în asa mod, au urmatoarele denumiri si unitati de masura:

- coeficient de reactie inversa dupa tensiune, când la intrarea tranzistorului este asigurat regim mers în gol;

- conductibilitatea de iesire pentru regim mers în gol la intrarea cuadripolului .

Avantajele sistemului de parametri h se explica prin comoditatea determinarii lor experimental si întrebuintarea pe larg pentru proiectarea diverselor rezolvari tehnice ce utilizeaza tranzistoare bipolare. Acest sistem permite prin masurarea nemijlocita sa determinam cel mai important parametru al tranzistorului - coeficientul de amplificare dupa curent.

1.5.2. Schemele formale pentru substituirea tranzistorului

Descrierea proprietatilor tranzistorului pentru semnale alternative cu amplitudini reduse cu ajutorul ecuatiilor cuadripolului nu este comoda la calculul schemelor practice. Pentru simplificarea calculelor se introduc schemele echivalente formale. Fiecarui sistem de parametri îi corespunde o schema echivalenta.

Pentru sistemul de parametri Z, putem scrie

(1.36)

Tensiunea de intrare prezinta suma caderilor de tensiune pe impedanta la circulatia curentului si tensiunii generatorului cu impedanta diferita de zero , care indica reactia inversa în tranzistor, adica influenta curentului de iesire asupra circuitului de intrare (fig.1.14).

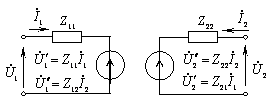
Fig.1.14. Schema formala de substituire a tranzistorului

în sistemul de parametri Z

Tensiunea la iesire este determinata de tensiunea generatorului care arata proprietatile de amplificare ale tranzistorului si caderii de tensiune pe impedanta de iesire a tranzistorului . Subliniem ca impedanta generatorului cu tensiunea pentru curentul este egala cu zero.

Pentru sistemul de parametri Y, putem scrie

.

Curentul de intrare este format din curentul ce circula prin admitanta si curentul generatorului , care determina reactia inversa în tranzistor (fig.1.15). Curentul de iesire este format din curentul generatorului ce caracterizeaza proprietatile de amplificare ale tranzistorului si curentul , care circula prin admitanta de iesire.

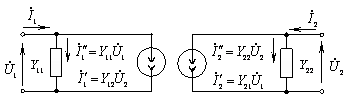
Fig.1.15. Schema formala de substituire a tranzistorului

în sistemul de parametri Y

Pentru sistemul de parametrii H sau h putem scrie

Tensiunea de intrare prezinta suma caderilor de tensiune pe impedanta de intrare si tensiunea generatorului , care caracterizeaza reactia inversa în tranzistorul bipolar (fig. 1.16).

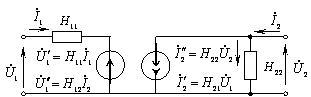
Fig.1.16. Schema formala de substituire a tranzistorului

în sistemul de parametri H

Curentul de iesire prezinta suma curentilor ce caracterizeaza proprietatile de amplificare ale tranzistorului si curentul care circula prin admitanta de iesire .

Subliniem ca admitanta nu este egala cu admitanta , deoarece este determinat în conditii de mers în gol la intrarea cuadripolului, iar - în regim de scurtcircuit la intrarea cuadripolului.

1.5.3. Determinarea parametrilor diferentiali ai

tranzistorului dupa caracteristicile statice

Parametrii diferentiali sunt determinati pentru punctul de functionare stabilit initial cu utilizarea familiilor de caracteristici statice de intrare si iesire ale tranzistorului bipolar. Pentru aceasta se foloseste metoda grafica.

În fig.1.17 si fig.1.18 este aratata metoda grafica care permite

determinarea parametrilor ai tranzistorului bipolar în punctul de functionare definit O.

Pentru schema EC relatia (1.30) poate fi scrisa sub forma

(1.37)

Pentru amplitudinile tensiunilor si curentilor, conform relatiilor (1.25), (1.26), putem scrie:

(1.38)

Fig.1.17. Determinarea parametrilor si dupa caracteristicile de iesire

Substituind amplitudinile mici ale curentilor si tensiunilor pentru semnalele variabile cu devieri finite obtinem

; ;

; ;

;

;

;

.

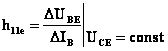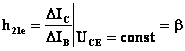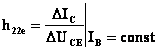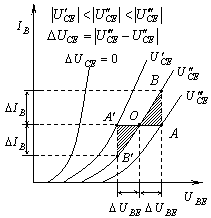
Fig.1.18. Determinarea parametrilor si dupa caracteristicile de intrare

În fig.1.17, lânga punctul O sunt construite doua triunghiuri mici OAB si OA'B' cu valori echivalente pentru , ipotenuza carora o prezinta caracteristica pentru curentul continuu al bazei . Din fiecare triunghi determinam conductibilitatea de iesire ce corespunde curentului bazei

Apoi determinam media aritmetica a acestui parametru. Din punctul dat O se traseaza o linie verticala pâna la intersectia cu caracteristica de sus în punctul D si cu cea de jos - în punctul D'. Pentru fiecare segment (OD si OD') se determina parametrul

; .

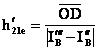Apoi calculam media aritmetica pentru parametrul dat

.

Parametrii si se determina dupa caracteristicile de intrare ale tranzistorului (fig.1.18). Pe grafic determinam punctul dat O ce corespunde marimilor si asemanator cu cel din desenul cu caracteristicile de iesire. În apropierea punctului O se construiesc doua triunghiuri mici OAB si OA'B'. Apoi din fiecare triunghi gasim parametrii si calculam media lor aritmetica. De exemplu, pentru coeficientul de reactie inversa

; ; .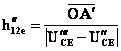