Structura discontinua a substantei si a radiatiei electromagnetice
6.1 Structura discontinua a substantei. Proprietatile atomilor
Imagini generale, de o forma rudimentara, cu privire la structura discontinua a substantei au avut deja, in urma cu 2500 de ani, invatatii Greciei antice. Astfel, in secolul 5 i.e.n., Leucip (480-420 i.e.n.) si elevul sau Democrit (460-370 i.e.n.) au format scoala greaca a atomismului, conform careia toate obiectele materiale sunt formate din particule mici, indivizibile. Democrit a introdus notiunea de atom, care deriva din cuvintele grecesti "a", ="ne" si "temnium"="a taia, a diviza". In conceptia atomistilor antici atomii reprezintau "caramizile" fundamentale ale materiei, fiind indivizibili, impenetrabili si eterni, iar din combinarea unui numar finit de atomi rezulta diversitatea lumii materiale.
Filozoful si poetul roman Titus Lucretius Carus (99-55 i.e.n.) a fost un reprezentant al atomismului antic, enumerand in lucrarea sa "De rerum natura" argumente in favoarea existentei atomilor, precum si unele proprietati atribuite acestora. El a incercat chiar sa dea o explicatie magnetismului, considerandu-l ca fiind produs prin inlocuirea vidului creat de emisia permanenta de atomi a magnetului. Lipsa unor baze experimentale si discordantele cu conceptiile lui Aristotel au condus la faptul ca multa vreme atomismul a fost considerat drept speculatie. Abia in secolul al XVI-lea se revine lent, dar sigur, catre o conceptie atomista, insa pornind nu numai de la ipoteze, ci pe baze solide, experimentale.
Ideile despre existenta inevitabila a atomilor iau nastere cand incercam sa interpretam regulile simple privind bilantul cantitativ al maselor substantelor participante la o reactie chimica, si a celor rezultate din reactia respectiva.
Dupa multe cercetari s-a ajuns la stabilirea certa ca in orice reactie chimica masa totala ramane neschimbata, adica suma maselor substantelor care intra intr-o reactie este egala cu masa substantei rezultate din noua reactie.
O alta concluzie de importanta hotaratoare
a fost constatarea ca substantele se combina numai in proportii masice
determinate, simple. Aceasta inseamna ca o anumita masa 
dintr-o substanta
poate intra in reactie chimica numai cu o anumita masa 
dintr-o a doua substanta,
iar raportul 
este independent de conditiile externe, cum ar fi proportia in
care cele doua substante au fost initial amestecate. Aceste constatari sunt
exprimate in chimie de legea proportiilor
definite (Proust, 1799) si de legea
proportiilor multiple (Dalton, 1808). Putem ilustra legea proportiilor
definite prin faptul ca 1g de hidrogen se combina cu 8g de oxigen pentru a
forma 9g de apa.
Pe baza combinatiilor azotului cu oxigenul se poate ilustra legea proportiilor multiple. Astfel, s-a constatat ca 7g de azot se pot combina cu:
1 x 4 g de oxigen pentru a forma 11 g de protoxid de azot;
2 x 4 g de oxigen pentru a forma 15 g de oxid de azot;
3 x 4 g de oxigen pentru a forma 19 g de trioxid de azot;
4 x 4 g de oxigen pentru a forma 23 g de bioxid de azot;
5 x 4 g de oxigen pentru a forma 27 g de pentoxid de azot.
Fizicianul si chimistul fancez Joseph Louis Gay-Lussac (1779-1850) a aratat in anul 1808 ca in cazul gazelor exista legi simple nu numai pentru masele substantelor ce intra intr-o reactie chimica, ci si pentru volumul lor. Astfel, la presiune constanta, doua volume de hidrogen se combina cu un volum de oxigen pentru a forma doua volume de vapori de apa.
Interpretarea acestor constatari a fost data de fizicianul si matematicianul italian Amedeo Avogadro (1776-1856), care a facut urmatoarele afirmatii:
- "fiecare gaz este format dintr-un numar mare de particule - atomii sau moleculele lui;"
- "la aceeasi temperatura si presiune, volume egale de gaze diferite contin acelasi numar de molecule."
Aceasta lege enuntata de Avogadro are o insemnatate deosebita pentru intelegerea principiilor care stau la baza realizarii diferitelor reactii chimice. Astfel, in anul 1811 Avogadro considera faptul ca doua volume de hidrogen se combina cu un volum de oxigen pentru a forma doua volume de vapori de apa echivalent cu a afirma ca doua molecule de hidrogen se combina cu o molecula de oxigen, formand doua molecule de apa. Aceasta afirmatie se exprima in zilele noastre prin cunoscuta formula chimica:
Combinarea, in unitati de masa, a unei parti de hidrogen cu opt parti de oxigen pentru a forma noua parti de apa (in unitati de masa), inseamna ca masa unei molecule de oxigen trebuie sa fie de opt ori mai mare decat masa a doua molecule de hidrogen, iar doua molecule de apa trebuie sa aiba o masa de noua ori mai mare decat masa a doua molecule de hidrogen. Vedem astfel cum chimia nu numai ca a jucat un rol hotarator in fundamentarea stiintifica a atomismului, dar ne conduce si la notiunile de masa moleculara, si respectiv masa atomica.
Deoarece masa atomilor, respectiv a
moleculelor este foarte mica, aceasta nu se masoara in grame sau kilograme, ci in
unitati atomice de masa (atomic mass unity - amu, in limba engleza). S-a
convenit ca unitatea atomica de masa sa fie aleasa astfel incat atomul 
sa aiba masa egala cu
12 amu.
Numarul unitatilor atomice de masa
care constituie masa unui atom sau a unei molecule se noteaza cu 
pentru atom si cu 
pentru molecula, fiind
denumit numar de masa. De obicei insa
se utilizeaza aceeasi notatie, de exemplu , fie ca este vorba de atom, fie de molecula. O cantitate de
substanta de masa 
grame) se numeste molecula-gram, sau mol. Daca masa substantei este 
, aceasta reprezinta un kilomol
(kmol).
La a 14-a conferinta internationala de Masuri si Greutati din anul 1971 a fost introdus in randul unitatilor fundamentale in S.I. molul, ca unitate de cantitate de substanta. Prin rezolutia a treia a acestei conferinte se specifica:
1. Molul este cantitatea de substanta
a unui sistem care contine atatea entitati elementare cati atomi sunt in 0,012
kilograme de izotop de carbon . Masa de 0,012 kg carbon 
contine un numar de atomi egal cu numarul lui Avogadro 
.
2. De cate ori se intrebuinteaza molul trebuie specificate entitatile elementare, care pot fi constituite din atomi, molecule, ioni, alte particule sau grupuri specificate de asemenea particule.
Trecerea de la unitatile de masa uzuale la unitatile ce reprezinta cantitatea de substanta (mol sau kmol) constituie un pas inainte foarte important, deoarece un mol sau kmol de orice substanta contine acelasi numar de molecule, egal cu numarul lui Avogadro. Pentru a nu se repeta excesiv cuvintele atomi sau molecule, convenim ca atomii sa fie considerati molecule monoatomice.
Daca 
este masa unei
molecule, este evidenta relatia:
, (6.1)
de unde
(6.2)
Astfel, cunoscand masa moleculara
μ pentru o substanta oarecare, putem calcula masa moleculei respective.
Pentru atomul de carbon 
numarul de masa este 
, in comsecinta 
. Astfel, unitatea atomica de masa este:
Pentru o molecula de apa (H2O) 
, deci masa unei molecule de apa este:
sau 
.
Cunoscand densitatea
unor substante se pot evalua dimensiunile atomilor sau moleculelor. Cunoscand
de exemplu ca densitatea diamantului este 
, putem evalua dimensiunile atomilor de carbon. Pentru
aceasta, admitem ca atomii au forma unei sfere de raza 
, care se aseaza in varfurile unui cub de muchie 
, formand astfel reteaua cristalina a diamantului. Volumul
unui kmol de diamant este:
, (6.3)
de unde
(6.4)
Desi aceste calcule nu sunt riguroase, configuratia atomilor in cristalul de diamant fiind diferita de cea descrisa de noi, rezultatul (6.4) este apropiat de cel adevarat. Asadar, dimensiunile atomilor si moleculelor sunt de ordinul de marime a unui Ångstrom (1Å =10-10 m).
Din legea lui Avogadro rezulta si ca
un mol de orice gaz, la o anumita presiune 
si o anumita
temperatura 
, ocupa intotdeauna acelasi volum. In conditii normale de
presiune si temperatura 
si 
un kmol de orice gaz ideal ocupa volumul 
.
6.2 Structura discontinua a sarcinii electrice
Cunoscutul fizician englez James Clark Maxwell (1831-1879) a emis in tratatul sau de electricitate si magnetism, sub forma de ipoteza, ideea existentei unei sarcini electrice elementare. Fizicianul german Wilhelm E. Weber a afirmat in anul 1871 ca in interiorul atomului exista doua feluri de particule incarcate cu sarcina electrica, avand aceeasi valoare dar de semne diferite.
6.2.1 Electroliza
Analizand legile electrolizei,
fizicianul irlandez George Johnston Stoney (1826-1911) a introdus in anul 1890
denumirea de electron pentru purtatorul
sarcinii electrice elementare negative, si a calculat valoarea acestei sarcini
electrice elementare. Vom reaminti
in ce consta electroliza, si legile acestui fenomen. In acest scop consideram o
solutie de AgNO3 aflata intre doi electrozi: cel pozitiv
-anodul - este format dintr-o placa de argint, iar electrodul negativ - catodul
- consta dintr-o placa de cupru (fig.
4.1.). In solutie are loc disocierea AgNO3 in ionii 
si 
, iar sub actiunea campului electric aplicat intre catod si
anod, ionii se deplaseaza spre
catod, in timp ce ionii se indreapta spre
anod.
Daca in intervalul de timp 
prin circuitul indicat
trece un curent electric, pe catod se depune masa 
de argint metalic, iar
masa anodului se micsoreaza cu aceeasi valoare . Aceasta nu conduce insa la variatia concentratiei solutiei,
deoarece cand ionul atinge catodul, el capteaza
un electron, transformandu-se in atom neutru care se depune pe catod, iar din
anod un atom de Ag se transforma in ionul si un electron. Ionul de
format din anod intra in
solutie inlocuind ionul depus pe catod, in timp ce electronul contribuie la mentinerea
curentului electric in circuitul exterior.
Fenomenul de electroliza este guvernat de doua legi, descoperite in anul 1833 de catre fizicianul si chimistul englez Michael Faraday (1791-1867).
Prima lege afirma ca masa depusa pe electrod
depinde de sarcina electrica 
ce trece prin circuit:
, (6.5)
unde 
este echivalentul electrochimic al substantei,
cu semnificatia fizica de masa depusa pe electrod cand prin circuit trece
sarcina electrica egala cu unitatea, si unitatea de masura in SI 
.
A doua lege indica faptul ca echivalentul electrochimic al substantei este proportional cu echivalentul sau chimic.
(6.6)
Echivalentul
chimic 
este raportul dintre
masa atomica relativa (numarul de masa) si valenta 
a ionului respectiv. O
cantitate de substanta egala cu grame reprezinta un
atom-gram din elementul respectiv.
Experimental s-a stabilit ca sarcina
electrica a oricarui ion este un numar intreg de sarcini electronice. Valenta este raportul dintre
valorile absolute ale sarcinii electrice ale ionului si respectiv sarcina
electrica a electronului.
Din (6.5) si (6.6) rezulta:
, (6.7)
unde
este intensitatea
curentului electric prin circuit. Marimea 
este un coeficient de
proportionalitate, denumit numarul lui Faraday. Valoarea acestui numar poate fi
determinata experimental. Din (6.6) obtinem:
(6.8)
Pentru argint 
iar valenta 
. Introducand aceste date in (6.8), obtinem:
Asadar,
daca prin circuit trece o sarcina electrica egala cu 96500 C, pe electrod se
depune un atom-gram din elementul respectiv. Acest lucru rezulta din (6.7), de
unde se observa ca daca 
, atunci:
(6.9)
Deoarece
valenta argintului este , din (6.7) obtinem:
(6.10)
Cu aceasta formula se
poate calcula sarcina electrica a electronului 
, cunoscand numarul lui Avogadro. In cazul cand sarcina
electrica a electronului se determina prin alte metode, din (6.10) putem
determina pe 
.
Considerand 
, obtinem:
(6.11)
Acest rationament a fost facut de catre Stoney, cu singura deosebire ca pe timpul sau numarul lui Avogadro nu era cunoscut cu precizia de azi.
S-a pus problema daca acest rationament
este intr-adevar corect, adica s-ar putea fundamenta existenta unei sarcini
electrice elementare pe baza analizei fenomenului electrolizei? A existat si parerea
ca valoarea (6.11) nu ar fi o sarcina electrica elementara, ci o valoare medie
a sarcinii electrice pentru cei ioni, a caror masa
este 
.
6.2.2 Experientele lui Millikan
Existenta indiscutabila a
sarcinii electrice elementare, si de aici a structurii discontinue a sarcinii
electrice, a fost demonstrata experimental in anul 1910 de fizicianul american
Robert Andrews Millikan (1868-1953).
Instalatia experimentala utilizata de
catre Millikan era formata din doua placi de alama si 
cu diametrul de
aproximativ 22 cm, separate intre ele printr-o distanta de 1,5 cm, si introduse
intr-o cutie metalica pentru inlaturarea curentilor atmosferici (fig.2). Picaturile
de ulei pulverizat patrund intre placile A
si B printr-o mica deschidere C practicata in placa A. Iluminand spatiul dintre placi cu
lumina de la sursa S, care este
transformata intr-un fascicul paralel cu ajutorul lentilei convergente L, picaturile pot fi urmarite prin
intermediul unui microscop.
Daca placile nu sunt conectate la o
diferenta de potential, atunci asupra picaturii de ulei actioneaza forta de
greutate a acesteia 
, careia i se opune forta de viscozitate a mediului dintre placi.
Forta datorata viscozitatii mediului fiind proportionala cu viteza particulei, echilibrul
celor doua forte se realizeaza pentru o anume viteza 
:
, (6.12)
unde 
este un coeficient de
proportionalitate. Pentru picaturile de ulei de dimensiuni foarte mici viteza
de echilibru se realizeaza rapid,
dupa ce picatura patrunde prin deschiderea C.
Conectand placile la o diferenta de potential 
viteza picaturii
variaza, deoarece prin pulverizare aceasta se incarca cu o sarcina electrica q. Forta electrica ce actioneaza asupra picaturii
este:
, (6.13)
unde d este distanta dintre placi.
In cazul in care
sarcina electrica q este pozitiva,
forta electrica 
este orientata in sus,
astfel ca noua viteza de echilibru 
se obtine din relatia:
(6.14)
In experientele
efectuate de Millikan aerul dintre placile condensatorului s-a ionizat cu
diferite tipuri de agenti, ca de exemplu raze 
sau surse din substante
radioactive. Din acest motiv, din timp in timp picatura de ulei capta din aer
un ion suplimentar de sarcina electrica, fie pozitiva fie negativa, astfel ca
viteza picaturii in campul electric dintre placi se schimba. Este posibil de
asemenea ca picatura de ulei, trecand prin aerul ionizat, sa piarda ioni. Daca
dupa un interval de timp se constata o viteza de echilibru 
, atunci considerand sarcina electrica suplimentara a picaturii
de ulei egala cu 
, se obtine:
(6.15)
Din (6.14) si (6.15) se obtine:
(6.16)
Scopul experientei era determinarea
sarcinii electrice a ionului captat sau
pierdut de picatura de ulei. Fiecare picatura de ulei era urmarita timp de cateva
ore, iar viteza se determina masurand intervalele de timp in care aceasta
parcurgea o distanta oarecare. Diferenta de potential era de mii de volti. Pentru
a calcula sarcina electrica din (6.16) trebuia
cunoscuta constanta de proportionalitate din formula lui Stokes
pentru forta de viscozitate 
.
, (6.17)
unde 
este coeficientul de viscozitate
a aerului dintre placile condensatorului, iar 
este raza picaturii de
ulei, considerata sferica. Au fost efectuate o serie de experiente pentru
verificarea valabilitatii formulei lui Stokes (6.17) in cazul unor picaturi de
raze foarte mici. S-a ajuns
la concluzia ca pentru aceste cazuri formula (6.17) trebuie scrisa sub forma:
, (6.18)
unde este presiunea aerului
in centimetri coloana mercur, iar b o
constanta ce se determina experimental.
Dintr-un numar mare de date
experimentale a rezultat ca oricare din sarcinile electrice obtinute pot fi
exprimate prin relatia:
, (6.19)
unde 
este un numar intreg,
iar este sarcina electrica
a electronului.
Ne intereseaza in primul rand
rezultatul de principiu exprimat de relatia (6.19), si nu neaparat valorile
numerice obtinute, deoarece pe timpul lui Millikan coeficientul de viscozitate nu era determinat cu o
precizie corespunzatoare. Experientele efectuate de catre Millikan au fost
repetate de multe ori de atunci, luandu-se masuri de asigurare a preciziei
necesare pentru toti parametri ce intervin in calcule. Aceste experiente
efectuate cu aparatura moderna au confirmat relatia (6.19), permitand masurarea
sarcinii electrice elementare cu o precizie foarte buna:
.
Din valoarea sarcinii specifice ale electronului se obtine masa de repaus a electronului:
.
Asadar, la sfarsitul secolului XIX si inceputul secolului XX s-a demonstrat cu certitudine structura discontinua a substantei si sarcinii electrice.
Exemplul 1
La aplicarea unei tensiuni
intre armaturile unui
condensator plan se observa ca o
picatura sferica de ulei plasata intre armaturi se deplaseaza in sus cu viteza
constanta 
. Aplicand tensiunea 
de sens opus se
observa ca picatura de ulei se deplaseaza in jos cu viteza constanta 
. Sa se determine sarcina electrica a picaturii, cunoscand
densitatea uleiului 
, densitatea aerului 
, distanta intre armaturi 
si coeficientul de
viscozitate dinamica .
Rezolvare
Conditiile de echilibru, in fiecare din cele doua cazuri, sunt:
Inlocuind expresiile fortelor, se obtine sistemul de ecuatii:
Eliminand raza a picaturii se obtine
sarcina :
.
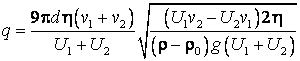6.3 Natura electromagnetica a luminii
Inca din a doua jumatate a secolului al XVII-lea, pe timpul lui Newton si Huygens, pentru explicarea naturii luminii s-au conturat doua teorii diametral opuse. Newton a fost adeptul teoriei corpusculare a luminii, fara sa reuseasca stabilirea precisa a naturii corpusculilor care se deplaseaza in linie dreapta de la sursa la observator, provocand efectele luminoase. La polul opus, Huygens a propus explicarea fenomenelor legate de propagarea luminii plecand de la conceptia ondulatorie asupra naturii acesteia.
Pentru a decide definitiv in favoarea uneia sau alteia dintre aceste conceptii se impunea gasirea unui fapt experimental crucial. Acesta s-a dovedit a fi legat de viteza de propagare a luminii in vid, respectiv in medii mai dense ca apa sau sticla. In cadrul teoriei corpusculare asupra naturii luminii se considera ca viteza de propagare a luminii in medii mai dense trebuie sa fie mai mare decat in vid, in timp ce teoria ondulatorie prezicea ca viteza de propagare a luminii in vid trebuie sa fie mai mare decat in alte medii, ca apa sau sticla.
Date experimentale au aratat ca viteza luminii in apa este mai mica decat in aer, ceea ce a constituit o dovada esentiala in favoarea naturii ondulatorii a luminii. Fenomenele de interferenta a luminii au contribuit de asemenea la consolidarea conceptiei ondulatorii. Alte fenomene ca polarizarea luminii si birefringenta au scos in evidenta faptul ca lumina trebuie sa fie o unda transversala, adica directia de vibratie sa fie perpendiculara pe directia de propagare. Teoria ondulatorie a luminii parea sa fie singura in masura sa explice fenomenele cunoscute pana la sfarsitul secolului XIX. Cu toate acestea, ramanea nerezolvat un aspect fundamental, si anume natura undelor ce reprezinta lumina.
Multa vreme s-a considerat ca undele luminoase sunt analoage cu undele transversale care se propaga intr-un mediu elastic. De aici a aparut necesitatea imaginarii unui mediu in care se propaga vibratiile corespunzatoare undelor luminoase. Asa cum s-a aratat la teoria relativitatii restranse, acest mediu cunoscut sub denumirea de eter trebuia sa aiba proprietati contradictorii: sa umple intreg spatiul, fiind in acelasi timp transparent. In fapt, tocmai aceste proprietati greu de imaginat ale eterului l-au facut pe Newton sa nu accepte conceptia ondulatorie asupra naturii luminii, deoarece corpusculii se pot deplasa in vid fara dificultati, in timp ce unda se propaga numai intr-un mediu elastic.
Intre anii 1864 si 1873 Maxwell s-a ocupat de perfectionarea teoriei electromagnetismului. Aceasta cunoscuse deja succese remarcabile, in special dupa descoperirea lui Öersted din anul 1820, conform careia un curent electric genereaza camp magnetic, precum si descoperirea de catre Faraday, in anul 1831, a fenomenului de inductie electromagnetica.
Maxwell a reusit sa obtina ecuatiile campului
electromagnetic, adica un sistem de ecuatii diferentiale care exprima legatura
dintre vectorii caracteristici campului electromagnetic (intensitatea campului
electric 
si intensitatea campului
magnetic 
) si sursele campului (densitatea de sarcina si densitatea de
curent electric 
). Pe baza ecuatiilor obtinute de Maxwell se ajunge la
concluzia ca orice perturbatie a campului electromagnetic se propaga in vid,
respectiv in dielectrici, sub forma de unda electromagnetica. Pentru viteza de
propagare a undelor electromagnetice s-a obtinut formula:
, (6.20)
unde
(6.21)
este viteza undelor
electromagnetice in vid. Pe baza mai multor experiente efectuate inainte ca
Maxwell sa obtina acest rezultat, care au aratat ca viteza luminii in vid este
egala cu 
, Maxwell ajunge la concluzia ca lumina este o unda
electromagnetica.
Pentru vid si dielectrici
permeabilitatea relativa 
, astfel ca viteza de propagare a luminii intr-un mediu
dielectric oarecare este:
, (6.22)
unde 
este indicele de
refractie al mediului respectiv. Insa permitivitatea relativa
, de unde 
, astfel ca viteza luminii - ca unda electromagnetica - intr-un
mediu dielectric oarecare este mai mica decat viteza luminii in vid, ceea ce
este in perfecta concordanta cu datele experimentale.
Prin unele experiente efectuate intre anii 1887 si 1889 fizicianul german
Heinrich Rudolf Hertz (1857-1894) a dovedit existenta undelor electromagnetice,
precum si faptul ca proprietatile acestor unde sunt cele care rezulta din
teoria lui Maxwell. Comunicatiile moderne - radio si TV - reprezinta rezultate
practice ale dezvoltarii lucrarilor efectuate de Maxwell si Hertz. Nu ne vom
opri aici asupra formei generale a ecuatiilor lui Maxwell, ci subliniem numai concluzia
ca orice camp electric variabil in timp genereaza camp magnetic, dupa cum un camp
magnetic variabil in timp genereaza camp electric.
In cazul simplu al
unui camp electric cu intensitatea variabila in timp,
orientata paralel cu axa
, va lua nastere un camp magnetic cu intensitatea orientata paralel cu axa 
(fig.3). Considerand un
mediu dielectric cu rezistivitatea 
, ecuatiile lui Maxwell pentru o astfel de situatie capata
forma:
(6.23)
Derivand prima ecuatie in raport cu 
si a doua in raport cu 
, obtinem:
, (6.24)
de unde rezulta
(6.25)
Analog se obtine ecuatia pentru campul electric al undei
(6.26)
Ecuatiile diferentiale (6.25) si (6.26)
reprezinta ecuatiile de propagare a undelor electromagnetice plane in lungul
axei 
. Se poate observa ca 
are dimensiunea unei
viteze la patrat, ceea ce conduce la formula (6.20), si astfel ecuatiile
diferentiale (6.25) si (6.26) iau forma:
(6.27)
(6.28)
Solutiile, care prin inlocuire directa verifica ecuatiile diferentiale (6.27) si (6.28), sunt de forma:
(6.29)
(6.30)
unde a este o constanta ce caracterizeaza
unda electromagnetica respectiva, iar 
este faza initiala. Introducand
solutiile (6.29) si (6.30) in ecuatiile lui Maxwell (6.23) obtinem 
, ceea ce inseamna ca vectorii si oscileaza in faza.
Deoarece solutiile (6.29) si (6.30) sunt functii periodice atat in raport cu
timpul , cat si in raport cu distanta , se impun egalitatile:
(6.31)
, (6.32)
unde este perioada, iar 
lungimea de unda a
undei electromagnetice.
Din (6.31) obtinem:
(6.33)
semnificatia marimii 
fiind de pulsatie a
undei. Din (6.32) si (6.33) obtinem:
(6.34)
Ecuatiile (6.29) si (6.30) devin:
(6.35)
(6.36)
Introducand solutiile (6.35)
si (6.36) in ecuatiile Maxwell (6.23), ajungem la concluzia ca modulele
vectorilor si nu sunt independente, ele
fiind legate prin relatia:
(6.37)
Vectorii si ai undei electromagnetice
fiind in faza, normali unul pe celalalt, ca si pe directia de propagare a
undei, inseamna ca unda este transversala (fig.4). Experimental a fost dovedit faptul
ca fenomenele optice, efectele fiziologice etc., se datoreaza in special vectorului
electric .
Unda electromagnetica transporta energie. Se stie ca densitatea de energie (energia unitatii de volum) pentru campul electric si magnetic se exprima prin:
(6.38)
si
(6.39)
Tinand seama de (6.37), obtinem densitatea de energie a campului electromagnetic:
(6.40)
sau
(6.41)
Ne intereseaza
valoarea medie a densitatii de energie 
, a carei formula este:
(6.42)
Am utilizat
cunoscuta valoare 
pentru valoarea medie
a lui cos2.
Intensitatea 
a unei unde
electromagnetice este energia transportata de unda in unitatea de timp prin
unitatea de arie a unei suprafete perpendiculara pe directia de propagare a
undei. Se demonstreaza simplu relatia:
(6.43)
Intensitatea undei electromagnetice este proportionala cu patratul amplitutdinii vectorului intensitatea campului electric, care se numeste adesea vector luminos.
6.4 Generarea undelor electromagnetice
In electrodinamica clasica
se demonstreaza ca orice purtator de sarcina electrica care se deplaseaza
accelerat radiaza energie sub forma de unde electromagnetice. Consideram un
purtator de sarcina electrica punctiform, care se
deplaseaza in vid cu acceleratia (fig.5). In cazul
nerelativist, la distante suficient de mari de purtatorul de sarcina electrica,
vectorii si se exprima astfel:
(6.44)
(6.45)
Aceste expresii pentru intensitatile campului electric si magnetic generat de purtatorul punctiform de sarcina sunt valabile pentru distante care indeplinesc conditia:
(6.46)
Din (6.44) si (6.42) rezulta ca
vectorii 
,
si 
sunt perpendiculari intre
ei. In consecinta, o sarcina electrica care se deplaseaza accelerat genereaza,
la distante suficient de mari, o
unda electromagnetica sferica in care vibratiile vectorilor si sunt perpendiculare pe
directia de propagare a undei.
Densitatea de energie a campului electromagnetic corespunzator undei electromagnetice este:
(6.47)
Sa calculam energia undelor
electromagnetice generate de sarcina electrica in miscarea sa
accelerata, in intervalul de timp cuprins intre momentul 
si momentul
.
La momentul campul electromagnetic
generat de sarcina electrica in intervalul de timp cuprins intre si 
se va afla intre
sferele de raze 
si 
, asa cum se poate vedea in fig.6.
In principiu, sferele 
si 
nu sunt concentrice,
deoarece centrele lor coincid cu pozitiile sarcinii electrice la momentele si . Viteza particulei fiind mult mai mica
decat viteza undelor electromagnetice in vid, putem considera ca sferele sunt
concentrice. Energia totala a undelor electromagnetice generate de catre
particula in intervalul de timp 
este:
)
Volumul 
este volumul cuprins intre
sferele si , iar grosimea stratului sferic este 
. Elementul de volum va fi 
, unde 
reprezinta elementul
de arie in coordonate sferice. Din (6.48) obtinem:
,
de unde
(6.49)
Se ajunge astfel la concluzia ca orice particula incarcata cu sarcina electrica, ce se deplaseaza accelerat, emite radiatii sub forma de unda electromagnetica, iar energia emisa in unitatea de timp este proportionala cu patratul sarcinii electrice si cu patratul acceleratiei.
6.5 Structura discontinua a radiatiei electromagnetice.
Teoria electromagnetica a luminii a permis intelegerea unei clase destul de mari de fenomene fizice ca difractia, interferenta, polarizarea luminii etc.
Exista insa multe alte fenomene care nu pot fi intelese plecand de la teoria electromagnetica a luminii. Pentru explicarea unor fenomene cum ar fi efectul fotoelectric, efectul Compton etc., este necesar sa avem o conceptie corpusculara asupra naturii luminii, sa admitem ca lumina este un flux de fotoni, adica are o structura discontinua.
Stadiul distributiei energiei in spectrul de emisie al corpului absolut negru, aflat in echilibru termic cu radiatia emisa de acesta, a condus la ipoteza privind caracterul discontinuu al emisiei si absorbtiei luminii, in portii finite de energie, care au fost numite cuante de lumina (mai exact - fotoni).
Energia unui foton este data de relatia:
, (6.50)
unde 
si 
sunt constantele lui
Planck.
Intre energiea 
si impulsul al fotonului exista
relatia relativista:
(6.51)
Masa de repaus a fotonului se considera
, si din (6.51) obtinem:
(6.52)
In cadrul teoriei
ondulatorii se introduce vectorul de unda , de modul
(6.53)
Vectorul de unda 
este orientat in
sensul propagarii undei, si deci in sensul impulsului 
al fotonului. Astfel,
formula (6.52) poate fi scrisa vectorial:
(6.54)
Relatiile(6.50) si (6.54) reprezinta formulele fundamentale ale teoriei cuantice pentru undele electromagnetice.
Intuitiv, si deci fara pretentii de
rigurozitate, ne putem imagina lumina ca un gaz format din particule de energie
si impulsul 
. Nu este prea important cat de corecta este aceasta afirmatie,
esential este sa intelegem ca schimbul de energie si impuls intre microsisteme si
undele electromagnetice (lumina) se face pe calea generarii si respectiv absorbtiei
de fotoni. Aceasta idee este fundamentala in aplicarea legilor de conservare
pentru energie si impuls in cazul unui sistem de microparticule aflat in
interactiune cu lumina. Tot intuitiv se vorbeste de "ciocniri" dintre foton si
microparticula.
Consideram ca microsistemul (atom,
molecula, electron etc.) a avut energia 
si impulsul 
inaintea "ciocnirii"
cu fotonul, si respectiv energia 
si impulsul 
dupa "ciocnire".
Fotonul a avut energia 
si impulsul inainte de "ciocnire",
respectiv energia 
si 
dupa "ciocnire".
Sensul mai exact al acestei interactiuni pe care am numit-o "ciocnire" este acela
ca a disparut un foton de energie si impuls si a aparut un foton de
energie ' si impuls .
Tendinta de apropiere de limbajul clasic a condus la aproximarea conform careia fotonul "ciocnindu-se" cu microsistemul considerat, si-a schimbat energia si impulsul.
Asadar, pentru procesul de interactiune dintre microparticula si foton, legile de conservare a energiei si impulsului se scriu sub forma:
(6.55)
(6.56)
Aceste ecuatii contin cele trei procese fundamentale, si anume:
a) 
absorbtia unui foton;
b) 
emisia unui foton;
c) 
difuzia fotonului.
In conceptia clasica,
ondulatorie, energia exprimata prin intensitatea undei (6.43) este proportionala
cu patratul amplitudinii intensitatii campului electric, in timp ce in conceptia
cuantica lumina este formata din fotoni care au o energie proportionala cu
frecventa 
. Deoarece nu exista nici o relatie generala intre
amplitudine si frecventa, cele doua conceptii sunt ireductibile. In acelasi
timp, nu se poate afirma ca teoria fotonica exclude total conceptia
ondulatorie, deoarece energia si impulsul fotonului depind de marimi ca frecventa
si lungimea de unda , care nu pot fi intelese decat in cadrul teoriei
ondulatorii.
Ne vom opri la cateva aspecte privind verificarea experimentala a legilor de conservare (6.55) si (6.56).
Exemplul 2
Sa se demonstreze ca:
a) un electron aflat in repaus in vid nu poate absorbi completun foton;
b) un electron liber in vid nu poate emite un foton.
Rezolvare
a) Aplicam legile de conservare pentru energia totala si impuls in cazul interactiei electron-foton:
,
de unde prin
eliminarea lungimii de unda a fotonului, tinand
cont si de formula relativista a variatiei masei cu viteza, se obtin solutiile:
, sau 
.
b) In acest caz legile de conservare au forma urmatoare:
(6.57)
, (6.58)
unde
este versorul
directiei de miscare a electronului, pe care o va avea in urma emisiei
fotonului (fig.7). Se ridica cele doua relatii la puterea a doua si apoi se
impart:
, (6.59)
unde
si 
. (6.60)
Din
(3) se obtin succesiv relatiile: 
; 
, de unde:
(6.61)
Ridicand la patrat relatia (6.58) si introducand (6.61), obtinem:
(6.62)
Introducand expresiile lui si din (6.60) in (6.62)
si efectuand calcule simple, se obtine in final:
(6.63)
Deoarece rezultatul obtinut incalca postulatul referitor la viteza luminii in vid, inseamna ca am demonstrat ca un un electron liber in vid nu poate emite un foton.
6.5.1 Efectul fotoelectric
Efectul fotoelectric a fost descoperit experimental de H. Hertz in anul 1888. Acesta a observat ca producerea unei scantei intre doua sfere de zinc ale unui eclator este favorizata daca suprafata uneia dintre sfere este iluminata cu radiatii din domeniul ultraviolet. Studiile ulterioare au aratat ca exista urmatoarele tipuri de efecte fotoelectrice:
1. Efectul fotoelectric extern, care consta in emisia de electroni in afara unui corp metalic, la iradierea suprafetei acestuia cu unde electromagnetice adecvate.
2. Efectul fotoelectric intern - marirea, ca urmare a absorbtiei undelor electromagnetice, a numarului de electroni "liberi" in interiorul unui corp iradiat, nu insa si emisia electronilor in afara corpului. Principala consecinta a absorbtiei este micsorarea substantiala a rezistentei electrice a probei iradiate.
3. Efectul fotogalvanic - aparitia, sub influenta iradierii, a unei tensiuni electromotoare la contactul dintre un semiconductor si un metal, sau dintre doua semiconductoare.
4. Fotoionizarea moleculelor sau a atomilor sub actiunea luminii incidente, intr-un mediu gazos.
1. Efectul fotoelectric extern si legile sale le vom studia in detaliu in cele ce urmeaza.
Schema tipica a instalatiei
utilizate pentru studiul experimental al efectului fotolelectric extern poate
fi vazuta in fig.8. In tubul de sticla se sudeaza o fereastra
de cuart , acest material fiind transparent pentru radiatiile
ultraviolete ce provin de la sursa 
.
Anodul este de forma unui
cilindru in care se practica o deschidere, in scopul de a facilita ajungerea
radiatiilor pe suprafata catodului 
. Fotocatodul este legat la borna
negativa a bateriei , iar anodul la borna pozitiva. Reostatul asigura o cadere de
tensiune variabila intre catod si anod, iar galvanometrul 
masoara intensitatea a curentului electric
prin circuit. In tubul de sticla se face vid.
Datorita electronilor emisi de catod la iluminarea catodului (denumiti in continuare
fotoelectroni), in circuit va apare sub
actiunea luminii un curent electric continuu (denumit curent fotoelectric, sau fotocurent).
Mentinand nemodificate intensitatea si structura spectrala a radiatiei
incidente pe catod, se obtine o dependenta intensitatii fotocurentului de caderea de tensiune
dintre catod si anod
ca in fig.9. Constatam ca pentru o anume valoare 
se ajunge la un curent
de saturatie cu intensitatea 
. Acesta
corespunde situatiei cand toti electronii emisi de fotocatod ajung la anod. In
fapt, intensitatea curentului de saturatie este masura efectului
fotoelectric al fluxului de radiatie dat.
Mentinand structura spectrala a radiatiei incidente, dar variind
intensitatea acesteia, se obtine o familie de curbe ca in fig.10, indicand
faptul ca intensitatea curentului de saturatie este proportionala cu
intensitatea radiatiei incidente .
Din fig.9 si fig.10 se vede ca pentru 
intensitatea
curentului fotoelectric 
, ceea ce dovedeste faptul ca electronii scosi din fotocatod
au o viteza initiala 
, respectiv o energie cinetica 
, si astfel pot atinge anodul fara a fi necesar un camp
electric intre catod si anod. Pentru intreruperea curentului electric din
circuit este necesara o tensiune de franare 
negativa. Forma
curbelor din fig.9 si fig.10 indica faptul ca fotoelectronii emisi din catod au
viteze diferite. Aceasta se explica prin faptul ca electronii parasesc suprafata
fotocatodului, precum si unele straturi din interiorul acestuia. Fotoelectronii
din straturile mai adanci ale fotocatodului pierd energii diferite 
pana ajung la suprafata
acestuia. Pentru tensiunea negativa 
vor fi franati
electronii si cei mai rapizi, are au parasit fotocatodul cu viteza maxima 
, pentru care este indeplinita relatia:
, (6.64)
unde 
este masa de repaus a
electronului.
Din (6.64) se pot determina
experimental viteza maxima si energia cinetica maxima a electronilor.
Rezultatele experimentale sintetizate in fig.11 indica independenta marimilor si 
de intensitatea luminii incidente.
Mentinand constanta intensitatea radiatiei
incidente, insa schimbandu-i frecventa (respectiv lungimea de
unda ), se obtine ca energia cinetica maxima a fotoelectronilor
este proportionala cu frecventa ( fig.10).
Din aceste experiente apare o noua
caracteristica a efectului fotoelectric extern,
si anume: efectul fotoelectric nu are are loc daca frecventa radiatiei
incidente este mai mica decat o anumita limita 
. Valorile si
respectiv 
reprezinta pragul rosu
al efectului fotoelectric si depind de natura materialului din care este confectionat
catodul.
Toate aceste date experimentale sunt sintetizate in urmatoarele legi
empirice ale efectului fotoelectric:
1. Pentru o compozitie spectrala constanta a radiatiei incidente intensitatea fotocurentului este direct proportionala cu intensitatea radiatiei incidente pe catod.
2. Energia cinetica initiala a electronilor scosi de radiatia electromagnetica din catod creste liniar cu frecventa radiatiei si nu depinde de intensitatea acesteia.
3. Efectul fotoelectric nu apare daca frecventa radiatiei
incidente este mai mica decat o valoare caracteristica pentru fiecare metal , numita pragul rosu.
4. Efectul fotoelctric nu prezinta inertie, adica
intervalul de timp dintre momentul inceperii iradierii si momentul inceperii
emisiei de electroni este neglijabil 
.
Teoria electromagnetica a luminii nu poate explica urmatoarele fapte experimentale:
- prezenta pragului rosu al efectului fotoelectric;
- independenta energiei cinetice initiale
a fotoelectronilor de intensitatea 
a fluxului de fotoni incidenti;
- lipsa unui interval finit de timp intre momentul inceperii iradierii si momentul inceperii emisiei de electroni de catre fotocatod.
In anul 1905, cunoscutul fizician american
de origine germana Albert Einstein (1879-1955) a propus o noua interpretare a
efectului fotoelectric. Dupa Einstein, lumina monocromatica de frecventa se emite, absoarbe si propaga ca un flux de
fotoni care au fiecare energia 
. Din acest punct de vedere, intensitatea a luminii ce cade pe fotocatod este determinata
de numarul de fotoni ce cad in unitatea de timp pe unitatea de arie a suprafetei
catodului, iar energia fiecarui foton este determinata de frecventa a radiatii.
In cazul efectului fotoelectric
fotonul se "ciocneste" cu electronul, cedandu-i acestuia intreaga sa enrgie . Electronul care primeste aceasta energie si se indreapta
spre suprafata metalului poate cheltui o parte 
din energia sa in ciocnirile
inelastice din interiorul metalului, si o alta energie 
(lucrul mecanic
de extractie ) pentru a iesi din metal. Energia care ii mai ramane electronului
in momentul in care paraseste suprafata metalului reprezinta energia lui
cinetica. Din legea conservarii energiei rezulta:
(6.65)
Daca 
, adica electronul nu pierde energie prin ciocniri in
interiorul metalului, energia sa cinetica maxima va fi:
(6.66)
Relatiile (6.65) si (6.66) reprezinta forma matematica a legii lui Einstein pentru efectul foroelectric extern. Formula (6.59) este verificata foarte bine de datele experimentale.
Existenta pragului
rosu al efectului fotoelectric extern este o consecinta directa a formulei (6.66).
Din 
, rezulta 
, deci exista o frecventa
,
astfel incat pentru 
efectul fotoelectric
extern nu poate avea loc. Aceasta teorie propusa de Einstein explica excelent
cele 4 legi empirice ale efectului fotoelectric extern. Din numarul de fotoni
ce cad pe suprafata fotocatodului numai
o mica parte (~1%) scot electronul de la suprafata metalului, iar restul cedeaza
energia atomilor metalului, incalzindu-l. Lipsa de inertie a efectului
fotoelectric se explica prin faptul ca transferul de energie de la foton la
electron se face practic instantaneu.
Efectul
fotoelectric extern are multe aplicatii in tehnica prin constructia celulelor
fotoelectrice. Acestea constau dintr-un fotocatod , bun emitator de electroni, si un anod ce colecteaza acesti
electroni (fig.12). In fotocelulele moderne se utilizeaza catozi complecsi cu
cesiu, care ajung la o sensibilitate de 
.
Legile de conservare pentru energie si
impuls arata ca daca electronul este liber (slab legat), nu poate avea loc o
absortie totala a energiei fotonului, ci numai o difuzie a acestuia. Sectiunea
eficace a efectului fotoelectric depinde de energia a fotonului si de numarul
de ordine al elementului chimic - metalului din care este facut catodul 
.
2. Efectul fotoelectric intern apare prin iluminarea unor materiale semiconductoare sau dielectrice, cand electronii eliberati de legaturile lor raman in interiorul materialului respectiv, influentand conductibilitatea acestuia. Conditia ca efecctul sa apara este ca energia fotonilor incidenti sa fie mai mare decat diferenta dintre energia corespunzatoare marginii de jos a benzii de conductie a semiconductorului, si energia corespunzatoare marginii de sus a benzii de valenta. Astfel, electronii blocati in banda de valenta vor trece sub forma de electroni liberi in banda de conductie, iar prezenta acestor purtatori aditionali de sarcina va creste conductivitatea semiconductorului, de unde si denumirea de efect fotoconductiv.
Cand semiconductorul (S.C.) este
iluminat, fiind legat prin fire conductoare la o sursa de tensiune si la un
galvanometru, apare un curent electric. La incetarea iluminarii, curentul scade
la valoarea sa de intuneric, apropiata de zero. La metale nu se observa acest
efect, deoarece densitatea de electroni "liberi" in stare normala este extrem
de mare. Efectul fotoelectric 
intern se foloseste la construirea fotorezistentelor
(fig.13), care constau dintr-o placa suport de sticla, pe care se depune un
strat subtire de semiconductor, la suprafata caruia se fixeaza electrozi din
material semiconductor ce formeaza contacte
ohmice (fig.13). Spre deosebire de efectul fotoelectric extern, la
fotorezistentele construite pe baza efectului fotoelectric intern nu apare
curent de saturatie, caracteristica curent tensiune fiind de forma aratata in
fig.14. Se constata ca 
este proportional cu
tensiunea aplicata intre
electrozi. Astfel, intensitatea a curentului
fotoelectric nu depinde numai de intensitatea radiatiei, ci si de tensiunea
intre electrozi.
Sensibilitatea fotorezistentelor, definit ca
raportul dintre intensitatea fotocurentului electric si intensitatea a radiatiei incidente,
este de mii de ori mai mare decat sensibilitatea celulelor fotoelectrice, care
sunt aplicatii tehnice ale efectului fotoelectric extern. Acest fapt se
datoreaza castigului fotoconductiv,
care se defineste ca raportul intre numarul de electroni colectati la unul din
electrozi per foton incident. Castigul apare datorita vitezelor diferite prin
materialul semiconductor a electronului si golului formate de fotonii
incidenti. Electronul se deplaseaza de obicei cu viteza mult mai mari decat
golul, traversand semiconductorul si fiind colectat la contactul pozitiv.
Aceasta dtermina introducerea unui alt electron la contactul negativ, in timp
ce golul inca nu a ajuns la contactul negativ. In final, golul ajunge la
contactul negativ, fiind colectat in circuitul extern. Astfel, pentru o pereche
electron-gol creata, un numar mai mare de electroni ajung in circuitul
exterior, iar durata procesului fotoconductiv este determinata de timpul de
tranzit al purtatorului mai lent, adica golul.
Dependenta intensitatii curentului
fotoelectric prin fotorezistenta
de intensitatea a radiatiei
incidente nu este liniara (fig.15), asa
cum se intampla la efectul fotoelectric extern. Aceasta abatere de la
liniaritate se datoreaza faptului ca efectul fotoelectric intern este insotit
de o serie de efecte colaterale, cum ar fi procesul de recombinare
electron-gol. In general, dependenta este de forma:
, (6.68)
unde 
si 
sunt constante, iar 
.
Se constata de asemenea ca procesele
fotoelectrice in fotoreziatenta poseda inertie, astfel ca intensitatea
fotocurentului nu atinge instantaneu valoarea corespunzatoare intensitatii
radiatiei incidente, iar prin intreruperea brusca a iluminarii intensitatea
fotocurentului scade lent spre valoarea corespunzatoare curentului de
intuneric. Aceasta inertie se explica prin faptul ca electronii eliberati de
radiatia incidenta din legaturile lor se vor afla in stare "libera" numai un
timp 
, numit timpul de viata al fotoelectronilor. Acest timp este
cuprins intre 
, depinzand de materialul fotorezistiv utilizat. Toti
electronii se recopmbina, in medie dupa timpul , trecand din nou in starea legata.
La inceputul iluminarii numarul de
fotoelectroni formati depaseste numarul recombinarilor, ceea ce conduce la o
crestere a fotocurentului. Dupa timpul se stabileste un
echilibru dinamic intre numarul de electroni eliberati si numarul de electroni
care se recombina. Intensitatea fotocurentului va atinge astfel valoarea sa
maxima, corespunzatoare radiatiei incidente. Dupa intreruperea iluminarii,
electronii se recombina de asemenea dupa un timp mediu de viata .
3. Efectul fotovoltaic consta in aparitia unei tensiuni electromotoare daca suprafata de separare dintre un semiconductor si un metal este iradiata cu radiatie electromagnetica.
Pe o placa de cupru (1) se
depune un start subtire de oxid de cupru (2), de ordinul zecimilor de
milimetru, pe care se depune un strat metalic subtire, transparent (3), ca in
fig.15. Iluminand stratul de oxid de cupru, se formeaza electroni liberi ca
urmare a efectului fotoelectric intern. La suprafata de separare dintre Cu si
Cu2O exista un strat foarte subtire, cu grosimea 
, care poseda proprietatea de redresare. Acest strat permite
trecerea electronilor nmai intr-un singur sens, de la Cu2O la Cu,
astfel ca placa de cupru se incarca negativ, iarstratul semiconductor de Cu2O
se incarca pozitiv. Apare astfel o diferenta de potential intre cele doua
straturi, care se mentine atata timp cat iradierea continua. In circuitul
exterior va apare un curent continuu cu sensul de la Cu2O la Cu.
In cazul efectului fotovoltaic se
petrece o transformare directa a energiei undelor electromagnetice din domeniul
optic, in energie electrica. Sensibilitatea poate atinge 
. Pe baza efectului fotovoltaic se construiesc celulele solare, care au atins un
randament de 
, si care prezinta mai multe avantaje: nu polueaza, au timp
de viata practic nelimitat, pot functiona in conditii atmosferice variate etc.
Exemplul 3
Fotoelectronii emisi de un catod metalic sub
actiunea radiatiilor cu lungimile de unda 
si 
sunt franati de
tensiunile anodice 
, respectiv 
. Cunoscand sarcina electronului 
si viteza luminii in
vid 
, sa se determine:
a) Constanta lui Planck;
b) Lucrul mecanic de extractie 
;
c) Frecventa de prag a efectului 
.
Rezolvare
Din (6.64) si (6.66) obtinem:
Particularizand pentru cele doua lungimi de unda obtinem sistemul de ecuatii:
Eliminand 
, se obtine expresia constantei lui Planck:
.
Eliminand 
, se obtine expresia lucrului de extractie:
c) Din conditia de prag:
,
Inlocuind expresiile obtinute la punctele a) si
b) pentru si , obtinem frecventa de
prag:
.
Exemplu 4
Suprafata
unui metal este iluminata cu o radiatie luminoasa avand lungimea de unda 
, caz in care tensiunea de franare are o anumita valoare.
Micsorand lungimea de unda cu 
, pentru a taia din nou fotocurentul diferenta de potential
trebuie sa creasca cu 
. Sa se determine valoarea sarcinii electronului.
Rezolvare
de unde se obtine:
.
6.5.2 Efectul Compton
Acest efect, descoperit de A. Compton in anul 1923, consta
in schimbarea lungimii de unda a razelor X in procesul de difuzie a acestora pe
atomi usori. Din punctul de vedere al teoriei electromagnetice a luminii, difuzia
razelor X ar trebui sa fie legata de oscilatiile fortate ale electronilor din
substanta, iar frecventa luminii difuzate (ca si lungimea de unda) ar trebui sa
fie aceeasi cu cea a luminii incidente. Compton a observat insa experimental ca
in lumina difuzata, pe langa radiatia cu lungimea de unda 
a radiatiei incidente
mai aprare o radiatie cu lungimeq de unda 
.
Daca atomii mediului difuzat sunt usori (numarul de
ordine 
este mic), electronii
periferici sunt slab legati de nucleu, si deci putem considera intr-o prima aproximatie
ca acesti electroni de valenta sunt liberi. Notiunea de electron liber in acest
caz este relativa, si se refera la faptul ca energia de legatura a electronului
in atom este mult mai mica decat energia fotonului incident. Asadar, efectul
Compton poate fi considerat ca difuzia unui foton pe un electron liber. Acest proces de "ciocnire"
electron-foton poate fi tratat pe baza legilor de conservare (6.55) si (6.56). Deoarece electronul
are masa foarte mica, legile de conservare trebuie scrise in termeni relativisti.
Consideram ca un electron aflat in
repaus, avand energia 
si impulsul 
, este ciocnit de un foton cu energia initiala 
si impulsul 
(unde 
). In urama "ciocnirii" fotonul isi modifica directia
de miscare, energia si impulsul (fig.16), iar electronul poate capata o viteza
apropiata de viteza luminii in vid . Legile de conservare (6.55) si (6.56) vor lua in acest caz
forma:
( 6.69)
(6.70)
Scriind teorema lui Pitagora generalizata in triunghiul ABC (fig.16), se obtine:
(6.71)
Din (6.69) obtinem:
,
apoi ridicam relatia la patrat:
(6.72)
Scazand (6.71) din (6.72) obtinem:
sau
(6.73)
Din dependenta relativista a masei de viteza, 
, obtinem:
(6.74)
Tinand cont de (6.74), (6.73) devine:
sau
(6.75)
Trecand de la frecventele si la lungimile de unda
corespunzatoare 
; 
, (6.75 ) devine:
,
de unde
(6.76)
Marimea:
(6.77)
este cunoscuta sub denumirea de lungime de unda Compton.
Valoarea foarte mica a lungimii de unda Compton explica
faptul ca acest efect nu poate fi observat pentru lumina din domeniul vizibil. Pentru
o
lungime de unda 
Å este imposibil de sesizat experimental o deplasare 
Å, In schimb,
pentru razele X (care au lungimea de
unda cuprinsa intre 0,1Å si 1Å) 
este comparabila cu , si deci poate fi masurata relativ usor. Independenta marimii de natura substantei
difuzate este o consecinta a ipotezei initiale, si anume ca difuzia
Formula (6.76) obtinuta de Compton este in totala concordanta cu datele experimentale.
Se constata ca odata cu cresterea numarului de ordine Z al materialului difuzant, intensitatea
liniei deplasate (cu lungimea de unda ) scade, iar intensitatea liniei nedeplasate (cu lungimea de
unda ) creste (fig.17 a). Pentru materialele difuzante usoare ca
Li, B, Be (fig.17 b), prin difuzie se obtine practic numai linia deplasata cu
lungimea de unda 
.
In cazul elementelor ceva mai grele ca
Al, Si (fig.17 c), incepe sa apara si linia nedeplasata, iar pentru materiale
mai grele ca Fe, Ni, Cu (fig.17 d), linia nedeplasata are o intensitate mai
mare decat cea deplasata.
Calculul efectuat in ipoteza electronilor liberi este
corect numai pentru atomii usori, cu Z
mic. Pentru atomii cu Z suficient de
mare pot fi considerati liberi numai electronii de valenta. Daca fotonul
"ciocneste" un electron de pe paturile interioare ale atomului, adica un
electron practic legat, schimbul de energie si de impuls are loc intre foton si
atomul ca intreg. In acest caz, in formula (6.76) ar trebui introdusa in locul
masei de repaus a electronului masa de repaus a atomului, 
. Cum insa este de 103÷104
ori mai mare decat masa electronului, este clar ca 
. Astfel, raportul dintre intensitatea liniei cu lungimea de
unda si intensitatea liniei
cu lungimea de unda este egal cu raportul dintre
numarul electronilor de valenta si numarul electronilor din paturile interioare
ale atomului.
In efectul Compton electronul primeste de la fotonul incident energia:
(6.78)
Din (6.78) obtiem:
(6.79)
sau
(6.80)
In concluzie, electronul de recul primeste un procent
destul de mic din energia fotonului incident, . Aceast fapt permite deosebirea experimentala a electronilor
Compton de fotoelectroni, care au energia practic egala cu energia cuantei
incidente (vezi
formula 6.66).
Exemplul 5
Radiatia
de lungime de unda 
sufera o difuzie
Compton. Sa se determine:
a) Relatia dintre unghiul 
pe care-l face
directia fotonului difuzat cu directia fotonului incident si unghiul 
pe care-l face
directia electronului de recul cu directia fotonului incident;
b) Valoarea unghiului pentru cazul
particular 
si 
, cunoscand 
.
Rezolvare
a) Proiectam legea conservarii impulsului pe axele si (fig.13), obtinand
sistemul de ecuatii:
Eliminand din sistem viteza
electronului de recul, si inlocuind expresia lui din formula de
deplasare a lui Compton (6.75), obtinem relatia ceruta:
b) Particularizand formula obtinuta la
punctul a) cu datele de la punctul b) se obtine 
.
Exemplul 6
Intr-o experienta de tip
Compton energia fotonului incident se distribuie in mod egal intre fotonul
difuzat si electronul de recul, care se deplaseaza pe doua directii
perpendiculare intre ele. Cunoscand valoarea lungimii de unda Compton 
, sa se determine:
a) unghiul dintre directiile de miscare ale electronului de recul si fotonului incident.
b) lungimea de unda a fotonului difuzat;
Rezolvare
a) Cu notatiile din fig.13, conditiile problemei se scriu:
; 
.
Proiectand legea conservarii impulsului (6.69) pe axele Ox si Oy, obtinem:
,
de unde rezulta cu conditiile 
si
b) Din formula de deplasare a lui Compton (6.75)
, tinand cont ca si 
, se obtine:
.
Exemplul 7
Intr-un experiment de tip
Compton energia cinetica a electronilor de recul are valoarea 
. Sa se determine lungimea de unda a fotonilor incidenti care
au determinat reculul electronilor, cunoscand , 
si 
.
Rezolvare:
Din (6.80) obtinem energia cinetica a electronilor:
Valoarea maxima a energiei cinetice se obtine din conditia:
,
de unde se obtine 
. Inlocuind in expresia lui 
obtinem:
,
de unde obtinem o ecuatie de gradul doi
pentru :
Rezolvand ecuatia, se obtine: 
.
6.5.3 Difuzia luminii. Spectre Raman
Un numar mare de date experimentale arata ca in mediile omogene din punct de vedere optic lumina se propaga in linie dreapta. La trecerea unui fascicul de lumina printr-un mediu transparent se constata insa ca lumina se observa nu numai in directia incidentei, ci si in alte directii diferite. Acest fenomen este cunsocut sub numele de difuzia luminii sau imprastierea luminii.
Fizicianul si matematicianul englez John W. Rayleigh (1842-1919) a calculat intensitatea luminii difuzate sub diferite unghiuri, considerand ca difuzia luminii de catre mediile gazoase omogene se datoreste moleculelor gazului aflate intr-o miscare continua, haotica, de agiatie termica. Fizicianul rus Leonid Isaakovici Mandelstam (1879-1944) a aratat insa ca mediile omogne din punct de vedere optic nu pot difuza lumina, indiferent daca particulele lui componente se afla sau nu in miscare. Problema a fost rezolvata de catre fizicianul polonez Marian Smoluchowski (1878-1917), care a aratat ca difuzia luminii de catre mediile gazoase omogene se datoreaza fluctuatiilor densitatii gazului, fluctuatii ce au loc la orice temperatura diferita de 0 K.
Calculele efectuate in aceasta ipoteza conduc la o formula obtinuta initial de Rayleigh:
, (6.81)
cu urmatoarele semnificatii ale marimilor care intervin in formula:
- 
este intensitatea
luminii difuzata sub un unghi fata de directia
fasciculului incident de intensitate 
;
- este distanta de la
punctul in care are loc difuzia pana la punctul de observare a luminii
difuzate;
- este indicele de
refractie al mediului prin care are loc propagarea;
- este lungimea de unda
a radiatiei incidente;
- 
este elementul de
volum in care are loc difuzia;
- 
este numarul de
particule din unitatea de volum.
Formula (6.81), cunoscuta sub denumirea de formula lui Rayleigh, a fost obtinuta pornind de la natura electromagnetica a luminii. Aceasta formula prezinta o mare importanta, din mai multe puncte de vedere:
a) Masurarea intensitatii luminii difuzate in atmosfera
permite determinarea, pe baza formulei (6.81), a numarului de molecule din
unitatea de volum , si deci a numarului lui Avogadro. Datele experimentale efectuate
in acest sens conduc la valoarea 
molecule/mol. Acest rezultat confirma valabilitatea formulei (6.81)
b) Faptul ca 
i-a permis lui
Rayleigh sa explice culoarea albastra a cerului.
Culoarea albastra a cerului, ca si culoarea rosie a Soarelui la rasarit si la apus, se explica prin legitatea (6.81), adica prin faptul ca intensitatea luminii difuzate este invers proportionala cu lungimea de unda la puterea a patra. Daca nu ar avea loc difuzia luminii in atmosfera, Soarele si stelele ar aparea ca niste corpuri stralucitoare pe fondul unui cer negru. Cerul se vede luminos, mai corect albastru, datorita difuziei luminii in atmosfera. Cand Soarele se afla relativ aproape de orizont , la rasarit si apus, la noi ajung razele de lumina de la Soare slabite datorita difuziei in atmosfera. Deoarece difuzia este mai puternica in domeniul lungimilor de unda scurte, la noi ajunge cu precadere lumina din domeniul spectral cu lungimi de unda mari, si de aceea vedem Soarele rosu la rasarit si la apus.
Astfel, potrivit legii lui Rayleigh (6.81), difuzia luminii este cu atat mai puternica, cu cat lungimea de unda este mai mica, insa in procesul de difuzie lungimea de unda nu se modifica.
Fizicianul Indian C.V. Raman (1888-1970) a observant, in
anul 1928, ca in lumina difuzata, pe langa radiatiile cu aceeasi lungime de unda
ca si radiatiile
incidente, apar si radiatii cu alte lungimi de unda 
. S-a constatat ca diferentele 
nu depind de , insa variaza in functie de natura substantei difuzante. Fata
de teoria lui Rayleigh, apare in plus proprietatea ca deplasarile lungimii de
unda depind de structura moleculara a substantei imprastietoare.
Fenomenul Raman poate fi explicat complet numai pe baza teoriei corpusculare a luminii.
Coicnirea dintre un foton si o molecula poate fi elastica sau neelastica. In
cazul ciocnirii elastice fotonul isi schimba directia de miscare, dar nu-si
schimba energia, ceea ce explica invarianta lungimii de unda in procesul de
difuzie, conform cu legea lui Rayleigh. Daca insa ciocnirea este neelastica,
fotonul poate fie sa cedeze energie moleculei, fie sa primeasca energie de la
molecula (fig.18). Variatia energiei moleculei are loc numai prin tranzitii intre
nivelele cuantificate 
Astfel, in urma
difuziei inelastice frecventa radiatiei este:
(6.82)
sau
(6.83)
Liniile Raman deplasate spre frecventele mici (6.83) se numesc linii Stokes, iar cele deplasate spre frecvente mari (6.82) se numesc linii anti-Stokes.
Bibliografie
Richard P. Feynman, Robert B. Leighton and Matthew Sands. The Feynman Lectures on Physics, vol.I, Definitive edition, Addison-Wesley Publishing Company, Reading, Massachusetts, 2006.
Nicolae Barbulescu, Radu Titeica, s.a. Fizica, vol.II, Ed. Didactica si Pedagogica, 1971.
4. Thomas P. Pearsall. Photonics Essentials. McGraw-Hill, New York Chicago San Francisco Lisbon London Madrid Mexico-City Milan New Delhi San Juan Seoul Singapore Sydney Toronto, 2003.
Sean F.
Johnstone. A Hystory of Light and Colour
Measurement,
6. Mark Csele. Fundamentals of Light Sources and Lasers. Wiley-Interscience, A John Wiley & Sons, Inc., Publication, New Jersey, 2004.
Eyvind H. Wichmann. Fizica Cuantica, Cursul de Fizica Berkeley, vol.IV, Editura Didactica si Pedagogica, Bucuresti, 1983.
Radiatia termica si legile sale. (aici sau la cursul de laseri?)
|
