Suprafete de revolutie de arie minima (sau problema lui Plateau pentru suprafete de revolutie)
În spatiul tridimensional, R3 , se da un plan (P), o dreapta (d) (P) si doua puncte A si B (P), situate de aceeasi parte fata de dreapta (d).
Problema cere ca în multimea tuturor curbelor din planul (P), între punctele A si B, situate în acela# 111c22b 1;i semiplan cu punctele A si B, sa se determine curba pentru care aria suprafetei obtinuta prin rotirea acesteia în jurul dreptei (d), în spatiu, sa fie minima.
a) Modelul matematic al problemei.
Din
punct de vedere analitic consideram un sistem de coordonate în planul (P)
astfel încât dreapta (d) este axa absciselor iar A se afla pe axa
ordonatelor, cu ordonata y > fie (
,
) (0, y) coordonatele punctului B, 0 (deoarece, prin ipoteza, punctul B
este situat în acelasi semiplan cu A).
Vom considera cazul curbelor de clasa C1 pe portiuni, desi problema de analiza matematica care modeleaza problema de geometrie de mai sus are sens si pentru curbe absolut continue.
Pentru
punctul x0 = (,) R2
consideram multimea Xcp(x0) a tuturor functiilor
de clasa C1 pe portiuni, x( ) = (x1( ), x2( 0, tF(x( R2
cu urmatoarele proprietati:
x(0) = x0, x(tF(x( ))) = (0, y), x2(t)
x(t) (0, y), (") t 0, tF(x(
Din analiza matematica stim ca aria suprafetei de revolutie a curbei x([0,tF(x( ]) în jurul axei absciselor este :
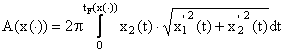(2)
astfel ca problema de geometrie enuntata initial se transforma în urmatoarea problema tipica de calcul variational (problema lui Plateau pentru suprafete de revolutie (problema variationala)).
Fiind dat y > 0 pentru fiecare
x0 = (,) R2
\ pentru care 
, în multimea Xcp(x0) a tuturor aplicatiilor de clasa C1 pe
portiuni
x( ) = (x1( ), x2( 0,tF(x( R2
cu proprietatile (1) sa se determine 
( Xcp(x0) care verifica C(( )) = min unde
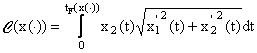(3)
Ca si în cazul problemei brachistochronei , daca notam x = u si definim multimile
XF X0: = (4)
obtinem urmatoarea
Problema
de control optimal fiind dat y > 0 care defineste multimile X0 si XF
din (4), pentru fiecare x0 X0 sa se determine 
( Ucp(x0), unde Ucp(x0) este multimea tuturor
functiilor continue pe portiuni u( ) = (u1( ), u2( [0, tF(x0, u( R pentru care
solutia x( x0, u( )) a problemey Cauchy
x' = u(t), x(0) = x0 (5)
verifica conditiile
x(tF(x0, u( )); x0, u( XF (6)
x(t; x0,u( X0, (") t [0, tF(x0, u( (7)
cu proprietatea 
, unde
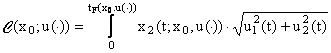dt (8)
b) Constructia sintezei optimale pentru problema suprafetei de revolutie de arie minima.
Problema lui Plateau pentru suprafete de revolutie este o problema Lagrange autonoma, (B) = (S, 0, f0( )), pe sistemul de comanda autonom S = (X0, XF, U( ), f( U )) definita de elementele
(9)
unde y > 0 este un numar real dat.
Pentru constructia sintezei optimale a acestei probleme aplicam
ALGORITMUL 2
PASUL I Se constata usor ca datele
problemei verifica ipotezele (I.1) si (I.2) deoarece X0, XF
, X0 XF = , XF 
si g( ): XF R
este i.s.c. Din (9) se observa ca f0( ):Y R2
si f( ):Y R2 sunt continue
(în raport cu ansamblul argumentelor) si local Lipchitz în raport cu
primul argument pe multimea deschisa Y R2 x R2 , Y0
= Graf(U( )) = X0 x R2 Y.
PASUL II. Conul cvasitangent la multimea X0 în punctual x X0, la dreapta, este dat de
, iar 
X = R2,
X = X0 XF = R x [0, astfel ca multifunctia 
Deoarece 
nu verifica
conditia de închidere 
= 
(x), (") x X0, alegem multifunctia U0(x)
= U(x), (") x X.
PASUL III. Deoarece problema (B) = (S, 0, f0( (M), construim problema Mayer, 
, asociata problemei (B) definita prin (9), pe
sistemul de comanda 
definita de
elementele
= X0 x R, 
= XF x R, 
, daca 
R2
(10)
Determinam hamiltonianul H( A R,
H(
)=
H(,u) = 0, (") () A = A 
, (11)
unde
(12)
Multifunctia
punctelor de minim 
H
este data de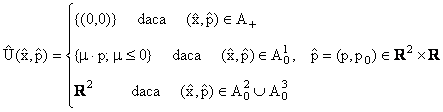 
(13)
PASUL V. Din
(10)-(12) rezulta ca 
si H( ) verifica Ipoteza (V.1) astfel
ca problema 
este stratificata
si deci în continuare se trece la RAMURA (S) a ALGORITMULUI 2 care începe
cu
PASUL VI(S). Pentru
determinarea multifunctiei 
P(R3),
, consideram
spatiul tangent la varietatea diferentiabila 
, în 
si deci
si
, 
, 
, 
si 
. Deci
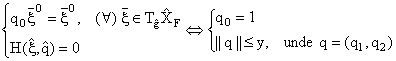
Am obtinut astfel ca valorile terminale ale variabilei adjuncte sunt
(14)
Analog, 
= , 
deoarece q0 =
0 si din 0 y ||q|| q = (0, 0), adica 
= (0, 0, 0) 
(
PASUL VII (S). Câmpul hamiltonian stratificat, 
( ), definit prin
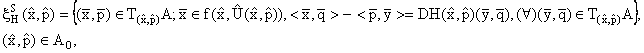se determina, tinându-se seama de (10)-(13),
astfel
(15)
Pentru fiecare 
determinam
solutiile 
ale incluziunii diferentiale 
. Se observa ca pentru fiecare asemenea solutie trebuie sa avem
daca 
(16)
si ca pentru 
nu exista nici o
solutie 
*( ) care sa verifice *(0) = (, ) x 
. Rezulta imediat ca
incluziunea diferentiala anterioara nu are solutii decât
pentru punctele multimii
(17)
si pentru fiecare asemenea solutie ( ) t1 < 0 astfel încât *(t) A
, (") t (t1, 0) si deci, în afara
relatiilor (16) componentele solutiei *( verifica
relatia
, (")t (t1, 0] daca 
. (18)
|
