Surse de informatie. Canale de transmisiune

Surse de informatie

1.1.1 Terminologie

Informatie Presupunem ca intr-o situatie oarecare pot avea loc N evenimete diferite, egal probabile, probabilitatea de realizare a unui eveniment A fiind p(A)=1/N. Odata ce unul din cele N evenimente au fost realizate se obtine o informatie. Aceasta informatie este cu atat mai mare cu cat 525f53f evenimentul este mai imprevizibil, respectiv cu cat probabilitatea sa este mai mica. Prin definitie informatia obtinuta este:

Ex 1. Aruncarea zarului.

Ex 2. Exista 12 monede din care una falsa ce poate fi mai usoara sau mai grea. Folosind o balanta egala sa se determine, utilizand notiunea de informatie, cate cantariri sunt necesare pentru a determina moneda falsa si sa se specifice daca este mai usoara sau mai grea.

A-    evenimentul determinarii monedei false;

B-    evenimentul determinarii daca moneda falsa este mai usoara sau mai grea;

C-    evenimentul compus A intersectat cu B.

p(A)= 1/12;   p(B)=1/2; p(C)=1/12*1/2= 1/24

i_C informatie necesara pentru a solva problema.

i_o = log₂ informatia furnizata de o cantarire (balata, la o cantarire, poate sa se incline spre dreapta, spre stanga sau sa nu se incline è 3 posibilitati).

k_min se afla punand conditia ca informatia furnizata de cantariri sa fie mai mare decat informatia necesara

k_min log₂3 ≥ log₂24 è k_min =3

Concluzii:

informatia, dupa definitia probabilitatii, ne da o masura calitativa asupra unui sistem, ne spune de cate cantariri avem nevoie nu spune cum se face masurarea cu balanta;

informatia este o masura cantitativa utila pentru analiza sistemelor de transmitere a informatiei.

1.1.2 Modelul unui sistem de transmisiune a informatiei

Cel mai simplu model al unui sistem de transmisiune a informatiei este:

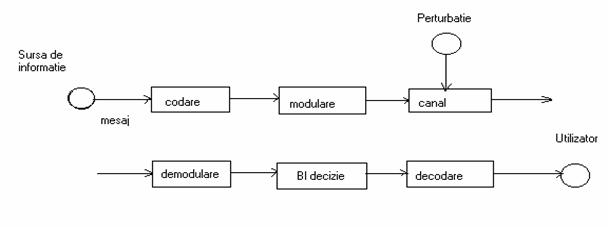
Sursa de informatie - un mecanism tehnic sau o procedura matematica care poate alege si emite un mesaj dintr-un ansamblu de mesaje posibile, alegerea facandu-se in mod aleator.

Sursa de informatie se caracterizeaza prin setul de mesaje posibil a fi selectate denumite simboluri sau litere.

Utilizator - destinatia finala la care trebuie sa ajunga mesajul transmis.

Canal - totalitatea mijloacelor destinate transmiterii mesajului prin mijloace intelegem atat aparatura cat si mediul prin care se poate transmite, si include toate sursele de perturbatii.

Modulare - transformarea unui mesaj intr-un semnal, cu scopul de a facilita transmisiunea printr-un canal dat sau de a realiza transmisiuni multiple prin acelasi mediu. Scopul secundar al modulatiei este de a mari eficienta transmisiunii prin micsorarea efectului perturbatiilor ce intervin in pocesul de transmisiune.

Demodulare - operatia inversa modularii.

Codare prelucrarea discreta a mesajului cu scopul maririi eficientei de transmisie. Uneori termenul de codare inglobeaza si modularea.

Decodare - operatia inversa codarii.

1.1.3 Cerintele unui sistem de transmisiune a informatiei

Sarcina unui sistem de transmisiune a informatiei este de a pune la dispozitia utilizatorului informatia generata de sursa, cu un grad de deteriorare specificat, admis.

In tehnicile de comunicatii se obisnuieste sa se introduca un criteriu de fidelitate, pentru aprecierea reproducerii semnalului generat de sursa la utilizator.

In sistemele de transmisiune analogica, criteriul de fidelitate ales este uneori eroarea medie patratica:

x(t) - mesaj transmis; y(t) - mesaj receptionat;

iar medierea se face in raport cu timpul; alteori se alege drept criteriu de fidelitate raportul   semnal/ zgomot.

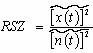
n(t) - zgomot perturbator

In sistemele de transmisie numerica criteriul de fidelitate il reprezinta probabilitatea receptionarii unui mesaj eronat, numita rata erorii (BER -Bit Error Rate).

1.1.4 Masura informatiei in cazul semnalelor discrete

Fie un experiment care are n realizari posibile pe care le organizam in spatiul esantioanelor.

X=

Fiecarui eveniment i se asociaza o probabilitate

P=   a.i.

Ansamblul [x,p] formeaza o sursa de informatie discreta.

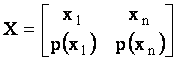
Masura incertitudinii asupra realizarii unui eveniment x_i este o functie de probabilitate apriorii de realizare a acestui eveniment F(p_i), unde: Pi = p(x_i); U(x_i) = F(p_i) si reprezinta incertitudinea initiala (apriori) asupra realizarii evenimentului x_i.

Cand evenimentul elementar x_i se realizeaza, aceasta incertitudine a fost inlaturata si se spune ca s-a obtinut o informatie i(x_i) asupra realizarii lui x_i. Acesta informatie poate fi definita prin :

- informatia obtinuta asupra lui x_i prin realizarea lui x_I;

- anularea incertitudinii asupra realizarii lui x_i dupa ce s-a realizat x_i

Functia F poate fi aleasa dintr-o clasa mare de functii care sa indeplineasca conditia de aditivitate: daca un eveniment x_i este format din 2 evenimente x_i1 si x_i2, x_I = x_i1 intersectat cu x_i2

i(x_i)=i(x_i1)+i(x_i2)   è F[p(x_i) =F[p(x_i1)]+F[p(x_i2)]

Fie cazul cel mai simplu al unei surse discrete formata din 2 evenimente:

S-a convenit sa se aleaga unitatea de informatie ca informatia ce se obtine prin alegerea la intamplare a unui eveniment din doua evenimente egale probabile:

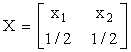
1.1.5 Tipuri de surse de informatie

Surse discrete - care debiteaza mesaje in forma discreta (de ex. succesiunea de impulsuri)

Def: X_i - simbol sau litera este elementul fundamental ireductibil care contine   informatie, respectiv o realizare particulara a sursei de informatie.

- alfabet, totalitatea simbolurilor;

Cuvant - o succesiune finita de simboluri binare;

Limba - totalitatea cuvintelor formate cu un anumit alfabet;

Codare sau cifrare - se stabileste o corespontenta intre o limba si alta limba;

Decodare sau decifrare - operatia inversa codarii;

Sursa discreta fara memorie - sursa la care probabilitatea de aparitie a unui simbol nu depinde de simbolurile precedente:

Sursa discreta cu memorie -sursa la care probabilitatea de aparitie a unui simbol depinde de simbolul precedent sau de un sir de simboluri anterioare, daca sursa are o memorie mai mare.

Sursa stationara -sursa la care probabilitatile diferitelor simboluri nu depind de originea timpului in care incepe observarea acesteia.

Sursa ergodica - este sursa pentru care frecventele de aparitie a diferitelor simboluri obtinute prin observarea unei secvente particulare de simboluri emise de sursa tind catre probabilitatile acestora p₁,.,p_n.

Sursa discreta fara constrangeri - sursa stationara care nu are memorie, adica sursa la care dupa un simbol poate urma orice alt simbol cu aceeasi probabilitate.

Sursa discreta cu constrangeri fixe - este sursa la care unele simboluri pot fi folosite numai in conditii bine precizate.

1.1.6 Parametrii surselor de informatie

Entropia H(X) este incertitudinea medie apriori asupra evenimentelor sursei X sau informatia proprie medie pe simbol a respectivei surse.

Proprietatile entropiei:

Continuitatea - H(X) este o functie continua in raport cu p_i Є [0,1];

Simetria - simetrica in raport cu p_I;

Aditivitatea - aditivitatea informatiei proprie;

Entropia are maximul pentru P₁=P₂=.=P_n;

Exemplificam pentru cazul unei surse binare:

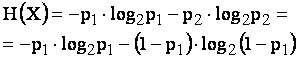
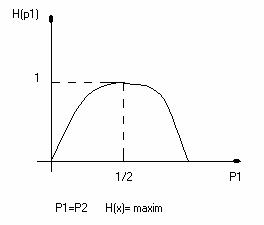
Debitul de informatie

In unele situatii este util ca notiunea de informatie sa fie legata de timp. In acest caz, se defineste debitul de informatie ca raportul intre entropia sursei si timpul mediu de emisie a unui simbol al sursei.

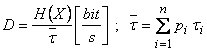
Redundanta unei surse

Pentru a indica cat de mult se indeparteaza entropia unei surse de la valoarea ei maxima posibila, se defineste redundanta ca fiind diferenta intre valoarea maxima a entropiei sursei si valoarea ei reala.

, unde:

Eficienta sursei

Eficienta unei surse se defineste ca fiind:

Redundanta relativa

Este redundanta raportata la entropia maxima:

1.2 Canale discrete

1.2.1 Terminologie

Intre sursa de informatie si utilizator, exista un mediu prin care trebuiesc transmise informatiile, care se numeste canal.

Canalul ca si model matematic, stabileste o transformare de la spatiul simbolurilor de intrare , la spatiul simbolurilor de iesire .

Canalul se numeste discret, daca atat spatiul de intrare, cat si cel de iesire, sunt discrete. Vom analiza un astfel de canal discret.

Daca nu se face nici o ipoteza asupra independentei sau dependentei elementelor x_i si y_j , avem matricea de probabilitati sau matricea de transfer a canalului:

Aceasta matrice, are proprietatea ca:

Canalul discret poate fi definit de trei campuri carora le corespund trei entropii:

campul de intrare H(X);

campul de iesire H(Y);

campul reunit intrare iesire H(X,Y).

Expresiile acestor entropii sunt:

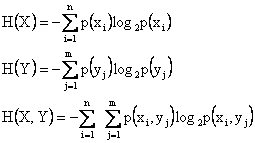
Echivocatia

Daca, campul de evenimente de la iesirea din canal este cunoscut, datorita efectelor perturbatiilor ramane totusi o oarecare incertitudine asupra campului de la intrare.

Valoarea medie a acestor incertitudini, entropia campului X conditionat de campul Y, se noteaza cu H(X/Y) si se numeste echivocatie. Reprezinta masura echivocului, a incertitudinii asupra campului de intrare, cand se cunoaste campul de iesire Y.

x₁ o   oy₁

x_no   y_m

Daca la iesirea din canal, apare simbolul y_j, exista o incertitudine asupra simbolului care a fost de fapt emis. Acesta poate sa fie oricare dintre x₁,...x_n. Incertitudinea asupra emiterii simbolului x₁ daca s-a receptionat y_j, este:

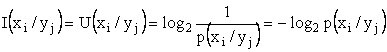
Valoarea medie a acestei incertitudini este:

Daca facem valoarea medie pentru toate valorile posibile ale lui y_j este:

Eroarea medie. In mod analog, se poate determina entropia campului de iesire, daca se cunoaste campul de la intrare.

Eroarea medie, este o masura a incertitudinii campului de la iesire cand se cunoaste campul de la intrare

Daca, canalul nu are perturbatii atunci:

Daca, canalul are perturbatii foarte puternice, atunci:

Pentru determinarea entropiilor conditionate este necesar sa cunoastem matricile conditionate de transfer ale canalului.

si

Transinformatia

Daca consideram iesirea canalului si observam la un moment dat evenimentul y_j, masura incertitudinii, daca la intrarea acestuia s-a introdus x_i, este:

Informatia obtinuta la iesirea canalului asupra realizarii lui x_i, cand a iesit y_j, este egala cu scaderea din incertitudinea apriori despre realizarea lui x_i a incertitudinii aposteriori   , adica:

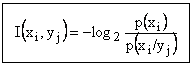
sau