TRANSFORMATOARE ELECTRICE

TRANSFORMATOARE ELECTRICE

Transformatoarele electrice sunt dispozitive electromagnetice statice de curent alternativ, constituite în principal din doua sau mai multe înfasurari cuplate magnetic, a caror functie de utilizare consta în modificarea parametrilor tensiune si curent ai energiei electrice. În cazul aplicatiilor de frecventa redusa, sub 10 kHz, cuplajul magnetic dintre înfasurari se asigura prin intermediul unui miez feromagnetic.

Primul transformator cu miez magnetic si doua înfasurari a fost construit de    M. Faraday n 1831, în scopul evidentierii experimentale a fenomenului inductiei electromagnetice.

3.1. ELEMENTE CONSTRUCTIVE. PRINCIPIUL DE FUNCŢIONARE.

MĂRIMI NOMINALE. SIMBOLIZARE. INDUCTIVITĂŢI

3.1.1. Elemente constructive

Fie ca sunt mono - , tri - , sau în general multifazate, transformatoarele sunt constituite în calitate de subansamble active din doua sau mai multe circuite electrice - înfasurari, dispuse în jurul unui circuit magnetic închis, denumit miez magnetic

Miezul magnetic poate fi de tip lamelat, constituit din tole de otel electrotehnic, izolate electric între ele, sau de tip masiv, din ferite magnetic moi. În mod uzual, pentru aplicatii la 50 Hz tolele au grosimea de 0,35 mm pe masura ce frecventa creste, asigurarea unui nivel rezonabil al pierderilor de putere activa în miez impune utilizarea unor tole de grosime din ce în ce mai redusa. Sub denumirea de otel electrotehnic se întelege un aliaj fier siliciu, caracterizat prin pierderi specifice în curent alternativ cu atât mai reduse cu cât continutul de siliciu este mai ridicat. Având în vedere ca orientarea fluxului magnetic este una invariabila în diversele zone ale miezului magnetic, se utilizeaza în special în cazul transformatoarelor de putere medie si mare tole cu proprietati anizotrope, cu pierderi mai mici atunci când fluxul magnetic este orientat dupa directia de usoara magnetizare.

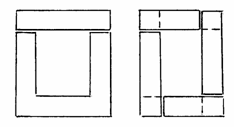
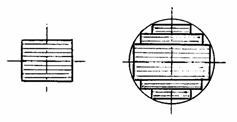
În cazuri cu totul speciale miezul magnetic se construieste monobloc, de exemplu sub forma toroidala. În general, montarea si demontarea facila a înfasurarilor, impune ca miezul sa se constituie din subansamble separate, cele în jurul carora se plasează 454i88e ; bobinele fiind denumite coloane, iar celelalte subansamble de legatura între coloane, denumite juguri. Desi solutia cea mai simpla referitoare la forma sectiunii transversale a miezului magnetic este aceea patrata sau dreptunghiulara, fig. 3.1 a), se prefera în cazul transformatoarelor de puteri medii si mari > 1 kVA, la 50 Hz) realizarea în trepte a coloanelor în principal, dar si a jugurilor , fig. 3.1 b). Aceasta solutie este în principal impusa de structura înfasurarilor, mult mai comod a fi realizate atunci când spirele sunt circulare decât în cazul spirelor dreptunghiulare.

a) b) a) b)

Fig. 3.1 Fig. 3.2

Îmbinarea dintre coloane si juguri poate fi prin suprapunere, fig. 3.2 a) sau prin ntretesere, fig. 3.2 b). În primul caz, rezulta în lungul liniilor de câmp magnetic un întrefier net de 0,1 ..1 mm, zona în care, pentru a evita producerea unor pierderi suplimentare, este necesara prevederea unei izolatii electrice. În cazul îmbinarii prin întretesere a jugului cu coloana, în zonele de colt, fig. 3.2 b alterneaza tole ale coloanei, respectiv jugului. Câmpul magnetic de la o tola a coloanei la tola corespondenta a jugului se închide preponderent lateral, prin izolatia dintre tole rezulta astfel un întrefier echivalent mult mai mic, de numai 0,02..0,06 mm.

Miezul magnetic poate fi de tipul cu coloane, fig. 3.3. a), sau de tipul în manta, fig. 3.3. b. În exemplul pentru transformator monofazat din figura 3.3. avem de-a face cu o solutie cu doua coloane [cazul a)], respectiv cu o coloana [cazul b)].

Înfasurarile se construiesc din conductor izolat de cupru sau aluminiu. Luând ca exemplu tipic transformatorul cu doua înfasurari, se folosesc în mod uzual denumirile de înfasurare primara, respectiv secundara, dupa sensul de transfer al energiei electrice, sau înfasurare de înalta tensiune î.t.), respectiv joasa tensiune (j.t. dupa valorile tensiunilor nominale ale celor doua înfasurari. Se convine sa se noteze cu indicele 1 toate marimile caracteristice înfasurarii primare si cu indicele 2 marimile asociate înfasurarii secundare.

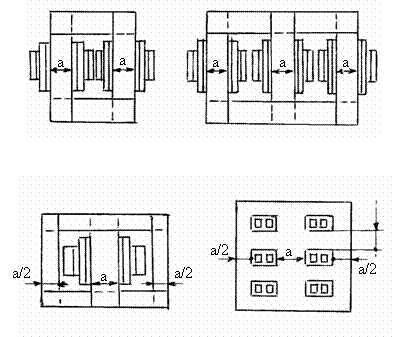
Înfasurarile cilindrice concentrice, fig. 3.4 a), b) sunt asezate suprapus pe

Fig. 3.3 aceeasi coloana, de regula

înfasurarea de joasa tensiune lânga miez, iar înfasurarea de înalta tensiune în exterior. Structura din figura 3.4 b), în care una dintre înfasurari este intercalata între doua sectiuni ale celeilalte, asigura un cuplaj magnetic mai bun al celor doua înfasurari, respectiv un flux de dispersie mai redus.

a) b) c)

Fig. 3.4

Plasarea înfasurarilor primara si secundara pe coloane diferite reduce cuplajul magnetic al acestora, lucru dorit în cazul unor transformatoare destinate sudurii electrice.

În sistemul înfasurari în galeti alternati, fig. 3.4. c), în lungul coloanei se succed bobine (galeti) ale înfasurarii primare, respectiv înfasurarii secundare. Se plaseaza de regula spre juguri galeti ai înfasurarii de joasa tensiune. Cuplajul magnetic dintre înfasurari este cu atât mai bun cu cât numarul de galeti este mai mare.

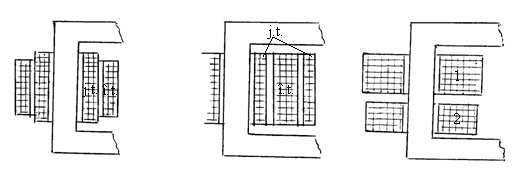
Înfasurarile cu numar mare de spire si valori reduse ale curentului, care nu necesita mai multe conductoare în paralel, se executa sub forma de înfasurari cilindrice stratificate, sau înfasurari cu galeti separati, fig. 3.5. a , b). Atunci când valoarea ridicata a curentului impune utilizarea mai multor conductoare în paralel, pentru ca în fiecare conductor elementar refularea curentului sa fie neglijabila, în executia înfasurarilor cilindrice elicoidale sau în galeti se efectueaza transpozitii ale conductoarelor în paralel; aceasta solutie tehnica face ca curentul total sa se distribuie uniform pe toate caile de curent în paralel, fig. 3.6.

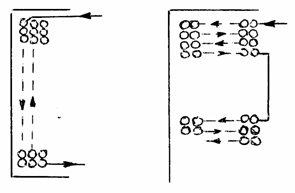
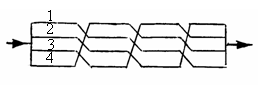
Fig. 3.6

Functionarea transformatoarelor este

a) b) însotita în mod inevitabil de dezvoltarea

Fig. 3.5 unei puteri active în miezul magnetic

(efectul curentilor turbionari indusi în tole si al histerezisului magnetic si în înfasurari (efectul Joule al curentilor). Asigurarea regimului termic în concordanta cu stabilitatea termica a materialelor izolante utilizate presupune evacuarea acestor pierderi. Se diferentiaza în acest sens transformatoare uscate si transformatoare în ulei. Cea de-a doua solutie constructiva are înca o pondere importanta, deoarece uleiul îndeplineste atât rol de mediu de racire cât si pe acela de izolant electric. Eficienta transferului termic prin intermediul mediului lichid care este uleiul este sensibil superioara transferului prin convectia aerului. Constructia si întretinere transformatoarelor în ulei ridica probleme mai complexe decât transformatoarele uscate; aceasta explica evolutia variantei uscate pentru puteri medii si mici, care este sustinuta si de dezvoltarea unor materiale si solutii constructive eficiente, cum ar fi de exemplu înglobarea înfasurarilor în rasini sintetice cu stabilitate termica ridicata.

3.1.2. Principiul de functionare, simbolizare, marimi nominale

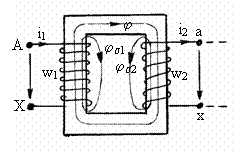
Transformatorul monofazat reprezentat în figura 3.7 este alimentat cu tensiunea u₁ , ce se aplica înfasurarii primare, care are w₁ spire si este parcursa de curentul i₁. Parametri corespondenti ai înfasurarii secundare sunt tensiunea la borne u₂ , numarul de spire w₂ si curentul i₂ , debitat în cazul functionarii în sarcina.

Fig. 3.7

Cuplajul magnetic al celor doua înfasurari nefiind niciodata perfect, rezulta ca fluxul magnetic ce strabate fiecare înfasurare este constituit din componenta comuna, fluxul principal din miez j si fluxurile specifice de scapari j_s si j_s . În concordanta cu sensurile curentilor prin cele doua înfasurari, rezulta ca fluxurile magnetice fasciculare corespondente au expresiile

Atunci când înfasurarea secundara nu debiteaza curent, transformatorul absoarbe curentul de mers în gol i₁₀, a carui valoare este mult mai mica decât valoarea curentului primar la functionarea transformatorului în regimul de sarcina nominala (când i₂ = i_2n si i₁ = i_1n) ; în mod uzual, i₁₀ ( 2.4 %) i_1n. Aceasta se explica prin faptul ca transformatoarele se dimensioneaza astfel ca starea de magnetizare a miezului magnetic sa corespunda cotului curbei de magnetizare B(H), ceea ce înseamna o valoare relativ ridicata a permeabilitatii magnetice, respectiv o valoare considerabila a inductivitatii în raport cu bornele de alimentare la functionarea în gol.

Puterea activa absorbita la functionarea în gol are valori reduse datorita aportului nesemnificativ al pierderilor Joule în înfasurarea primara. Pe de alta parte, pierderile în miezul magnetic au valorii reduse în raport cu puterea nominala, deoarece acesta este conceput pentru a îndeplini functia de circuit magnetic. Grosimea tolei elementare se alege întotdeauna astfel încât adâncimea de patrundere a câmpului alternativ corespunzatoare frecventei de lucru sa fie mult mai mare decât aceasta, ceea ce are ca rezultat o valoare nesemnificativa a curentilor indusi în tole, respectiv a pierderilor prin curenti turbionari.

Ecuatiile de tensiuni ale celor doua înfasurari la functionarea în gol al transformatorului (i₁₀ << i_1n , i₂ = 0, j_s = 0) sunt:

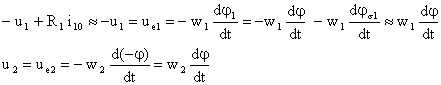
S-a tinut cont în prima relatie de proprietatile R₁i₁₀ << u₁ , unde R₁ este rezistenta înfasurarii primare, si j_s << j Prin raportarea celor doua relatii se obtine

relatie ce exprima proprietatea ca raportul tensiunilor primara si secundara în regimul de gol al transformatorului, denumit raport de transformare, este egal cu raportul numerelor de spire corespunzatoare.

Atunci când transformatorul functioneaza în sarcina, i₂ 0 , solenatia de magnetizare a miezului are expresia

Aproximatiile R₁i₁ << u₁ si j_s << j ramân valabile chiar si pentru functionarea la sarcina nominala, ceea ce însemna u₁ = w₁ , respectiv ca fluxul magnetic principal j nu este practic influentat de regimul de sarcina drept consecinta solenatia de magnetizare poate fi exprimata si în functie de curentul de mers în gol, respectiv q_m w₁i₁₀. Cum solenatia de magnetizare în gol, w₁i₁₀ , este mult mai mica decât solenatia înfasurarii primare în sarcina, w₁ i₁ , rezulta

w₁ i₁ - w₂ i₂

respectiv,

Asadar, la functionarea în sarcina, raportul curentilor prin înfasurarile primara si secundara este practic egal cu inversul raportului de transformare.

Într un regim de sarcina oarecare, transformatorul absoarbe prin înfasurarea primara puterea instantanee p₁ u₁ i₁ si debiteaza pe sarcina puterea p₂ u₂ i₂. Conform relatiilor de mai sus, rezulta ca în aproximatia neglijarii pierderilor de putere activa în miez si înfasurari si a puterii reactive corespunzatoare fluxurilor de scapari, rezulta

p₁ u₁ i₁ = u₂ i₂ = p₂

Prin urmare, transformatorul electric converteste valoarea u₁ a tensiunii de alimentare în valoarea u₂ , convenabila sarcinii, absorbind din reteaua de alimentare puterea solicitata de receptor, daca se face abstractie de pierderi.

În cazul particular al functionarii în regim armonic permanent, se scrie

ceea ce înseamna ca tensiunile si curentii primari, respectiv secundari sunt, în aproximatiile precizate mai sus, în faza sau în opozitie de faza. În aproximatia neglijarii pierderilor de putere activa se poate scrie egalitatea

ceea ce înseamna ca factorul de putere al ansamblului transformator sarcina este egal cu factorul de putere al sarcinii, cos j = cos j

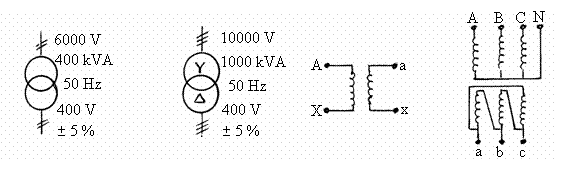Semnele conventionale pentru simbolizarea transformatoarelor în schemele electrice sunt cele din figura 3.8.

Fig. 3.8

Serviciul nominal de functionare al unui transformator, stabilit prin tema de proiectare, este acela pentru care temperatura maxima în diferite zone ale acestuia nu depaseste limitele impuse de clasa de izolatie a materialelor utilizate. Regimul nominal de functionare, caracteristic serviciului nominal, se defineste prin urmatoarele date nominale:

puterea nominala S_n este puterea aparenta debitata prin bornele secundare, pentru care nu sunt depasite limitele admisibile ale încalzirii, în conditiile alimentarii la parametrii nominali (tensiune si frecventa);

tensiunea nominala primara U_1n este tensiunea ce trebuie aplicata înfasurarii primare în regimul nominal de functionare al transformatorului;

tensiunea nominala secundara U_2n este în cazul transformatoarele peste 10 kVA tensiunea la bornele înfasurarii secundare atunci cand transformatorul functioneaza în gol, fiind alimentat cu tensiunea nominala U_1n ; în cazul transformatoarelor cu puteri sub 10 kVA, este tensiunea la bornele înfasurarii secundare corespunzatoare regimului de sarcina în care transformatorul debiteaza curentul secundar nominal;

raportul nominal de transformare este raportul dintre tensiunile nominala primara si secundara la mersul în gol;

curentii nominali primar I_1n si secundar I_2n sunt curentii de linie evaluati pe baza puterii si tensiunii nominale;

tensiunea de scurtcircuit nominala u_sc , exprimata în procente fata de tensiunea U_1n , este tensiunea ce trebuie aplicata înfasurarii de înalta tensiune pentru a fi parcursa de curentul nominal, atunci când înfasurarea de joasa tensiune este scurtcircuitata;

frecventa nominala poate fi frecventa industriala, 50 Hz, sau o alta valoare specificata ca data de baza a transformatorului.

3.1.3. Inductivitati ale circuitelor cuplate magnetic, cu aplicatie la

transformatoare

Doua circuite electrice sunt cuplate magnetic în cazul în care câmpul magnetic creat de curentul ce parcurge unul din circuite se închide partial, sau la limita în totalitate, prin celalalt circuit. Cuplajul magnetic al circuitelor se caracterizeaza prin anumite marimi denumite inductivitati, respectiv coeficienti de dispersie.

a) Inductivitati proprii si inductivitati mutuale. Curentul i₁ ce parcurge bobina 1-1', fig. 3.9, determina o structura de câmp magnetic care asigura fluxul magnetic w₁j prin bobina 1-1' si fluxul w₁j prin bobina 2-2'. Marimile j si j se numesc fluxuri magnetice fasciculare, cu referire la una din cele w_{1 ,} respectiv w₂ spire ale bobinelor respective.

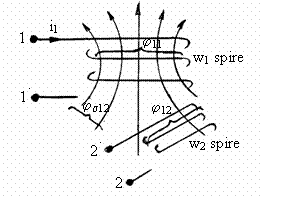
Marimea

este inductivitatea proprie a bobinei 1 , iar

este inductivitatea mutuala dintre bobinele

Fig. 3.9. 1 si 2. În mod asemanator se definesc

inductivitatea proprie a bobinei , respectiv inductivitatea mutuala dintre bobinele 2 si 1,

si

În cazul structurilor magnetic liniare si electric filiforme cele doua inductivitati mutuale au aceasi valoare, L₂₁ L₁₂ , denumita inductivitatea mutuala a celor doua bobine.

Inductivitatea mutuala a doua bobine depinde de numerele de spire ale celor doua bobine, al caror cuplaj magnetic îl caracterizeaza

b) Inductivitati utile si inductivitati de dispersie. Fluxul magnetic fascicular j al bobinei se exprima ca suma dintre fluxul fascicular prin bobina si un flux fascicular j_s , denumit flux de scapari

Pentru o caracterizare mai riguroasa a cuplajului celor doua bobine vom denumi fluxul j flux util al cuplajului, j_u12. Exprimând fluxul j ca suma a fluxurilor util si de scapari,

pot fi definite

inductivitatea utila a bobinei 1 în raport cu bobina 2:

inductivitatea de dispersie, sau de scapari, a bobinei 1 în raport cu bobina 2

În mod analog, scriind

,

se definesc inductivitatile utile si de dispersie ale bobinei 2 în raport cu bobina 1,

,

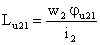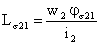
Inductivitatea utila si inductivitatea de dispersie ale unei bobine în raport cu alta depind ambele de numarul de spire al bobinei la care se refera.

Inductivitatilor utile si de dispersie se exprima în functie de inductivitatile proprii si mutuale prin relatiile

Pe baza acestor relatii rezulta si egalitatile

L₁₁ = L_u12 + L_s L₂₂ = L_u21 + L_s ; .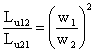

Exemplu: Fie doua bobine având w₁ 100 spire si w₂ = 10 spire, caracterizate prin urmatoarele valori ale inductivitatilor proprii si mutuale: L₁₁ = 1256 mH ; L₂₂ = 12,56 mH ; L₁₂ = L₂₁ = 113 mH.

Coeficientul de cuplaj magnetic al acestor bobine are valoarea:

Inductivitatile utila si de dispersie au valorile:

bobina 1 L_u12 1130 mH L_s = 1256 - 1130 = 126 mH ;

- bobina 2 L_u21 = 11,3 mH ; L_s = 12,56 - 11,3 = 1,26 mH

Observatii

1) Un cuplaj perfect k nu ar apare ca evident la simpla observare a valorilor inductivitatilor proprii si mutuale, în timp ce pentru un astfel de cuplaj inductivitatile de scapari sunt nule, L_s L_s

2) Cu cât inductivitatile de dispersie au valori mai reduse în raport cu inductivitatile utile, cu atât cuplajul magnetic este mai bun. Pentru L_s L_u12 rezulta ca bobinele 1 si 2 nu sunt cuplate magnetic.

având w₁ spire). Circuitul magnetic din figura 3.10 al unui transformator este constituit din trei zone distincte, caracterizate prin valori constante ale inductiei magnetice

- doua coloane de lungime l_c si sectiune S_c

- doua juguri de lungime l_j si sectiune S_j ;

- o zona modelând un întrefier echivalent, de lungime d si sectiune S_d

Relatiile

si

Fig. 3.10

exprima legea circuitului magnetic si legea fluxului magnetic. Folosind dependentele , si dintre inductii si intensitatile câmpului magnetic, se deduce expresia inductiei în coloane:

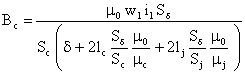
Inductivitatea utila are expresia

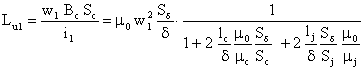
Se observa urmatoarele proprietati

- inductivitatea L_u este proportionala cu patratul numarului de spire

- inductivitatea L_u este proportionala cu aria sectiunii transversale

- inductivitatea L_u este invers proportionala cu întrefierul echivalent d

- inductivitatea utila depinde de starea de magnetizare a miezului ;

În cazul ideal, când si , rezulta expresia simplificata

,

caz care ar corespunde de unui miez magnetic de permeabilitate infinita, nu exista linii închise ale intensitatii câmpului magnetic, care sa înconjoare ambele înfasurari. Ca urmare, câmpul magnetic creat de cele doua înfasurari are caracterul exclusiv al unui câmp magnetic de dispersie.

Fie h_b dimensiunea axiala a bobinelor, considerate a avea aceeasi

Fig. 3.11 lungime. În aplicarea legii circuitului

magnetic pe conturul închis al unei linii

de câmp magnetic, contributia zonei din miezul magnetic este neglijabila. Se face ipoteza simplificatoare ca liniile câmpului magnetic în fereastra transformatorului sunt verticale (H_y 0, H_x = 0) si vom echivala integrala de-a lungul unei linii de câmp reale cu produsul , unde H_y are variatia din figura 3.11 pe latimea ferestrei, iar k_R este factorul de corectie Rogowsky. Conform acestei ipoteze:

, pentru x [0, a₁]

, pentru x [a₁, a₁ + a₁₂]

, pentru x [a₁ + a₁₂ , a₁ + a₁₂ + a₂]

Calculul inductivitatii de dispersie al bobinei 1 presupune evaluarea fluxului magnetic total de dispersie F_s care înlantuie spirele acesteia. Se considera bobina desfasurata, de lungime pD_m , asezata în fereastra transformatorului se admite de asemenea ca suprafata cilindrica reala de diametru D_m , fig. 3.11, separa liniile de câmp ce se închid printr-o bobina, respectiv prin cealalta. Fluxul magnetic de dispersie al bobinei 1 se evalueaza cu relatia

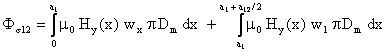
Fluxul magnetic elementar m H_y p D_m dx în domeniul x [0, a₁] înlantuie numarul de spirele . Se obtine

respectiv expresia inductivitatii de dispersie a înfasurarii 1

În mod analog se calculeaza inductivitatea de dispersie a înfasurarii 2

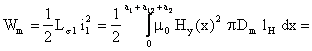
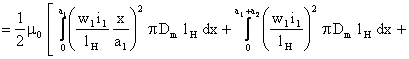
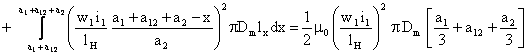
Rezulta

Inductivitatea totala de dispersie în raport cu bornele înfasurarii primare 1 depinde de numarul de spire w₁ al acestei înfasurari, de factorul de geometrie si de latimea echivalenta a canalului de scapari (de dispersie ), .

Este usor de verificat ca daca înfasurarea 2 se sectioneaza în doua bobine de latime a₂ 2 , care se plaseaza de o parte si de alta a înfasurari 1, spatiul dintre bobine ramânând a₁₂ , atunci inductivitatea totala de dispersie are expresia

mai putin de jumatate în raport cu valoarea anterioara. Prin urmare, intercalarea înfasurarilor primare si secundare ale unui transformator face sa scada inductivitatea totala de dispersie , altfel spus îmbunatateste cuplajul magnetic al celor doua înfasurari.

3.2. TEORIA FIZICĂ A TRANSFORMATORULUI

Teoria fizica a transformatorului face apel la fluxurile, respectiv inductivitatile proprii si mutuale.

3.2.1. Ecuatiile de functionare în regim tranzitoriu

Se considera miezul magnetic liniar, fara pierderi, înfasurarea primara este receptor de energie electrica, iar cea secundara genereaza energie electrica pe o sarcina R, L, C serie, fig. 3.12. Aplicând legea inductiei electromagnetice pentru cele doua circuite ale transformatorului se obtine

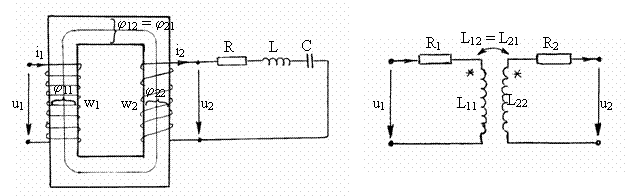
Fig. 3.12 Fig. 3.13

Schema echivalenta corespunzatoare acestor ecuatii este aceea din figura 3.13. Adaugând ecuatia circuitului receptor:

,

rezulta un sistem cu necunoscutele u₂, i₁ si i₂, presupunând ca tensiunea de alimentare u₁ si toti parametrii au valori cunoscute.

În conditiile cunoasterii conditiilor initiale, la t 0 , referitoare la necunoscutele sistemului, pot fi obtinute pe cale analitica (uneori) sau numerica (practic întotdeauna solutiile u₂(t), i₁(t) si i₂(t).

Exemplu regimul tranzitoriu la aplicarea unei trepte de tensiune în primar U, cu secundarul în gol, i₂

Pentru t > 0, curentul instantaneu i₁ absorbit de primar satisface ecuatia

Cu conditia initiala i(0) = 0, rezulta solutia:

unde t = L₁₁ / R₁ este constanta de timp a înfasurarii primare.

3.2.2. Ecuatiile, schema echivalenta si diagrama de fazori în regimul armonic

permanent

Daca tensiunea de alimentare are expresia instantanee , prin aplicarea reprezentarii în complex simplificat rezulta

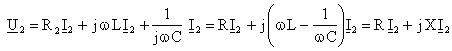
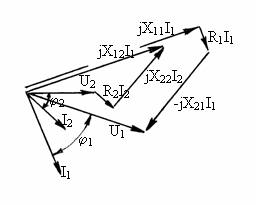Pornind de la fazorul U₂ al tensiunii secundare si considerând fazorul I₂ ca parametru, rezulta diagrama de fazori din figura 3.14; constructia diagramei de fazori urmeaza succesiunea indicata prin cifrele de la 1 la 10. Pornind de la ansamblul de valori caracteristice circuitului secundar, U₂, I₂, j , se obtine ca rezultat final al constructiei diagramei de fazori valorile caracteristice primarului, U₁, I₁, j

Pe baza ultimelor doua ecuatii ale sistemului anterior se obtine relatia

Fie coeficientul de cuplaj al curentilor; se observa usor ca . Cu aceasta notatie

Fig. 3.14

rezulta

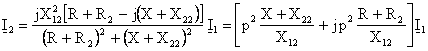
Înlocuind în prima ecuatie se obtine

Sistemul transformator - sarcina se caracterizeaza în raport cu sursa de alimentare prin parametrii echivalenti R_e si X_e , care depind atât de parametrii sarcinii cât si de parametrii transformatorului.

În cazul limita al functionarii în gol, I₂ = 0, p = 0 rezulta

Curentul de mers în gol I₁₀ este practic limitat de reactanta proprie a înfasurarii primare X₁₁, a carei valoare este mult superioara rezistentei R₁ .

În cazul scurtcircuitarii bornelor secundare, R = 0 , L = 0, C = , rezulta . În cazul unui cuplaj magnetic bun al celor doua înfasurari este valabila relatia X₁₂²­ X₁₁ X₂₂, ceea ce conduce la ­­­. Prin urmare, parametrul rezistenta echivalenta de scurtcircuit în raport cu bornele primare are expresia

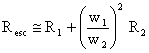
Parametrul reactanta echivalenta de scurtcircuit în raport cu aceleasi borne primare are expresia

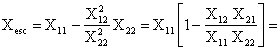
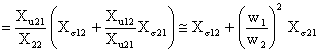
În succesiunea anterioara s-a neglijat produsul X_s X_s în raport cu ceilalti doi termeni si s a considerat ca X_u21 X₂₂ .

3.3. TEORIA TEHNICĂ A TRANSFORMATORULUI

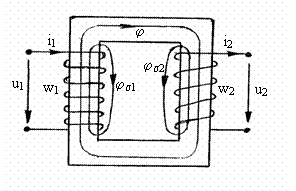Teoria tehnica a transformatorului face apel la inductivitatile utile si de dispersie, considera nelinearitatea magnetica a miezului si pierderile în acesta. Se adopta aceleasi conventii de semne pentru tensiuni si curenti ca si în capitolul anterior, iar câmpului magnetic i se asociaza fluxul magnetic principal în miez j si fluxurile magnetic de dispersie al înfasurarii primare j_s si al înfasurarii secundare j_s , ambele în raport cu cealalta înfasurare, fig. 3.15.

Fluxul magnetic principal j este produs de solenatia magnetica rezultanta, denumita solenatie de magnetizare

Ecuatiile de tensiuni ale celor doua circuite sunt

Fig. 3.15

Cum câmpul magnetic de dispersie se închide în buna masura prin aer, dependenta dintre fluxurile j_s j_s si curentii corespunzatori este practic liniara, ceea ce permite definirea parametrilor inductivitati de dispersie ai celor doua înfasurari

Adaugând la ecuatiile de mai sus ecuatia receptorului, se obtine sistemul

Acest ansamblu de ecuatii formeaza un sistem neliniar, cu necunoscutele i₁, u₂, i₂, j neliniaritatea este datorata ultimei ecuatii, care reprezinta caracteristica magnetica a miezului.

În ipoteza unei caracteristici magnetice liniare a miezului, definind curentul de magnetizare i_m prin relatia , se poate asocia fluxului magnetic principal j inductivitatea utila L_u12 definita prin relatia

Practic oricare ar fi regimul de sarcina , de la gol pâna la sarcina nominala, caderile de tensiune R₁i₁ si au valori atât de mici în raport cu tensiunea de alimentare încât se poate admite ca

Aceasta relatie evidentiaza proprietatea ca fluxul magnetic principal depinde de tensiunea de alimentare si variaza relativ putin în raport cu regimul de încarcare în sarcina. Rezulta astfel ca daca tensiunea u₁ este armonica, cu buna aproximatie si fluxul j are o variatie armonica în timp.

3.3.1. Ecuatiile de functionare în regim armonic, schema echivalenta si

diagrama de fazori

Fie expresia instantanee a tensiunii de alimentare. Se considera ca miezul este magnetic liniar. Prin aplicarea reprezentarii în complex simplificat ecuatiile de mai sus devin

S-au notat cu U_e1, U_e2 tensiunile electromotoare induse în înfasurari de fluxul principal F modulul marimii complexe F fiind egal cu amplitudinea fluxului magnetic principal, rezulta expresiile

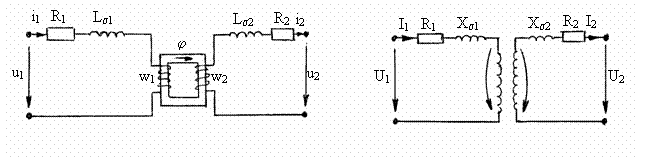
Ecuatiilor în instantaneu si cele în complex asociaza transformatorului schemele echivalente din figurile 3.16 si 3.17.

Fig. 3.16 Fig. 3.17

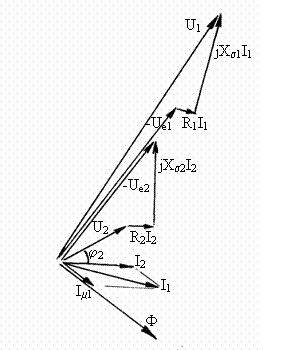
Pornind de la fazorul U₂ al tensiunii secundare si considerând curentul de sarcina I₂ ca parametru, rezulta diagrama de fazori din figura 3.18, care determina succesiv tensiunile electromotoare U_e1, U_e2, fluxul F, curentul de magnetizare I_m, curentul I₁ si tensiunea de alimentare U₁. Curentul I_m are expresia

3.3.2. Raportarea circuitului secundar la primar

Observând ca:

Fig. 3.18 se poate scrie

S-au folosit notatiile

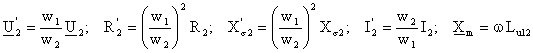
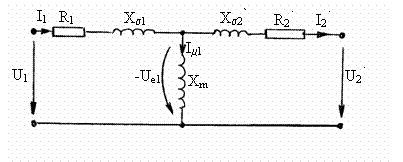care definesc respectiv tensiunea si curentul secundar raportate la primar, parametrii rezistenta si reactanta de scapari ai înfasurarii secundare raportati la primar si reactanta de magnetizare reactanta utila) a transformatorului. Cu acestea, schema echivalenta a transformatorului raportat are structura din figura 3.19. O diagrama de fazori asemanatoare celei din figura 3.18 poate fi asociata sistemului de ecuatii al transformatorului raportat.

Fig. 3.19

3.3.3. Considerarea pierderilor de putere activa în miezul magnetic

Fenomenul de histerezis determina, în conditiile unei magnetizari alternative, cum este cazul miezului transformatorului, transformarea ireversibila a unei parti a energiei electromagnetice în caldura. Conform relatiei lui Steinmetz, pierderile specifice prin histerezis depind de inductia magnetica locala B si de frecventa câmpului prin relatia

Aceste pierderi pot fi exprimate pentru valorile uzuale ale inductiei magnetice în dispozitivele electrotehnice si în functie de patratul inductiei prin relatia mai potrivita

O alta componenta a puterii active dezvoltate într un miez magnetic în alternativ este rezultatul efectului Joule al curentilor turbionari indusi. Se demonstreaza ca în conditiile prezentei unei tole de grosime D, dintr un material cu rezistivitatea r si densitatea g, într-un câmp magnetic omogen, orientat în lungul tolei, densitatea de masa a puterii induse are expresia

Prin urmare, pierderile specifice de putere în miezul magnetic al unui transformator variaza în raport cu frecventa si inductia de forma

Cum inductia magnetica B este proportionala cu fluxul F în miez, respectiv cu tensiunea electromotoare indusa, rezulta ca poate fi asociata dezvoltarii de putere activa, respectiv pierderilor în miez o rezistenta echivalenta pe baza relatiei

Completarea schemei echivalente din figura 3.19 pentru a considera si pierderile în miez presupune conectarea rezistentei R_m în paralel cu reactanta utila X_m, , fig. 3.20. Corespunzator acestei scheme, curentul I₁₀ absorbit de transformator la mersul în gol are o componenta reactiva de magnetizare I_10m si o componenta activa I_10a , corespunzatoare pierderilor în miez.

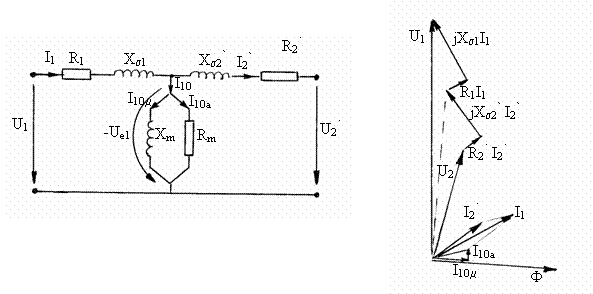
Fig. 3.20

3.3.4. Schema simplificata specifica functionarii în sarcina. Diagrama Kapp

Cu cât gradul de încarcare în sarcina al unui transformator este mai apropiat de sarcina nominala, inegalitatea I₁₀ << I este mai evidenta. Ca urmare, pentru analiza functionarii în sarcina este destul de potrivita schema electrica simplificata din figura 3.21, unde

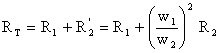
este rezistenta echivalenta a transformatorului, iar

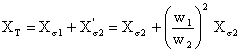
este reactanta echivalenta. Acestea sunt expresii ale parametrilor raportati la primar, care de multe ori se numesc rezistenta respectiv reactanta de scurtcircuit ale transformatorului. Diagrama de fazori pentru acest caz, fig. 3.22 este denumita diagrama Kapp.

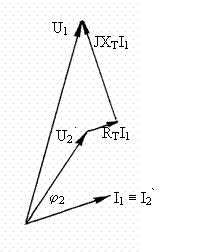
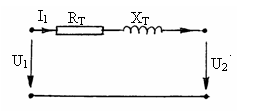
Fig. 3.21 Fig. 3.22

3.3.5. Aplicatie numerica

Un transformator monofazat având puterea nominala S_n 10 MVA si tensiunile nominale U_1n U_2n 35 kV absoarbe în gol curentul I₁₀ 10 A si puterea activa P₀ 22 kW. Atunci când secundarul este scurtcircuitat si este alimentat cu tensiunea U_1sc = 500V, transformatorul absoarbe curentul nominal si puterea activa P_sc = 75 kW. Presupunând ca cele doua înfasurari sunt caracterizate prin valori egale ale rezistentelor si reactantelor de dispersie, pentru secundar fiind vorba de valorile raportate la primar sa se determine valorile parametrilor schemei echivalente complete, care considera inclusiv pierderile în miez

Solutie

a)      Factorul de putere la functionarea în gol are valoarea

b)      Componentele activa si reactiva ale curentului de mers în gol sunt

c)      Curentul nominal primar al transformatorului are valoarea

d)      Factorul de putere la încercarea în scurtcircuit are valoarea

e)      Impedanta, rezistenta si reactanta echivalente de scurtcircuit ale transformatorului au valorile

f)        Parametrii transformatorului au valorile

Observatie privind importanta practica a raportarii circuitelor. Rezistentele si reactantele de scapari ale celor doua înfasurari primara si secundara au valori numerice cu atât mai diferite cu cât raportul de transformare w₁/w₂ are o valoare mai diferita de unitate. Practic, rapoartele R₁/R₂, X_s /X_s au aproximativ ordinul de marime al patratului raportului de transformare . Prin operatia de raportare, parametrii R₁ si pe de o parte si X_s si pe de alta parte au valori numerice aproximativ de acelasi ordin de marime.