11.1. Consideram spatiul vectorial euclidian ![]() (al vectorilor
(al vectorilor
![]() -dimensionali)
inzestrat cu o baza ortonormata
-dimensionali)
inzestrat cu o baza ortonormata ![]() asociat spatiului afin
asociat spatiului afin ![]() dimensional
dimensional
![]() (ale carui elemente sunt puncte) si in care s-a considerat un sistemul de coordonate carteziene format din punctul
(ale carui elemente sunt puncte) si in care s-a considerat un sistemul de coordonate carteziene format din punctul ![]() oarecare, dar fixat si baza ortonormala
oarecare, dar fixat si baza ortonormala ![]() ),
notat
),
notat ![]() .
.
Fie ![]() un
punct oarecare al spatiului afin
un
punct oarecare al spatiului afin ![]() .
Vectorul
.
Vectorul
![]() , (1)
, (1)
se numeste vectorul
de pozitie al punctului ![]() ,
iar componentele
,
iar componentele ![]() ale vectorului
ale vectorului ![]() pe baza
pe baza ![]() se numesc coordonatele
punctului
se numesc coordonatele
punctului ![]() in sistemul de coordonate carteziene ales
in sistemul de coordonate carteziene ales ![]() .
.
Corespondenta intre punctele ![]() si
si ![]() -uplele
ordonate de numere reale
-uplele
ordonate de numere reale ![]() este biunivoca pentru un sistem de coordonate
este biunivoca pentru un sistem de coordonate ![]() dat si notam aceasta corespondenta prin
dat si notam aceasta corespondenta prin ![]() .
Pentru sistemul de coordonate dat folosim notatia
.
Pentru sistemul de coordonate dat folosim notatia ![]() .
.
Fie ![]() un alt spatiu vectorial euclidian, de aceeasi dimensiune, raportat la o baza
ortonormala in care s-a considerat un alt sistem de coordonate carteziene
un alt spatiu vectorial euclidian, de aceeasi dimensiune, raportat la o baza
ortonormala in care s-a considerat un alt sistem de coordonate carteziene ![]() .
.
Presupunem ca s-a definit un omeomorfism
(corespondenta biunivoca si continua) intre domeniile ![]() si
si ![]() .
.
Coordonatele carteziene ![]() ale punctului
ale punctului ![]() care este imaginea lui
care este imaginea lui ![]() prin omeomorfismul dat, se numesc coordonate curbilinii ale lui
prin omeomorfismul dat, se numesc coordonate curbilinii ale lui ![]() .
Intre coordonatele carteziene ale punctului
.
Intre coordonatele carteziene ale punctului ![]() si coordonatele carteziene ale punctului
si coordonatele carteziene ale punctului ![]() ,
evident, s-au stabilit relatiile
,
evident, s-au stabilit relatiile
![]() , (2)
, (2)
definite cu ajutorul a ![]() -functii
inversabile
-functii
inversabile ![]() ,
,
![]() (deocamdata
numai continue).
(deocamdata
numai continue).
Relatiile date de transformata inversa au forma
![]() , (3)
, (3)
unde ![]() ,
,
![]() sunt
functii continue.
sunt
functii continue.
![]()
11.3. Observatie.
(a). Fie suprafata deschisa ![]() din
din ![]() ,
marginita de curba
,
marginita de curba ![]() .
Presupunem ca s-a stabilit un omeomorfism intre punctele suprafetei
.
Presupunem ca s-a stabilit un omeomorfism intre punctele suprafetei ![]() si un anumit domeniu plan
si un anumit domeniu plan ![]() din
din ![]() (vezi, fig.1).
(vezi, fig.1).
Coordonatele carteziene ![]() ale punctelor de pe suprafata
ale punctelor de pe suprafata ![]() sunt legate de coordonatele carteziene
sunt legate de coordonatele carteziene ![]() ale unui punct din
ale unui punct din ![]() prin formulele
prin formulele
![]() , (4)
, (4)
unde functiile ![]() sunt presupuse de clasa
sunt presupuse de clasa ![]() .
Perechile
.
Perechile ![]() definesc coordonatele
curbilinii pe suprafata
definesc coordonatele
curbilinii pe suprafata ![]() .
.
|
Figura 1. Coordonate curbilinii pe suprafata |
(b). Consideram in spatiul vectorial
euclidian ![]() curbele deschise
curbele deschise ![]() care sunt omeomorfe cu anumite intervale
care sunt omeomorfe cu anumite intervale ![]() ale axei reale
ale axei reale ![]() .
.
Coordonatele carteziene ![]() ale punctelor de pe curba
ale punctelor de pe curba ![]() sunt legate de coordonata carteziana
sunt legate de coordonata carteziana ![]() a unui punct din
a unui punct din ![]() ,
prin formulele
,
prin formulele
unde functiile ![]() sunt de clasa
sunt de clasa ![]() .
Parametrul
.
Parametrul ![]() defineste coordonata
curbilinie pe curba
defineste coordonata
curbilinie pe curba ![]() .
.
11.4. Observatie.
In general, daca dorim sa punem o problema asemanatoare cu cea din observatia 11.3
in cazul unei suprafete inchisa ![]() din
din ![]() ,
vom constata ca nu este posibil de rezolvat. Asadar, o astfel de reprezentare globala, in general, este
imposibila. De exemplu, consideram sfera
,
vom constata ca nu este posibil de rezolvat. Asadar, o astfel de reprezentare globala, in general, este
imposibila. De exemplu, consideram sfera
Fie ![]() si
si ![]() ,
coordonatele curbilinii ale punctului
,
coordonatele curbilinii ale punctului ![]() de pe sfera
de pe sfera ![]() .
Legatura dintre coordonatele carteziene
.
Legatura dintre coordonatele carteziene ![]() si coordonatele curbilinii
si coordonatele curbilinii ![]() este data de relatiile:
este data de relatiile:
![]() (7)
(7)
Relatiile (7) realizeaza un omeomorfism intre o
portiune a sferei si un anumit domeniu plan al coordonatelor ![]() ,
cu conditia ca portiunea de pe sfera sa nu contina nici unul dintre polii
,
cu conditia ca portiunea de pe sfera sa nu contina nici unul dintre polii ![]() si
si ![]() .
.
Polului
![]() ii corespunde coordonatele curbilinii
ii corespunde coordonatele curbilinii ![]() si
si ![]() oarecare in
oarecare in ![]() ,
iar polului
,
iar polului ![]() ii corespunde coordonatele curbilinii
ii corespunde coordonatele curbilinii ![]() si
si ![]() oarecare in
oarecare in ![]() .
.
11.5. Observatie.
Daca corespondenta dintre domeniile ![]() si
si ![]() este realizata de un difeomorfism de clasa
este realizata de un difeomorfism de clasa ![]() ,
,
![]() ,
, ![]() ,
,
atunci spunem ca s-a
realizat o transformare regulata a
domeniului ![]() in
in ![]() .
.
(Spunem ca functia ![]() este difeomorfism de clasa
este difeomorfism de clasa ![]() daca
daca
![]() este bijectiva (admite o unica inversa
este bijectiva (admite o unica inversa ![]() )
si functiile
)
si functiile ![]() sunt
de clasa
sunt
de clasa ![]() ).
).
![]() , (9)
, (9)
unde,
functia vectoriala ![]() este presupusa de clasa
este presupusa de clasa ![]() pe un anumit domeniul
pe un anumit domeniul ![]() ( daca si numai daca functiile coordonate
( daca si numai daca functiile coordonate ![]() ,
sunt de clasa
,
sunt de clasa ![]() pe
pe ![]() )
si astfel incat jacobianul (determinantul functional) transformarii
(9) este nenul in
)
si astfel incat jacobianul (determinantul functional) transformarii
(9) este nenul in ![]() (pastreaza semn constant in
(pastreaza semn constant in ![]() ),
adica
),
adica
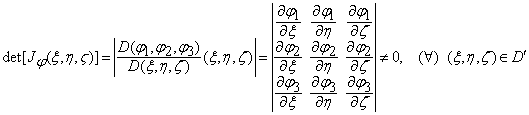 . (10)
. (10)
![]() , (11)
, (11)
este de clasa ![]() pe
pe ![]() .
.
![]()
Figura 2. Coordonate curbilinii in spatiu
formeaza o baza ortonormata in orice punct ![]() ,
adica
,
adica
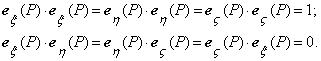 (17)
(17)
si ca ![]() formeaza un triedru orientat drept.
formeaza un triedru orientat drept.
![]() . (20)
. (20)
Figura 3. Elementul de volum in coordonate curbilinii
![]() (21)
(21)
sau inca, folosind relatiile (14) deducem
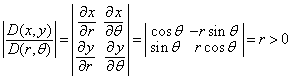 . (24)
. (24)
Figura.4. Coordonate polare
![]() , (25)
, (25)
avem,
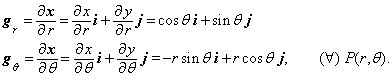 (26)
(26)
 , (28)
, (28)
sunt marimile
vectorilor ![]() si
si ![]() ,
denumiti coeficientii lui Lamé.
,
denumiti coeficientii lui Lamé.
![]()
![]() . (31)
. (31)
Figura 5. Coordonate cilindrice.
sunt coeficientii
lui Lamé, ce reprezinta marimile vectorilor ![]() .
.
![]() . (37)
. (37)
![]() . (38)
. (38)
Figura 6. Coordonate sferice.
![]() , (41)
, (41)
avem
 (43)
(43)
unde
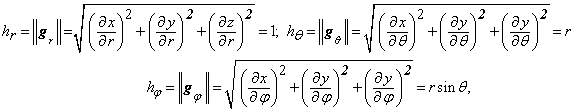 (44)
(44)
sunt coeficientii lui Lamé, ce reprezinta
marimile vectorilor ![]() .
.
![]() un domeniu din spatiul euclidian punctual
tridimensional
un domeniu din spatiul euclidian punctual
tridimensional ![]()
![]() un reper cartezian ortogonal asociat acestui spatiu
punctual, iar V multimea vectorilor
liberi asociati lui
un reper cartezian ortogonal asociat acestui spatiu
punctual, iar V multimea vectorilor
liberi asociati lui ![]() , organizata ca spatiu vectorial peste corpul
numerelor reale. Notam cu
, organizata ca spatiu vectorial peste corpul
numerelor reale. Notam cu ![]() o baza a spatiului vectorial asociat V,
iar cu
o baza a spatiului vectorial asociat V,
iar cu ![]() coordonatele unui punct oarecare
coordonatele unui punct oarecare ![]() in reperul
considerat.
in reperul
considerat.
![]() , definite punctual pe D se numesc campuri
(altfel spus, fiecarui punct P al
spatiului D ii asociem scalarul sau
vectorul
, definite punctual pe D se numesc campuri
(altfel spus, fiecarui punct P al
spatiului D ii asociem scalarul sau
vectorul ![]() , bine determinat). Aceste campuri sunt independente
de timpul t si de aceea se numesc campuri stationare sau permanente, iar cand functiile care
definesc campurile respective depind si de timpul t deci,
, bine determinat). Aceste campuri sunt independente
de timpul t si de aceea se numesc campuri stationare sau permanente, iar cand functiile care
definesc campurile respective depind si de timpul t deci, ![]() , atunci campurile se numesc nestationare sau nepermanente
(sau variabile).
, atunci campurile se numesc nestationare sau nepermanente
(sau variabile).
![]() care asociaza
la orice punct
care asociaza
la orice punct![]() , numarul real
, numarul real ![]()
![]() din spatiu
(denumit camp potential) definit prin
din spatiu
(denumit camp potential) definit prin
![]()
 unde
unde ![]()
![]()
![]() si
si ![]() un punct fixat
din D. Suprafata de ecuatie
un punct fixat
din D. Suprafata de ecuatie
![]() (1)
(1)
![]() ce trece prin
punctul fix
ce trece prin
punctul fix ![]() . Ecuatia (1) se poate scrie sub forma
. Ecuatia (1) se poate scrie sub forma
![]() (2)
(2)
![]() are ecuatia
are ecuatia
![]()
![]()
Figura 1. Suprafete de nivel,
si gradientul in punctul P.
![]() se numesc linii de nivel. De exemplu, pe o harta
liniile de egala altitudine; aceste linii sunt numite si curbe de nivel.
se numesc linii de nivel. De exemplu, pe o harta
liniile de egala altitudine; aceste linii sunt numite si curbe de nivel.
![]() si punctul
fixat
si punctul
fixat ![]() , iar
, iar ![]() un punct
variabil din D situat pe dreapta ce
trece prin P si care are directia
determinata de versorul
un punct
variabil din D situat pe dreapta ce
trece prin P si care are directia
determinata de versorul ![]() (vezi fig. 2).
(vezi fig. 2).
Vom nota cu ![]() si
si ![]() vectorii de
pozitie ai punctelor P respectiv
vectorii de
pozitie ai punctelor P respectiv![]() . Atunci avem
. Atunci avem ![]()
![]() Figura 2. Derivata dupa directia
Figura 2. Derivata dupa directia![]()
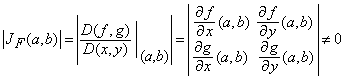
Transformata ![]() se numeste transformata regulata pe
se numeste transformata regulata pe ![]() daca este transformata regulata in orice punct
daca este transformata regulata in orice punct
![]() .
.
Vom
observa ca daca ![]() este transformare regulata in punctul
este transformare regulata in punctul ![]() ,
atunci
,
atunci ![]() este transformare regulata intr-o intreaga
vecinatate a punctului
este transformare regulata intr-o intreaga
vecinatate a punctului![]() .
Intr-adevar, deoarece
.
Intr-adevar, deoarece ![]() intr-o vecinatate
intr-o vecinatate ![]() a punctului
a punctului ![]() ,
atunci jacobianul este functie continua in
,
atunci jacobianul este functie continua in ![]() si diferit de zero in acest punct; deci exista
o vecinatate
si diferit de zero in acest punct; deci exista
o vecinatate ![]() a punctului
a punctului ![]() pe care jacobianul este nenul in vecinatatea
pe care jacobianul este nenul in vecinatatea ![]() a lui
a lui ![]() .
Asadar, in vecinatatea
.
Asadar, in vecinatatea ![]() avem
avem ![]() si jacobianul este nenul, deci
si jacobianul este nenul, deci ![]() este transformare regulata in
este transformare regulata in ![]() .
.
13.4. Propozitie. Jacobianul unei transformari regulate in domeniul ![]() pastreaza acelasi semn in orice punct
pastreaza acelasi semn in orice punct ![]() .
.
Demonstratie.
Deoarece transformarea este regulata pe domeniul ![]() (multime conexa
si deschisa), atunci jacobianul
transformarii este functie continua pe
(multime conexa
si deschisa), atunci jacobianul
transformarii este functie continua pe ![]() .
Daca jacobianul ar lua valori de semne diferite in doua puncte distincte din
.
Daca jacobianul ar lua valori de semne diferite in doua puncte distincte din ![]() ,
atunci exista un punct
,
atunci exista un punct ![]() a.i.
a.i. ![]() ceea ce ar contrazice ipoteza ca transformarea
este regulata in
ceea ce ar contrazice ipoteza ca transformarea
este regulata in ![]() .
.
Exemplul 1. Fie ![]() si functiile
si functiile ![]()
![]()
![]()
Vom arata ca relatiile ![]() asociaza la orice punct
asociaza la orice punct ![]() un unic punct
un unic punct ![]() unde
unde
![]()
(i). Multimile ![]() si
si ![]() sunt deschise si conexe (domenii plane).
Definim functia
sunt deschise si conexe (domenii plane).
Definim functia ![]() .
Se verifica usor ca
.
Se verifica usor ca ![]() .
.
|
Figura 7. Transformarea regulata (*) a domeniului |
(ii).
Jacobianul transformarii ![]() este nenul in fiecare punct din
este nenul in fiecare punct din ![]() (
(![]() este o transformare regulata) :
este o transformare regulata) :
![]()
Inversa transformarii ![]() ,
,
![]() ,
are forma
,
are forma
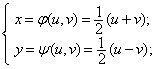
si jacobianul transformarii inverse are valoarea
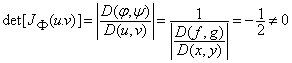 in orice
punct din
in orice
punct din ![]() .
.
Exemplul 2. Transformarea de coordonate polare in plan
![]() ,
,
![]() ,
, ![]()
defineste functia vectoriala ![]() ,
,
![]() ,
care are jacobianul nenul,
,
care are jacobianul nenul,
![]()
Se observa ca jacobianul acestei transformari este nenul in toate punctele din spatiul euclidian bidimensional cu exceptia originii. Deci transformarea este regulata in orice domeniu din plan care nu contine originea. Originea este punct de neregularitate impus de alegerea coordonatelor polare.
Inversa transformarii ![]() ,
definita de functiile coordonate
,
definita de functiile coordonate
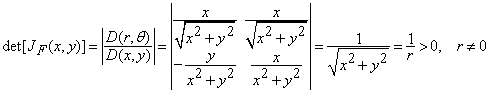
|
Figura 8. Transformarea de coordonatelor polare |
Functia ![]() ,
definita de relatiile
,
definita de relatiile ![]() ,
deoarece are jacobianul pozitiv pentru
,
deoarece are jacobianul pozitiv pentru ![]() realizeaza o transformare regulata a multimii
realizeaza o transformare regulata a multimii ![]() pe multimea
pe multimea ![]() .
.
13.5. Teorema. Fie ![]() ,
multimi deschise. Daca transformarea
,
multimi deschise. Daca transformarea ![]() ,
definita prin
,
definita prin
Demonstratie. Fie ![]() si
si ![]() ,
,
![]() .
Aceste relatii sugereaza introducerea
functiilor
.
Aceste relatii sugereaza introducerea
functiilor ![]() , definite prin
, definite prin
![]() . (3)
. (3)
Vom arata ca functia vectoriala ![]() verifica conditiile pentru ca ecuatia
verifica conditiile pentru ca ecuatia 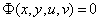 sa poata fi rezolvata in raport cu
sa poata fi rezolvata in raport cu ![]() ,
adica putem determina
,
adica putem determina ![]() ca functii de variabilele
ca functii de variabilele ![]() astfel ca
astfel ca ![]() .
.
Prin ipoteza, avem
![]() (4)
(4)
Deoarece ![]() atunci
exista o vecinatate
atunci
exista o vecinatate ![]() a.i
a.i ![]() .
Potrivit relatiilor (3) rezulta ca functiile
.
Potrivit relatiilor (3) rezulta ca functiile ![]() sunt de clasa
sunt de clasa ![]() (chiar de clasa
(chiar de clasa ![]() ,
unde
,
unde ![]() )
si avem
)
si avem
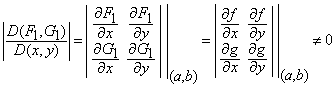
Atunci, din teorema functiilor implicite, rezulta ca
exista vecinatatile ![]() si
si ![]() si functiile
si functiile ![]() a.i.
a.i. ![]() ,
oricare ar fi
,
oricare ar fi ![]() si care verifice identitatile
si care verifice identitatile
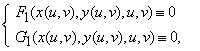 oricare
ar fi
oricare
ar fi ![]() , (5)
, (5)
Pentru a deduce relatia (6) vom arata ca intre
jacobianul transformarii date ![]() si jacobianul transformarii inverse
si jacobianul transformarii inverse ![]() exista relatia
exista relatia ![]() .
.
In adevar, deoarece relatiile ![]() si
si ![]() sunt verificate
sunt verificate ![]() ,
avem
,
avem
![]() si
si ![]() .
.
Sistemul (5) este echivalent cu sistemul
![]() oricare ar fi
oricare ar fi ![]() .
.
Diferentiind aceste relatii si folosind expresiile
![]() si
si ![]() ,
,
deducem
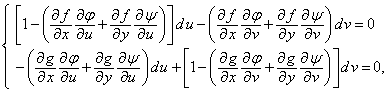 oricare ar fi
oricare ar fi ![]() si
si ![]() .
.
Acest sistem poate fi scris sub forma
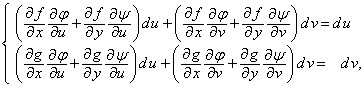 oricare ar fi
oricare ar fi ![]() si
si ![]() .
.
sau, folosind scrierea matriciala, avem
 oricare ar fi
oricare ar fi ![]() si
si ![]() .
.
Asadar, rezulta
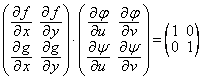
de unde, luand determinantul in ultima relatie, obtinem (6).
|